Izračun vektorja uravnoteženja, primeri, vaje

On uravnoteženje vektorja To je tisti, ki nasprotuje nastalemu vektorju in je zato sposoben uravnotežiti sistem, saj ima enako velikost in isto smer, vendar v nasprotju s tem.

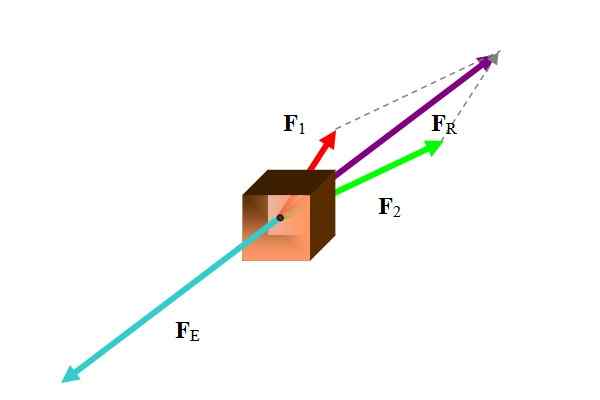
Večkrat se izravnalni vektor nanaša na vektor sile. Za izračun izravnalne sile je najprej nastala sila, kot je prikazano na naslednji sliki:

Slika 1. Na telesu sta dve sili, katerih rezultat je uravnotežen s silo v turkizni barvi. Vir: Self Made.

Obstajajo različne metode za opravljanje te naloge v skladu s podatki. Ker so sile vektorji, je rezultat vektorska vsota sodelujočih sil:

F_R = F₁ + F₂ + F₃ +  .. .

Med metodami, ki jih je treba uporabljati. V primeru je bila uporabljena slika paralelogramska metoda.

Ko najdete nastalo silo, je ravnotežna sila ravno nasprotna vektor.

Ja F_In To je uravnotežena sila, potem je izpolnjena F_In Uporablja se na določeni točki, zagotavlja ravnovesje prevoda sistema. Če gre za en sam delček, se ne bo premaknil (ali pa ga morda počne s konstantno hitrostjo), če pa gre za podaljšan predmet, bo še vedno imel možnost obračanja:

F_R + F_In = 0

[TOC]

Primeri

Na vseh straneh so prisotne sile. Sami smo uravnoteženi s silo, ki jo stol izvaja za kompenzacijo teže. Predmeti, ki jih najdemo v mirovanju: knjige, pohištvo, stropne svetilke in veliko število mehanizmov, sile nenehno uravnotežijo.

Vam lahko služi: neelastični udarci: v dimenziji in primerih

Na primer, knjigo za počitek na mizi je uravnotežena z normalno silo, ki jo izvaja na knjigi, kar preprečuje, da bi padel. Enako velja za verigo ali kabel, ki drži svetilko, ki visi s stropa v sobi. Kabli, ki zadržujejo obremenitev.

V tekočini lahko nekateri predmeti plavajo in ostanejo v mirovanju, saj njihova teža uravnoteži naraščajoča sila, ki jo izvaja tekočina, imenovana pritisk.

Različni mehanizmi je treba uravnotežiti, če poznate vektor izravnalne sile, kot so palice, tramovi in ​​stebri.

Pri uporabi ravnotežja je treba nekako uravnotežiti težo predmeta s silo, ki je enakovredna, bodisi z dodajanjem uteži ali z vzmeti.

Tabela sil

Tabela sil se uporablja v laboratoriju za določitev uravnotežene sile. Sestavljen je iz krožne platforme, od katere imate zgornji pogled na sliki, ki ima transporter za merjenje kotov.

Na robovih mize so škripci, skozi katere strune, ki držijo uteži, in ki se zbližajo v obročku, ki je v središču.

Na primer obe uteži sta obešeni. Napetosti, ustvarjene na strunah s temi utežmi, so na sliki 2 narisane v rdeči in modri barvi. Tretja tehta zeleno, lahko uravnoteži nastalo silo drugih dveh in sistem ohranja v ravnovesju.

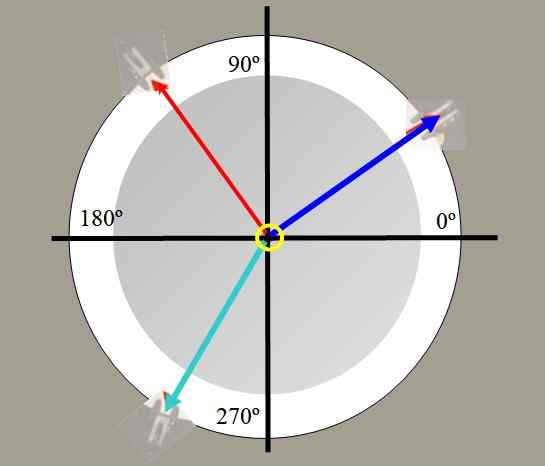Slika 2. Pogled z vrha tabele sil. Vir: Self Made.

S tabelo sil lahko preverite vektorski značaj sil, razgradite sile, poiščete ravnotežno silo in preverite Lamyjev izrek:

Vam lahko služi: sonce

Če Telo je v ravnotežju zahvaljujoč trem koplanarnim, sočasnim in nekolinealnim (ne -palelskim) silam, imenovanim Do, B in C, Razmerje med temi silami je naslednje:

A/ sin α = b/ sen β = c/ sen γ

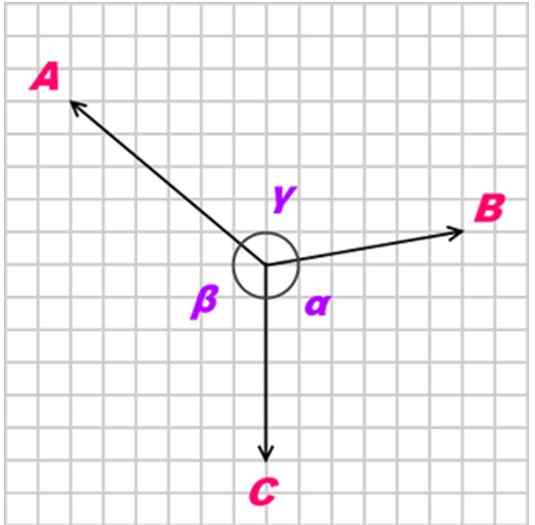Slika 3. Lamyjev teorem velja za sočasne in koplanarne sile. Vir: Wikimedia Commons.

Rešene vaje

-Vaja 1

V tabeli sil na sliki 2 tehtajo 225 g (modra napetost) in 150 g (rdeča napetost), z prikazanimi koti. Poiščite vrednost izravnalne sile in kota, ki ga ta oblika z navpično osi.

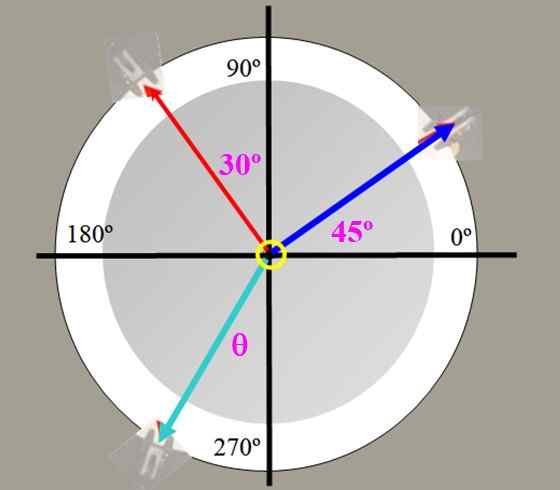Slika 4. Prisili tabelo za vajo 1.

Rešitev

Težavo je mogoče obnašati z utežmi, izraženimi v gramih (silah). Naj p₁ = 150 gramov in P₂ = 225 gramov, ustrezne komponente so:

Str_1x = 225 . cos 45 ° g = 159.10 g; Str_1y = 225 . cos 45 ° g = 159.10 g

Str_2x = -150 . Sen 30 ° G = -75.00 g; Str_{2 in} = 150 . Cos 30 ° g = 129.90 g

Nastala teža Str_R Komponente algebraično dodajajo:

Str_Rx = 159.10 - 75.00 g = 84.10 g

Str_Ry = 159.10 + 129.90 g = 289.00 g

Uravnotežna teža Str_In je nasprotni vektor Str_R:

Str_Ex = -84.10 g

Str_zdravo = -289.00 g

Obseg uravnoteženja se izračuna z:

Str_In = (Str_Ex² + Str_zdravo²)^1/2 = (-84.10)² + (-289.00)²)^1/2 G = 301 g

Kot θ slike je:

θ = arctg (-84.10 / -289.00) = 16.2. glede na osi in negativno.

-Vaja 2

Poiščite izravnalni vektor sistema, prikazan na sliki, vedoč, da vsak kvadrat meri 10 m strani.

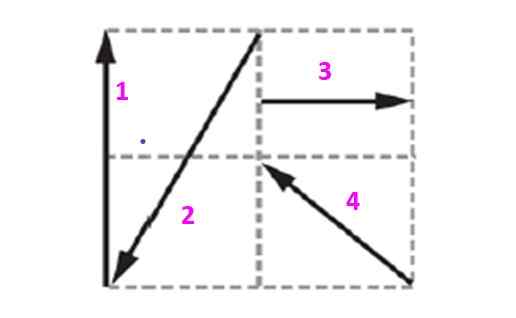Slika 5. Diagram za primer rešenega 2.

Rešitev

Vektorji, vsebovani v tej mreži, bodo izraženi v enoti in pravokotni vektorji Yo in J ki določajo ravnino. Vector 1, ki bo označen kot v₁ Ima 20 m velikost in je usmerjen navpično navzgor. Lahko se izrazi kot:

Lahko vam služi: sevalni prenos toplote (s primeri)

v₁ = 0 Yo +dvajset J m

Iz risbe je razvidno, da je Vector 2:

v₂ = -10 Yo - dvajset J m

Vektor 3 je vodoraven in točke v pozitivnem naslovu:

v₃ = 10 Yo + 0 J  m

Končno je Vector 4 nagnjen 45 °, saj je diagonala kvadrata, zato njene komponente merijo enako:

v₄ = -10 Yo + 10 J m

Upoštevajte, da znak -.

Nastali vektor dobimo z dodajanjem komponente komponente:

v_R = -10 Yo + 10 J m

Potem je izravnalni vektor sistema:

v_In = 10 Yo - 10 J m

Reference

1. Beardon, t. 2011. Uvod v vektorje. Okreval od: nrich.Matematika.org.
2. Bedford, 2000. Do. Mehanika za inženiring: statična. Addison Wesley. 38-52.
3. Figueroa, d. Serija: Fizika za znanost in inženiring. Zvezek 1. Kinematika.31-68.
4. Fizično. Modul 8: Vektorji. Okrevano od: FRTL.UTN.Edu.ar
5. Hibbeler, R. 2006. Mehanika za inženirje. Statična. 6. izdaja. Continental uredništvo. 15-53.
6. Dodatni kalkulator vektor. Okrevano od: 1728.org
7. Vektorji. Okreval od: wikibooks.org