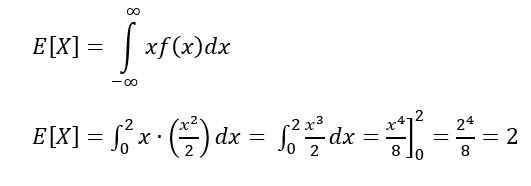Neprekinjena naključna spremenljivka

Pojasnjujemo, kakšna je neprekinjena naključna spremenljivka, njegove značilnosti, primeri in rešena vaja je

Kaj je neprekinjena naključna spremenljivka?

A Neprekinjena naključna spremenljivka To je numerična vrednost, ki jo dobimo naključno, kar je posledica poskusa in lahko vzame neskončne vrednosti. To pomeni, da je, znani dve zaporedni vrednosti spremenljivke, vedno mogoče najti drugo vmesno vrednost med njimi.

Z neskončno količino vrednosti zbirka neprekinjenih spremenljivih vrednosti ni obračunavanje in skoraj vedno pripada naboru resničnih številk.

Primeri te vrste spremenljivk so stas, teža in telesna temperatura osebe, vendar jih je mogoče določiti nešteto, spodaj pa bomo našli več primerov. V nasprotju z neprekinjeno naključno spremenljivko obstaja diskretna naključna spremenljivka, ki je računovodstvo, na primer število hčera v družini ali koliko avtomobilov proda agencija po enem mesecu.

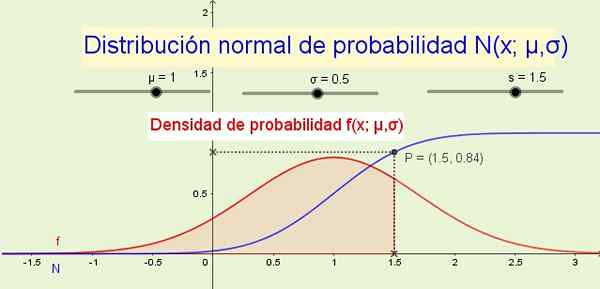
Diskretne naključne spremenljivke pogosto sledijo normalni porazdelitvi verjetnosti. Vir: f. Zapata.

Neprekinjena naključna spremenljivka je označena s kapitalsko črko, kot je X, in neskončne vrednosti, ki jih spremenljivka vzame, so možni rezultati naključnega poskusa:

X = x₁, x₂, x₃,… ∞

Vsaka vrednost ima določeno verjetnost pojavljanja in do modela, s katerim se izračuna ta verjetnost, se imenuje Porazdelitev verjetnosti.

Ker pa X sprejme neskončne vrednosti, verjetnosti za posebne vrednosti spremenljivke ni mogoče izračunati. Torej je treba določiti funkcijo f (x), imenovano Akumulirana funkcija distribucije, ali preprosto distribucijsko funkcijo, v skladu s katero se nakopičena verjetnost izračuna na določeno vrednost ali med dvema vrednostma:

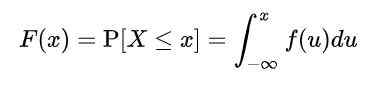
Kje f (u) Prejmite ime Funkcija gostote. Definirano na ta način, F (x) predstavlja verjetnost, da X je med -∞ in x.

Značilnosti neprekinjene naključne spremenljivke

Neprekinjene naključne spremenljivke so popolne f (x).

Funkcija gostote f (x) mora izpolniti naslednje lastnosti:

• Funkcija f (x) Je pozitivno: f (x)> = 0
• Območje pod krivuljo y = f (x) Vedno je enak 1, to pomeni, da je verjetnost pojavljanja nekaterih rezultatov x V intervalu je (-∞, +∞) 100%.
• Verjetnost, da je X v intervalu [a, b], se izračuna z naslednjim definiranim integralom:

Vam lahko služi: curtoza: definicija, vrste, formule, za kaj je na primer

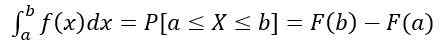
Ki je enakovredno območju pod krivuljo y = f (x), razumljeno med do in b. Poleg:

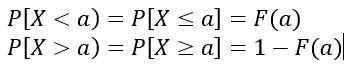
Vrednosti f (x) Ne predstavljajo verjetnosti, torej P [x = c] = 0. Ustrezne vrednosti so tiste, ki ustrezajo območju pod krivuljo y = f (x), ki predstavljajo verjetnost.

• Z izpeljavo funkcije distribucije F (x) s spoštovanjem do x, dobimo f (x).

Graf f (x) Za neprekinjeno naključno spremenljivko je analogen frekvenčnemu poligonu, ki je zgrajen za diskretno statistično spremenljivko, z razliko, da za naključno spremenljivko širina intervala postane neskončno majhna.

Upanje

Upanje je eden značilnih ukrepov neprekinjene spremenljivke. Upanje ali pričakovana vrednost X Označuje vrednost, ki se pričakuje pogosteje in se izračuna z naslednjim integralom:

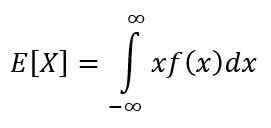
Njene lastnosti so:

• E [a∙ x] = a∙ e [x]
• E [x + y] = e [x] + e [y]]
• E [a∙ x+b∙ y] = a∙ e [x] + b∙ e [y]

Kjer koli zneske do in b So resnične številke.

Primeri

Kot je bilo že omenjeno, obstaja veliko situacij, v katerih je mogoče določiti eno ali več neprekinjenih naključnih spremenljivk. Na znanosti in drugih področjih so najpogostejši čas, dolžina, teža, volumen in temperatura:

Čas

Za optimizacijo procesov in storitev so zasnovani poskusi, ki preučujejo čas, ki ga potrebujejo za izvedbo:

X = čas, ki stranko pripelje v okno banke.

Y = kaj je potrebno pri hitri hrani pri postrežbi.

Z = čas, v katerem pride do določene kemijske reakcije.

Stature in uteži

V mnogih študijah o ljudeh in živalih so stature in uteži pomembni:

X = višina deklet na 6. tečaju. Diplomirala v vsaki šoli v mestu.

Vam lahko služi: skladnost: skladne številke, merila, primeri, vaje

Y = teža dojenčkov ob rojstvu v javni bolnišnici.

Z = teža krav na kmetiji.

Temperature

Temperatura je ustrezen parameter v številnih kemijskih procesih, ki v določenem območju običajno vzamejo neskončne vrednosti:

X = temperatura, pri kateri pride do določene kemične reakcije, vedoč, da se to zgodi med 80 ° C in 120 ° C.

Rešene vaje

Vaja 1

Določite, kakšne so neprekinjene naključne spremenljivke:

1. Število študentov, ki obiskujejo kavo univerze.
2. Krvni tlak bolnikov, ki pridejo na urgenco.
3. Dolžina ptičjih kril, ogrožene vrste, ki naseljujejo rezervat.
4. Čas med eno osebo in drugo se obravnava v banki.
5. Znesek pomanjkljivih izdelkov na mesec v tovarni.
6. Ravni holesterola v piščancih kmetije.
7. Količina uličnih svetilk na ulici, skupno 12.

Rešitev

1.- Število študentov, ki se jih udeležijo dneva, je otrplo, zato ta spremenljivka ni neprekinjena, ampak diskretna.

2.- Je neprekinjeno. Krvni tlak bolnikov lahko v določenem območju prevzame katero koli vrednost.

3.- Neprekinjena spremenljivka, saj dolžina krila ptice prevzame katero koli vrednost med minimalno in največ, odvisno od vrste.

4.- Čas med storitvijo za stranke je spremenljiv in lahko v določenem območju vzame katero koli vrednost, na primer med 1 in 5 minutami.

5.- Ker je število pokvarjenih izdelkov računovodstvo, je diskretna naključna spremenljivka.

6.- Ta spremenljivka je neprekinjena, saj raven holesterola v piščancih prevzame kakršno koli vrednost v predhodno določenem območju.

Vam lahko služi: komplementarni koti: Kateri in kako se izračunajo, primeri, vaje

7.- Diskretno. Število lučk osvetlitve, ki deluje.

Vaja 2

Določena je neprekinjena naključna spremenljivka X = "Raven holesterola " V določeni raznolikosti piščancev na kmetiji, ki ima naslednjo funkcijo gostote f (x):

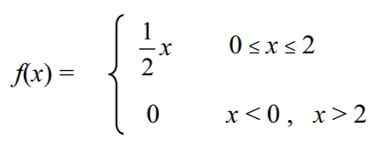
Izračunajte naslednje:

1. F (x)
2. P [x ≤2]
3. Upanje Ex]

Rešitev

V skladu z definicijo, podano na začetku:

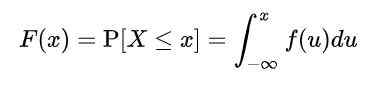
Zato, F (x) Je funkcija v delih. Za interval x<0, F (x) Je enak 0, za lastnosti, navedene na začetku.

V intervalu 0≤x≤2, Nedefinični integral je razrešen:

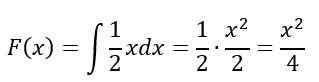
Končno za interval x> 2, F (x) = 1, po lastnostih, F (x) Ostaja takole:

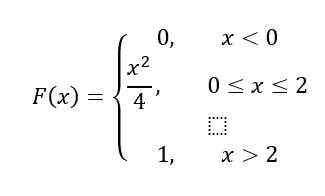
Rešitev b

Iskana verjetnost je F (1.2) in como x = 1.2 Najdeno je med 0≤x≤2, tisti del F (x) Za oceno:

F (1.2) = ¼ ∙ (1.2)² = 0.36.

Rešitev c

Za izračun upanja ali pričakovane vrednosti se uporablja: