Relativna vrednost

Kakšna je relativna vrednost številke?

On relativna vrednost številke O DECIMAL SISTEMSKI ŠTEVILNA je odvisna od položaja, ki ga zaseda, ko je del slike. Zato se reče, da gre za pozicijsko vrednost. Zelo preprost primer: Relativna vrednost 1 V številki 123, Bo 100, Ker 1 zaseda položaj stotine.

Še en primer: Številka 58 tvori števke 5 in 8. Preučitev te številke od desne proti levi je relativna vrednost 8 8, saj je v položaju enot in relativna vrednost 5 je 50, za zasedbo mesta desetin. Številka se bere "Petdeset -vih".

Po drugi strani imajo iste števke v številki 85 različne relativne vrednosti, saj so si izmenjali položaje. Vedno se začne od desne do leve, relativna vrednost 5 v tem primeru je 5, relativna vrednost 8 je 80, število pa se bere "osemdeset -pet".

Kako najti relativno vrednost številke?

Splošni postopek za iskanje relativne vrednosti vsake številke je naslednji:

• Prva številka od desne do leve je v položaju enot in njihova vrednost se pomnoži z 1.
• Naslednja številka ustreza desetinom in se pomnoži z 10.
• Naslednji položaj ustreza stotine in vrednost številke se pomnoži s 100.
• Naslednji položaj je tisoč, zato je številka pomnožena s 1000.

In tako naprej za večje številke, pomnožite številko z ustreznimi 10 moči: 100000, 100000 in več.

Na primer, številko 321 lahko zapišemo kot 3*100 + 2*10 + 1*1 ali enakovredno 300 + 20 + 1. V prejšnjem primeru je hitro razvidno, da je relativna vrednost 3 300, 2 je 20 in 1 je 1.

Vam lahko služi: distribucijska lastnina

Primeri relativnih vrednosti

Številka 727

Če želite določiti relativno vrednost številke, morate voditi naslednje osnovno načelo pisnega oštevilčenja decimalnega sistema:

Vsaka številka na levi strani predstavlja enoto 10 -krat višje in obratno: Vsaka številka desno od drugega predstavlja enoto 10 -krat manjšo. 

Na primer, 727 figura, ki se glasi "sedemsto sedemindvajsetih", je sestavljena iz števk 2 in 7, pri čemer 7 ponavljajoči se, vendar zaseda različne položaje.

Branje 727 Od desne proti levi je opaziti, da 7 na desni zavzema položaj enote, zato se pomnoži z 1:

7 x 1 = 7

In njegova relativna vrednost je 7.

Število 2 na sredini zaseda položaj desetin in za iskanje njihove relativne vrednosti se pomnoži z 10:

2 x 10 = 20

Končno ima 7 do skrajne levice položaj na stotine. Potem se morate pomnožiti s 100 in njegova relativna vrednost je:

7 x 100 = 700

Upoštevajte, da je samo, če številka zaseda položaj enote, da sta njegova absolutna vrednost in njegova relativna vrednost enaka. Če je torej relativna vrednost številke VR in je njegova absolutna vrednost VA, je splošna formula za iskanje relativne vrednosti:

VR = absolutna vrednost VA × vrednost njegovega položaja

Slika lahko zapišemo kot vsoto relativnih vrednosti njegovih števk, to je znano kot razvit zapis. Nadaljevanje s primerom številke 727 morate:

727 = 700 + 20 + 7

In če raje uporabljate moči 10, je tudi številka 727 izražena enakovredna kot:

727 = 7 ∙ 10² + 2 ∙ 10¹ + 7 ∙ 10⁰

Lahko vam služi: večkratniki 8: kaj so in razlaga

Kjer eksponenti moči, ki temelji na 10, predstavljajo položaj vsake številke in se imenujejo Indeksi. Na naslednji sliki je prikazan še en primer.

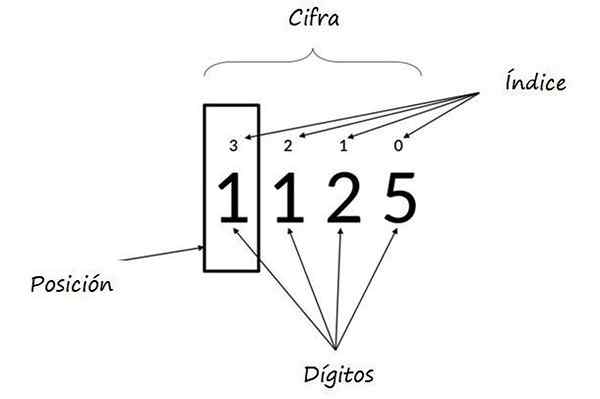V številki 1125 je relativna vrednost 5 5, 2 je 20, 1 je 100, leva 1 v škatli. Vir: Wikimedia Commons.

Številka 63

Od leve proti desni je 3 v položaju enot, zato:

Relativna vrednost 3: 3 x 1 = 3

Kar zadeva 6, je to v položaju desetin, potem pa:

Relativna vrednost 6: 6 x 10 = 60

Številka 603

Ta številka se razlikuje od prejšnje, ker čeprav je relativna vrednost 0 0, imajo druge števke različne relativne vrednosti. Začenši od desne proti levi kot vedno:

• Relativna vrednost 3: 3 x 1 = 3
• Relativna vrednost 0: 0 x 10 = 0
• Relativna vrednost 6: 6 x 100 = 600

Številka 630

V tem primeru je 0 v položaju enot:

• Relativna vrednost 0: 0 x 1 = 0
• Relativna vrednost 3: 3 x 10 = 30
• Relativna vrednost 6: 6 x 100 = 600

Rešene vaje

Vaja 1

Navedite relativno vrednost podčrtanih števil:

a) 1209

b) 2782

c) 376

d) 3045

e) 273

Rešitev

a) Število 1 v 1209 zaseda položaj tisoč ali tisoč. Zato je njegova relativna vrednost 1000.

VR (1) = 1 x 1000 = 1000

b) 2 zaseda položaj enot leta 2782, zato je njegova relativna vrednost 2.

c) Leta 376 je 7 v položaju desetin in::

VR (7) = 7 x 10 = 70.

d) Leta 3045 je 4 tudi v položaju desetin:

VR (4) = 4 x 10 = 40.

e) Do 273 je 3 na mestu enot in njihova relativna vrednost sovpada s figuro številke, to je:

Vam lahko služi: šesterokotna piramida

VR (3) = 3 x 1 = 3

Vaja 2

Napišite najnižjo število 5 števk, brez ponovitve in izpolnite naslednje pogoje:

a) da so vse številke različne

b) ima 7 na tisoč

c) 8 je v položaju enot.

Rešitev

Najmanjša številka 5 -digit z vsemi se mora začeti za 1, saj je 0, čeprav je 0 nižja, saj prva številka leve ne šteje, zato je število iskanih:

10234

Rešitev b

Millar položaj za 7 ustreza 7000, a ker želite najmanjšo možno številko, ki vsebuje 5 števk, se mora številka zagnati do 1, nato pa v preostalih položajih sledi 7 in nato 023, saj ni treba ponoviti številke.

Zato je številka:

17023

Rešitev c

Na zahtevo, da je 8 v položaju enot, mora biti do skrajne desnice. Ker je najmanj možna številka, ne da bi se katera koli od njegovih 5 števk ponovila, je iskana številka:

10238

Vaja 3

Izračunajte absolutno in relativno vrednost (vsake slike) številke 579.

Rešitev

Ima, da je 579 enakov 5 × 100+7 × 10+9 × 1 ali enakovredna, enaka 500+70+9. Zato je relativna vrednost 5 500, relativna vrednost 7 je 70, 9.

Po drugi strani je absolutna vrednost 579 enaka 579.

Vaja 4

Dajte številko 9.648.736, kakšna je relativna vrednost 9 in prve 6 (od leve proti desni)? Kakšna je absolutna vrednost dane številke?

Rešitev

S prepisovanjem na številko 9.648.736 Pridobljeno je, da je to enakovredno

9 × 1.000.000 + 6 × 100.000 + 4 × 10.000 + 8 × 1.000 + 7 × 100 + 3 × 10 + 6 × 1

Lahko pa pišete kot

9.000.000 + 600.000 + 40.000 + 8.000 + 700 + 30 + 6.

Tako da je relativna vrednost 9 9.000.000 in relativna vrednost prvih 6 je 600.000.

Po drugi strani je absolutna vrednost dane številke 9.648.736.