Matematika

Absolutna vrednost

Absolutna vrednost

Kakšna je absolutna vrednost?

On absolutna vrednost realnega števila je opredeljeno kot razdalja med to številko in 0 prave črte. Ker je razdalja, je njegova vrednost vedno pozitivna ali nič in enaka številka števila.

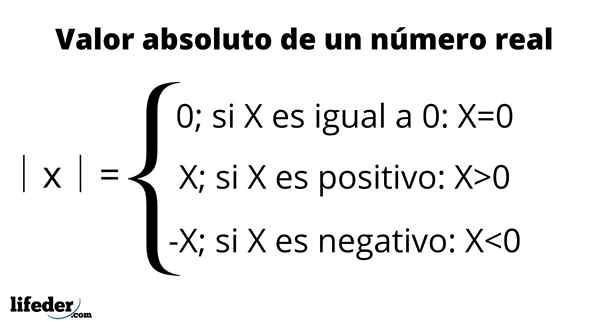
Absolutna vrednost je predstavljena z namestitvijo številke med dve navpični vrstici, simbol, ki se bere: "absolutna vrednost", Kot je povzeto v naslednji tabeli:

Na primer, absolutna vrednost -3 je zapisana kot │ -3│ in je enaka 3. To pomeni, da med -3 in 0 obstajajo tri enote, ki predstavljajo številke na resnični črti. Po drugi strani je absolutna vrednost +3 ali preprosto 3 enaka tudi 3, saj z merjenjem razdalje do 0 je tudi tri enote.

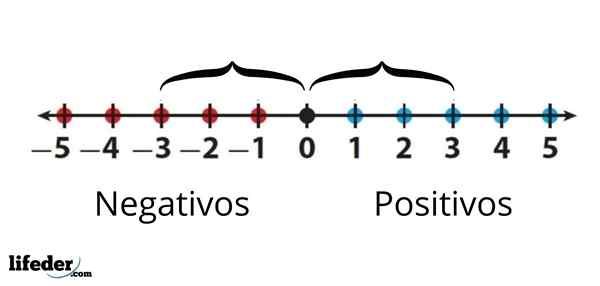Absolutna vrednost -3 je enaka absolutni vrednosti +3, saj je razdalja med bodisi na 0 enaka

Če povzamemo, je absolutna vrednost številke enaka številka številke, vendar vedno s pozitivnim znakom.

Lastnosti absolutne vrednosti

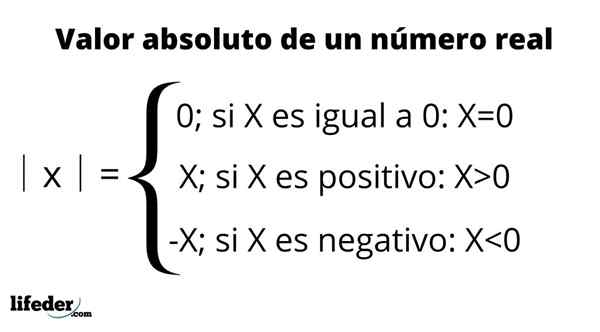Opredelitev absolutne vrednosti

Glavne lastnosti absolutne vrednosti:

  • 1) Absolutna vrednost številke je vedno pozitivna ali 0, zato:

│x│≥ 0

  • 2) Absolutna vrednost nič je tudi nič, to je │0│ = 0, zato je mogoče potrditi, da:

│x│ = 0, da y samo, če x = 0

  • 3) Za vsako število X, ki spada v nabor realnih števil, je absolutna vrednost x enaka absolutni vrednosti - x:

│x│ = │ - x│

  • 4) Če je absolutna vrednost številke x A, to pomeni, da za to številko obstajata dve možnosti: i) x = +a ali ii) x = -a.
Lahko vam služi: Mary potuje 2/4 cikla, Melissa potuje 4/8 in Anahi Potovanja 3/6

Na primer, če je absolutna vrednost številke 5, sta dve možnosti, da je številka +5 ali -5.

Operacije z absolutno vrednostjo

Naslednje lastnosti so zelo koristne za delovanje z absolutnimi vrednostmi:

  • 5) Za "x" in "y", ki sta dve resnični številki, se vedno izpolnjuje naslednja neenakost, imenovana Trikotna neenakost absolutne vrednosti:

│x│+│y│≥ │x+y│

Na primer, biti:

x = -6

y = 9

Leva stran neenakosti je:

│-6│ + │9│ = 6 + 9 = 16

In desna stran je:

│-6+9│ = │3│ = 3

Očitno je 16 večjih ali enakih 3, in to je vedno tako, ko številke x in in imajo različne znake. Če imajo enake znake, potem dobimo enakost. Oglejte si ta drugi primer z dvema različnima vrednostima:

x = -5

y = -3

│-5│+│-3│≥ │-5-3│

5+3≥│-8│

Prav zares:

8 = 8

  • 6) Produkt ustreznih absolutnih vrednosti dveh realnih številk "x" in "y" je enak absolutni vrednosti produkta števil:

│x│ ∙ │y│ = │x ∙ y│

Spet so vrednosti:

x = -6

y = 9

Tako:

│-6│ ∙ │9│ = 6 ∙ 9 = 54

Ki je enako:

│ (-6) ∙ 9│ = │-54│ = 54

  • 7) Quostient absolutne vrednosti dveh resničnih številk "x" in "y" z različnim imenovalcem 0 je absolutna vrednost količnika med temi številkami:

Dokler in ≠ 0.

Primer:

Primeri absolutne vrednosti

Preprosti primeri

Izračun absolutne vrednosti katerega koli realnega števila je zelo preprosto, na primer absolutna vrednost naslednjih številk je:

a) │-14│ = 14

b) │-(-5) │ = │5│ = 5

c) │π│ = π

Izračuni z absolutno vrednostjo realne številke

Izvedite naslednje operacije, ki vključujejo absolutno vrednost:

a) 2⋅│8│ + 5⋅│ -16│ -⋅│4│ = (2⋅8) + (5⋅16) - 4 = 16 + 80 - 4 = 92

b) │5- (8⋅3) │- 6 + │81 ÷ (-3) │ 

Vam lahko služi: polovica od 15

To je kombinirana operacija, zato ga je bolje rešiti po korakih. Prva absolutna vrednost je:

│5- (8⋅3) │ = │5-24│ = │-19│ = 19

Druga absolutna vrednost, ki se pojavi, se izračuna na naslednji način:

│81 ÷ (-3) │ = │-27│ = 27

Nato se zbirajo dobljeni rezultati in končni izračun se izvede:

│5- (8⋅3) │- 6 + │81 ÷ (-3) │ = 19- 6 + 27 = 40

Razdalja med dvema točkama na pravi črti

Absolutna vrednost se pojavlja v mnogih aplikacijah, na primer iskanje razdalje med dvema številkama, ki pripadata resnični vrstici. Če je A realna številka, se nahaja na pravi črti na mestu, katere abscisa je "A", enako se zgodi z resnično številko B.

Naj bo "A" in "B" dve številki na resnični črti, razdalja, ki jih loči, je:

dAb = │b - a│

Ki jih lahko izračunamo tudi:

dAb = │a - b│

Na primer, razdalja med A = 5 in B = 12 je:

D = │5−12│ = │12–5│ = 7

Na ta način je absolutna vrednost odštevanja med dvema resničnima številkama preprosto razdalja, ki jih loči na resnični črti.

Funkcija absolutne vrednosti

Funkcija absolutne vrednosti je aplikacija, ki gre na nabor realnih številk do ℛ+, ki ustreza vsaki realni številki njena absolutna vrednost. Definira ga:

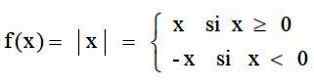
In njegov graf ima značilno V obrazec:

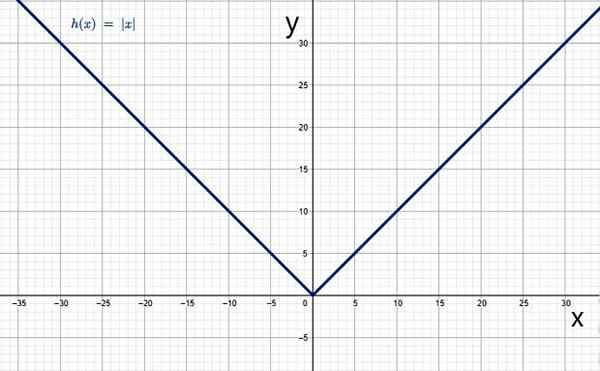Absolutna vrednost kot funkcija. Vir: f. Zapata skozi Geogebro.

Značilnosti funkcije absolutne vrednosti

-Vaša domena je nabor vseh resničnih številk.

-Je neprekinjeno.

-Celo, ker je izpolnjeno, da je f (x) = f (-x), zato je navpična os os simetrije.

-Obseg funkcije absolutne vrednosti je nabor pozitivnih resničnih, vključno z 0, saj funkcija vedno predstavlja razdaljo, in to je vedno pozitivno ali nično.

Vam lahko služi: kakšna je smernica? (Geometrija)

-Je funkcija po odsekih ali po delih.

-Zmanjša se v intervalu (-∞, 0) in raste v (0,+∞).

Argument absolutne vrednosti je lahko tudi kvadratna ali druga funkcija, na primer je mogoče opredeliti:

  • f (x) = │x2-5x+3│
  • g (x) = │sen x│

Absolutna vrednost je odgovorna za to, da postane pozitivna slika argumenta, ki imajo negativen znak.

Rešene vaje

Vaja 1

Ocenite naslednje algebrske izraze z absolutno vrednostjo:

a) │2x -5│ + │ --x + 1│ pri x = 3

b) │ (x - 5) ÷ (x+4) │ pri x = −1

Rešitev

│2⋅3−5│ + │ - 3 + 1│ = │6−5│ + │ - 2│ = │1│ + 2 = 3

Rešitev b

│ (−1−5) ÷ (−1+4) │ = │ (−6) ÷ (3) │ = │ - 2│ = 2

Vaja 2

Kakšen je niz vrednosti, ki predstavlja naslednjo neenakost?

│x│≤ 3

Rešitev

Neenakost predstavlja vse realne številke, katerih absolutna vrednost je manjša ali enaka 3, zato je niz vseh številk med -3 in +3, vključno z njimi.

V intervalnem zapisu ostaja:

[-3,3]

Vaja 3

Rešite naslednjo enačbo z absolutno vrednostjo:

│2x-1│ = 5

Rešitev 

Kot je bilo že omenjeno, je treba za reševanje enačbe z absolutno vrednostjo upoštevati obe možnosti. Mislim, da:

│f (x) │ = c

Tako:

1) f (x) = c

2) f (x) = -c

Zato ima ta enačba, katere argument je linearna, dve rešitvi:

Prva rešitev

2x - 1 = 5

2x = 6 ⇒ x1 = 3

Druga rešitev

2x - 1 = -5

2x = -4 ⇒ x2 = -2

Pri ocenjevanju x1 = 3 ali x2 = -2 V prvotni enačbi je treba pridobiti enakost, na ta način je preverjeno, da so pridobljene vrednosti rešitev predlagane enačbe. Prav zares:

│ (2⋅3) -1│ = │6-1│ = 5

In ko poskusite z drugo možnostjo, dobimo tudi enakost:

│2⋅ (-2) -1│ = │-4-1│ = 5

Reference

  1. Baldor, a. 2005. Algebra. Kulturna domovinska skupina.
  2. Larson, r. 2012. Prekalenkulacija. 8. Izdaja. Cengage učenje.
  3. Hoffman, J. Izbira vprašanj matematike. Zvezek 2.
  4. Stewart, J. 2007. Predhodno: matematika za izračun. 5. Izdaja. Cengage učenje.
  5. Zill, d. 1984. Algebra in trigonometrija. McGraw Hill.