Ovalne (geometrijska slika) značilnosti, primeri, vaje

On ovalni Simetrična je opredeljena kot ravna in zaprta krivulja, ki imata dve pravokotni simetrični osi - eno večjo in eno manjšo - in je sestavljen iz dveh krožnih lokov, enaka dva do dva do dva do dva do dva do dva do dva do dva do dva do dva do dva do dva do dva.

Na ta način lahko narišete s pomočjo kompasa in nekaj referenčnih točk na eni od osi simetrije. Vsekakor obstaja več načinov, kako ga narisati, kot bomo videli kasneje.

Slika 1. Pogled na kolosej Rima, primer ovalne oblike v arhitekturi. Vir: Pixabay.

To je zelo znana krivulja, saj je prepoznana kot kontura elipse, kar je poseben primer ovalne. Toda oval ni elipsa, čeprav se včasih zdi veliko, saj se njene lastnosti in sledi razlikujejo. Na primer elipsa ni zgrajena s kompasom.

[TOC]

Značilnosti

Oval ima zelo raznolike aplikacije: arhitektura, industrija, grafično oblikovanje, urejanje in nakit so le nekatera področja, kjer izstopa njegova uporaba.

Najbolj izjemne značilnosti te pomembne krivulje so naslednje:

-Spada v skupino tehničnih krivulj: sledi je oblikovanju obodov s pomočjo kompasa.

-Vse njegove točke so na isti ravnini.

-Manjka krivulje ali kravate.

-Njegova postavitev je neprekinjena.

-Ovalna krivulja mora biti mehka in konveksna.

-Ko privadite tangentno črto na oval, je vse na isti strani črte.

-Oval podpira dve tangenti, vzporedni z večino.

Primeri

Obstaja več načinov za izgradnjo ovalov, ki zahtevajo uporabo pravil, moštev in kompasa. Potem bomo omenili nekaj najbolj uporabljenih.

Vam lahko služi: neenakost trikotnika: demonstracija, primeri, rešene vaje

Gradnja ovala s koncentričnimi okoliščinami

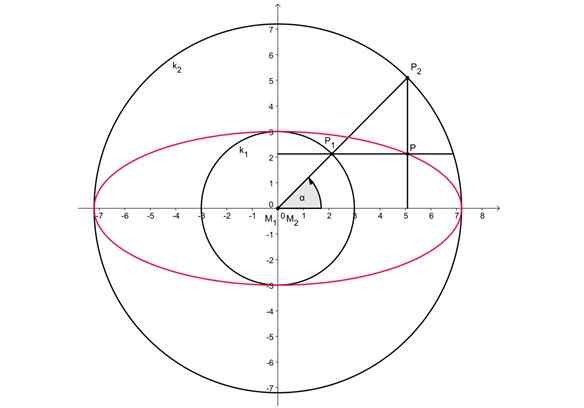
Slika 2. Način, da potegnete oval skozi dve koncentrični okolici. Vir: Wikimedia Commons. Kmhkmh [cc do 3.0 (https: // creativeCommons.Org/licence/by/3.0)]

Slika 2 zgoraj prikazuje dva koncentrična oboda s sredino na izvoru. Glavna ovalna os meri enako kot premer zunanjega oboda, medtem ko manjša os ustreza premeru notranjega oboda.

-Na zunanji obod se privleče poljubni polmer, ki v P -točkah zmanjša oba oboda₁ In p₂.

-Potem je točka P projicirana₂ Na vodoravni osi.

-Na podoben način je točka P projicirana₁ na navpični osi.

-Presečišče obeh projekcij je točka P in pripada ovalu.

-Vse točke v tem razdelku ovala je mogoče narisati na ta način.

-Preostanek ovala je narisan s analognim postopkom, izveden v vsakem kvadrantu.

Vaje

Potem bodo pregledani drugi načini za izgradnjo ovalov, glede na določen začetni ukrep, ki bo določil njegovo velikost.

- Vaja 1

Narišite s pravilom in kompasom ovalno, ki je znana njegova glavna osi, katere dolžina je 9 cm.

Rešitev

Na sliki 3, ki je prikazana spodaj, se rezultat oval pojavi v rdeči barvi. Posebno pozornost je treba nameniti pikčastim črtam, ki so pomožne konstrukcije, potrebne za risanje ovala, katere glavna os je določena. Nakazali bomo vse potrebne korake za dosego končne risbe.

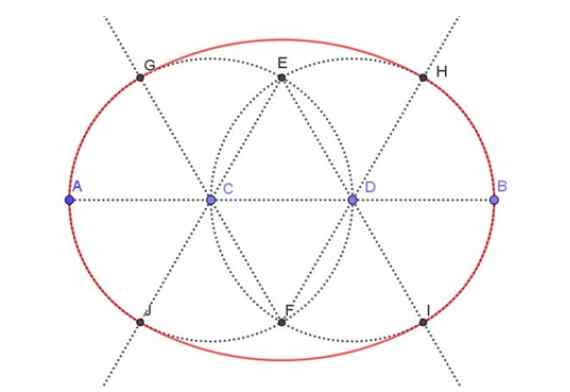Slika 3. Gradnja ovala glede na svojo glavno osi. Vir: f. Zapata.

Korak 1

Narišite 9 cm AB segment s pravilom.

Vam lahko služi: Bayesovi teorem

2. korak

Trisektiranje AB segmenta, to je, da ga delimo na tri segmente enake dolžine. Ker originalni segment AB meri 9 cm, segmenti AC, CD in DB morajo izmeriti po 3 cm.

Korak 3

S kompasom, izdelava C in Ca, otvoritve pritegne pomožni obod. Podobno je s kompasom narisan pomožni obod središča D in radia DB.

4. korak

Označena so križišča obeh pomožnih okoliščin, vgrajeni v prejšnjem koraku. To imenujemo točke E in F.

5. korak

S pravilom naslednje polkrenije.

6. korak

Pol -utrip prejšnjega koraka se je zmanjšala na dve pomožni okolici v točkah g, h, i, j.

7. korak

S kompasom je izdelan v središče v F in z odpiranjem (ali radia) FG je lok narisan Gh. Podobno je izdelava središča na E in z radio EI lok Ij.

Korak 8

Zveza lokov Gj, Ji, Ih in Hg Tvorijo oval, katerega glavna os meri 9 cm.

Korak 9

Pomožne točke in udarce so izbrisane (skriti).

- Vaja 2

Narišite s pravilom in kompasom ovalno, katere manjša osi je znana in njen ukrep je 6 cm.

Rešitev

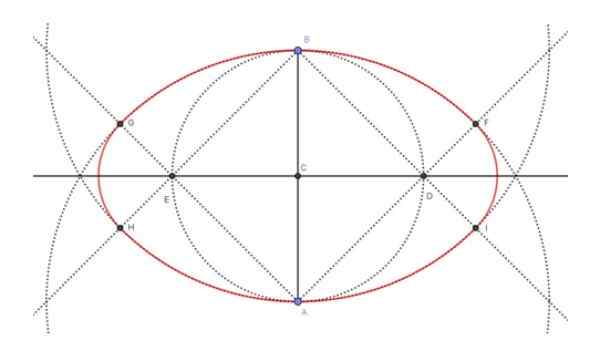Slika 4. Gradnja ovala glede na svojo manjšo osi. Vir: f. Zapata.

Slika zgoraj (slika 4) prikazuje končni rezultat konstrukcije ovalne (v rdeči barvi), pa tudi vmesne konstrukcije, potrebne za dosego nje. Sledili so koraki, ki so sledili za izgradnjo manjše osi ovalne 6 cm: naslednje:

Korak 1

6 cm dolg segment AB je narisan s pravilom.

Vam lahko služi: teorija nastavitve: značilnosti, elementi, primeri, vaje

2. korak

S kompasom in pravilom je Mediatrix pritegnjen v segment AB.

Korak 3

Presečišče Mediatrixa s segmentom AB ima za posledico sredino C segmenta AB.

4. korak

S kompasom se nariše obod centra c in radia CA.

5. korak

Obseg, narisan v prejšnjem koraku, prestreže mediatrix AB v točkah E in D.

6. korak

Selični [AD), [AE), [BD) in [BE) so narisani.

7. korak

S kompasom so narisani Center A in Radio AB ter Centro B ter Radio BA Radio B ter Radio BA.

Korak 8

Križišča obrob, narisana v koraku 7, s pol -utripom, vgrajenim v korak 6, določajo štiri točke, in sicer: F, G, H, i.

Korak 9

Z sredino mesta v D in Radio di lok, če je narisano. Na enak način je z E in radiom EG narisan GH lok.

Korak 10

Zveza oboda lokov FG, GH, HI in če določite iskani ovalni.

Reference

1. Plastična ed. Tehnične krivulje: ovalne, ovoidne in spirale. Okrevano od: RIAT.WordPress.com.
2. Mathematische Basteleien. Jajčne krivulje in ovali. Pridobljeno od: Mathematische-Basteleien.
3. Univerza v Valenciji. Stožčaste in ravne tehnične krivulje. Okreval od: OCW.UV.je.
4. Wikipedija. Ovalni. Okrevano od: je.Wikipedija.org.
5. Wikipedija. Ovalni. Pridobljeno iz: v.Wikipedija.org.