Premer simboli in formule, kako ga odpeljati, obod

On premer Ravna črta gre skozi sredino zaprte ravne krivulje ali figuro v dveh ali treh dimenzijah, ki se pridruži tudi njenim nasprotnim točkam. Običajno je krog (ravna krivulja), krog (ploščata figura), krogla ali ravnega krožnega valja (trijedimenzionalni predmeti).

Čeprav se obod in krog običajno jemljeta kot sinonimi, obstaja razlika med obema izrazoma. Obseg je zaprta krivulja, ki se zajema v krog, ki izpolnjuje pogoj, da je razdalja med katero koli od njegovih točk in sredino enaka. Ta razdalja ni nič drugega kot polmer oboda. Namesto tega je krog ravna figura, omejena z obodom.

Slika 1. Premer kolesnih koles je pomembna lastnost pri njegovem dizajnu. Vir: Pixabay.

V primeru oboda, kroga in krogle je premer ravni segment, ki vsebuje vsaj tri točke: sredino plus dve točki roba oboda ali kroga ali površino krogle.

In kar se.

Premer oboda in kroga, ki ga simbolizira Ø ali preprosto črka "D" ali "D", je povezan z njegovim obodom, konturo ali dolžino, ki je označena s črko L:

L = π.D = π. tudi

Kadar koli imate obod, je količnik med njegovo dolžino in premerom iracionalno število π = 3.14159 ..., na ta način:

π = l/d

[TOC]

Kako dobiti premer?

Ko je na voljo risba oboda ali kroga, ali neposredno krožni predmet, na primer valuta ali obroč, je zelo enostavno vzeti premer s pravilom. Preprosto se morate prepričati, da ima rob pravila hkrati dve točki oboda in središče istega.

Vam lahko služi: algebrski

Kaliber, vernir ali kraljevo stopalo je zelo primeren za merjenje zunanjih in notranjih premerov v kovancih, obročkih, obročih, oreščkih, cevi in ​​še več.

Slika 2. Vernier digitalno merjenje premera kovanca. Vir: Pixabay.

Če namesto predmeta ali njegove risbe imate podatke, kot je radio R, Nato pomnožite po 2. In če je znan dolžina ali obod oboda, lahko premer poznamo tudi z odmikom:

D = 2.R
D = l / π

Drug način, da dobite premer, je poznavanje območja kroga, sferične površine, preseka valja, ukrivljenega območja te ali količine krogle ali valja. Vse je odvisno od tega, katera geometrijska figura je. Na primer, premer je vključen v naslednja območja in količine:

-Območje kroga: π.(D/2)²
-Sferična površina: 4π.(D/2)²
-Prostornina krogle: (4/3) π.(D/2)³
-Volumen ravnega krožnega valja: π.(D/2)².H (H je višina valja)

Številke stalnega širokega

Krog je ravna figura konstantne široke, saj kjer koli je videti, širina je premer D. Vendar obstajajo tudi druge morda manj znane številke, katerih širina je tudi stalna.

Najprej poglejmo, kaj se razume s širino slike: razdalja med dvema vzporednima črtama -podpira reme -, ki sta posledično pravokotni na dano smer in to zapirajo figuro, kot je prikazano na levi sliki:

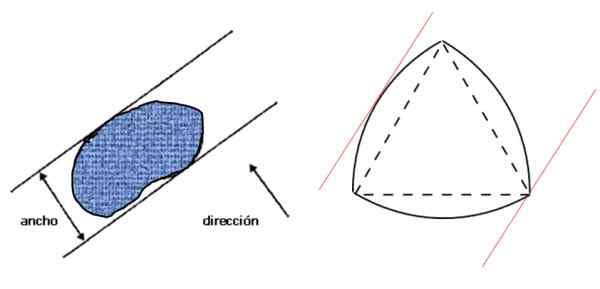Slika 3. Širina katere koli ravne figure (levo) in Reuleaux trikotnik, konstantna široka figura (desno). Vir: f. Zapata.

Potem je desno trikotnik Reuleaux, ki je stalna široka figura in ki izpolnjuje pogoj, določen na levi sliki. Če je širina figure d, je njegov obod podan z Barbierjevim teoremom:

Vam lahko služi: Približno merjenje amorfnih številk: Primer in vadba

L = π.D

Kanalizacije mesta San Francisco v Kaliforniji so oblikovane kot Reuleauxov trikotnik, ki ga je poimenoval nemški inženir Franz Reuleaux (1829 - 1905). Na ta način tapas ne more padati v luknjo in porabiti manj materiala za njihovo izdelavo, ker je njihovo območje manj kot v krogu:

A = (1- √3).πd² = 0.705.D²

Medtem ko za krog:

A = π.(D/2)² = (π/4) d²= 0.785.D²

Toda ta trikotnik ni edina stalna široka figura. Klice je mogoče zgraditi Poligoni Reuleaux z drugimi poligoni, ki imajo nenavadno številko.

Premer oboda

Na naslednji sliki so elementi oboda, opredeljeni na naslednji način:

Vrv: linijski segment, ki se pridruži dve točki oboda. Na sliki je vrv, ki se pridruži točkam C in D, vendar je mogoče izslediti neskončne strune, ki so edinstveni poljubni nekaj točk oboda.

Premer: Vrv je, ki gre skozi središče in se pridruži dve točki oboda s središčem oz. To je najdaljša vrv oboda, zato se imenuje "glavna vrv".

Radio: linijski segment, ki se pridruži centru s katero koli točko oboda. Njegova vrednost, tako kot premer, je konstantna.

Obod: To je niz vseh točk enakovredna oz.

Priklon: Opredeljen je kot obodni segment, ki ga imata dva radija (ni narisana na sliki).

Slika 4. Deli oboda, vključno s premerom, ki poteka skozi sredino. Vir: Wikimedia Commons.

- Primer 1

Prikazan pravokotnik je visok 10 centimetrov, ki pri navijanju tvori ravni krožni valj, katerega premer je 5 centimetrov. Odgovorite na naslednja vprašanja:

Lahko vam služi: medsebojno izključujoči dogodki: lastnosti in primeri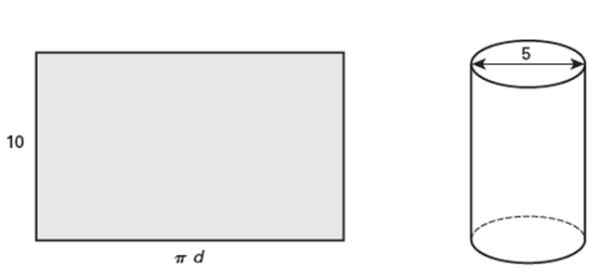Slika 5. Valjani pravokotnik postane ravno krožni valj. Vir: Jiménez, R. Matematika II. Geometrija in trigonometrija. 2. mesto. Izdaja. Pearson.

a) Kakšna je kontura cevi?
b) Poiščite območje pravokotnika
c) Izračunajte območje prereza valja.

Rešitev

Kontura cevi je l = π.D = 5π plg = 15.71 plg.

Rešitev b

Območje pravokotnika je Osnovna višina x, Ker je baza L že izračunana in višina je 10 plg po izjavi:

A = 15.71 plg x 10 plg = 157.1 plg².

Rešitev c

Končno se zahtevano območje izračuna na naslednji način:

A = π.(D/2)² = (π/4) d² = (π/4) x (5 plg)²= 19.63 plg².

- Primer 2

Izračunajte zasenčeno območje slike 5A. Trg ima stran l.

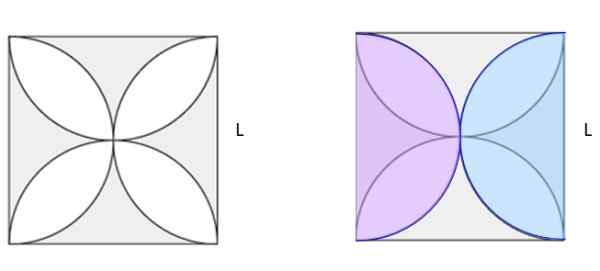Slika 6. Poiščite zasenčeno območje na levi sliki. Jiménez, r. Matematika II. Geometrija in trigonometrija. 2. mesto. Izdaja. Pearson.

Rešitev

Na sliki 5B sta narisana dva enaka polkroga velikosti v roza in modri barvi, narisana na prvotni sliki. Med njimi naredijo popoln krog. Če se izračuna kvadrat kvadrata in odšteje območje kroga, naredi senčno območje slike 5b. In videti dobro, izkaže se, da je polovica senčenega območja v 5A.

-Območje kvadrata: l²
-Premer polkroga: l
-Območje kroga: π.(L/2)²= (π/4) l²
-Razlika območij = polovica zasenčenega območja =

L² - (π/4) l² = [(4 - π)/4] l²= 0.2146 l²

-Zasenčeno območje = 2 x 0.2146 l²= 0.4292L2

Koliko premerov ima obod?

Neskončne premere je mogoče narisati v krogu in vsak od njih meri enako.

Reference

1. Antonio. Reuleaux trikotniki in druge krivulje s konstantno širino. Okrevano od: diseminatorjev.com.
2. Baldor, a. 2002. Ravna in vesoljska in trigonometrijska geometrija. Kulturna domovinska skupina.
3. Jiménez, r. Matematika II. Geometrija in trigonometrija. 2. mesto. Izdaja. Pearson.
4. Wikipedija. Reuleaux trikotnik. Okrevano od: je.Wikipedija.org.
5. Wolfram Mathworld. Premer. Okreval od: Mathworld.Wolfram.com.