Pojasnjujemo, kaj in kakšni so disperzijski ukrepi, in dajemo več primerov

Kaj so disperzijski ukrepi?

The Ukrepi disperzije ali variacije v statistiki merijo, koliko porazdelitve podatkov iz vrednosti osrednjega ukrepa se premika, kot je povprečje ali aritmetično povprečje. Njegova vrednost je vedno pozitivna in se običajno razlikuje od 0, razen v primeru enakih podatkov.

Če disperzijski ukrep daje majhno vrednost, to pomeni, da so podatki nameščeni zelo blizu povprečju, če pa so veliki, to pomeni, da so podatki bolj razpršeni.

Disperzijski ukrepi so s statističnega vidika zelo pomembni, ne le kot aritmetični kazalniki sprememb podatkov, ampak kot neprecenljiva pomoč, kadar želite izboljšati kakovost, tako pri proizvodnji izdelkov kot pri zagotavljanju storitev.

Primer tega so uvrstitve pozornosti v bankah. Povprečni čas zakasnitve strank, ko naredijo edinstveno vrsto in se nato razdelijo v blagajni.

Vendar je disperzija nižja v posamezni vrstici, kar pomeni, da je čas posamezne pozornosti zelo podoben vsaki stranki. Kupci so izjavili, da se na ta način počutijo bolj udobno, tudi če je povprečni čas nege v obeh načinih enak.

Glavni disperzijski ukrepi

Glavni so: Rank, odstopanje, standardni odklon in koeficient variacije.

Domet

Ranka R nabora podatkov je opredeljena do razlike med največjo vrednostjo x_Max in minimalna vrednost x_min celote:

Rang = r = največja vrednost - minimalna vrednost = x_Max - x_min

Vam lahko služi: za kaj so številke? 8 glavnih uporabe

Območje je hitro izračunati, vendar je zelo občutljiv na skrajne vrednosti in ima pomanjkljivost, da ne upoštevamo vmesnih vrednosti. Zato se uporablja le za začetno, precej približno predstavo o disperziji podatkov.

Primer ranga

To je seznam števila orkanov v Atlantiku v zadnjih 14 letih:

8; 9; 7; 8; petnajst; 9; 6; 5; 8; 4; 12; 7; 8; 2

Podatki o največji vrednosti so 15, najmanjša vrednost pa 2, torej:

R = največja vrednost - minimalna vrednost = x_Max - x_min = 15 - 2 = 13 orkanov

Odstopanje

Ta ukrep se uporablja za primerjavo vsakega od podatkov s povprečjem niza in se izračuna tako.

Biti:

-Povprečje: μ

-Vsaka vrednost, ki pripada naboru podatkov: x_Yo

-Skupno število opazovanj: n

Označevanje variance populacije, kot je σ², Izraz za izračun je:

In ko jemljemo vzorec populacije, je raje izračunati varianco na ta način:

Kjer je bila vzorčna varianca označena s S, in povprečje kot x s palico. Razlog za delitev med N-1, namesto N, je, da varianta vzorca ne podcenjuje populacije, kaj se vedno zgodi, ko se deli med n.

Po drugi strani je ideja, da se vsaka razlika med podatki in povprečjem prepreči, da bi jih dodajali 0, saj bodo nekatere razlike pozitivne in druge negativne, kar ponavadi prekliče vsoto. Namesto tega so kvadratki vedno pozitivni.

Lahko vam služi: verjetnost frekvence: koncept, kako se izračuna in primeri

Zato je odstopanje vedno pozitivno, tudi če je razlika med x_Yo In povprečje je negativno, njegova glavna prednost variance pa je, da upošteva vsake podatke nabora.

Vendar ima neprijetnosti, da njegove enote niso enake tistim v podatkih, na primer, če so ti sestavljeni v časih, merjene v minutah, bo odstopanje nabora v nekaj minutah podane na kvadrat.

Primer variance

Izračun variance zahteva iskanje povprečja. Če upoštevamo podatke o orkanu, se povprečje izračuna z:

(8 + 9 + 7+ 8 + 15 + 9 + 6 + 5+ 8 + 4 + 12 + 7 + 8+ 2)/14 = 7.7 orkanov.Zato je varianta:

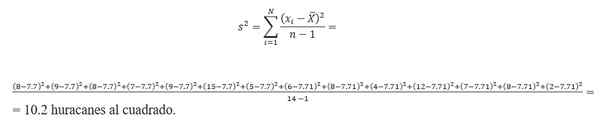
Standardni odklon

Za odpravo problema pomanjkanja skladnosti med enotami je določen standardni odklon σ, Kot kvadratni koren variance:

In analogno, v primeru vzorca:

Obstaja empirično pravilo za oceno vrednosti standardnega odklona vzorčnega nabora podatkov na podlagi območja. V skladu s tem pravilom je standardni odklon približno četrtina R:

S ≈ r/4

Prednost ima hitro oceno standardnega odstopanja, saj so operacije veliko enostavnejše.

Standardni odklon je z veliko najpogosteje uporabljenim disperzijskim ukrepom, zato je vredno poudariti njegove glavne značilnosti:

• Standardni odklon kaže, koliko se medijski podatki premaknejo
• Vedno je pozitiven, vendar je lahko 0, če so vsi podatki enaki
• Večja kot je vrednost standardnega odklona, ​​bolj razpršeni so podatki
• Enote standardnega odklona so enake tistim pri preučevanju spremenljivke
• Njegova vrednost se hitro spremeni, ko ima eden od podatkov (ali več) zelo drugačno vrednost od ostalih
• Vrednosti standardnih odstopanj so pristranske, to je, da povprečje standardnega odklona niso razporejene okoli povprečja.

Vam lahko služi: akutantni trikotnik

Primer standardnega odklona

Nadaljevanje s primerom orkanov je standardni odklon:

Ali pa je, če je najraje uporaba pristopa standardnega odklona skozi območje, dobimo dokaj zaprta vrednost:

S = 13/4 = 3.25

Koeficient variacije

Koeficient variacije je v nekaterih besedilih označen s CV ali R začetnicami, tako za populacijo kot za vzorec, kot odstotek navaja standardno in povprečno odstopanje:

O No:

Enačbe veljajo, dokler se povprečje razlikuje od 0.

Praviloma je koeficient variacije zaokrožen na eno decimalno in se uporablja za primerjavo podatkov iz dveh različnih populacij.

Primer koeficienta variacije

Čakalne dobe v nekaj sekundah za stranke banke so zabeležene v dveh situacijah: ko naredijo edinstveno vrsto in ko naredijo individualne vrste pred uradom za vozovnice za pozornost. Rezultati so naslednji:

Oba nabora podatkov lahko primerjamo s svojim koeficientom variacije:

Enotna vrstica

• Povprečno = 429 sekund
• Odstopanje = 28.6 sekund
• Cv = (28.6/429) x 100 = 6.7 %

Posamezne vrste

• Povprečno = 429 sekund
• Odstopanje = 109.3 sekunde
• Cv = (109.3/429) x 100 = 25.5 %

Ker je ta zadnja vrednost večja, to kaže, da je več spremenljivosti v času storitve za stranke, ko posameznike naredijo, kot ko naredijo edinstveno vrstico, čeprav je povprečni čas v vsakem primeru enak.