OBTUSE TRIKANJE

Pojasnjujemo, kaj je pripaden trikotnik, njegovi elementi, značilnosti, vrste, primeri in rešena vaja

Za obtuse trikotnik je značilen, da ima notranji kot, večji od 90 °

Kaj je obljuden trikotnik?

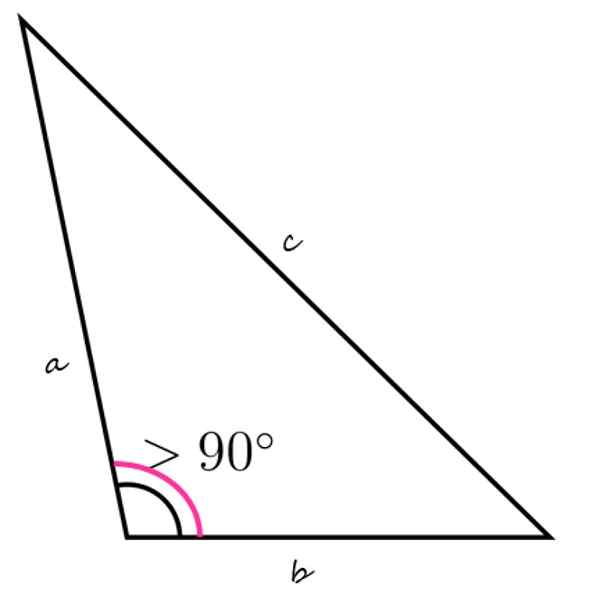
A OBTUSE TRIKANJE To je ravna figura, zaprta in s tremi stranicami, ki vsebuje tudi notranjega notranjega kota, torej večjega od 90 ° in manj kot 180 °.

Vsak trikotnik vsebuje 3 notranje kote, in če je eden od njih obljubljen, sta druga dva akutna, ker je vsota notranjega kota katerega koli trikotnika vedno enaka 180 °.

Zgornja slika prikazuje primer obtusenega trikotnika, s spodnjim levim notranjim kotom, večjim od 90 °. Preostali notranji koti morajo dodati manj kot 90 °, le na ta način je res, da je vsota treh enaka 180 °.

Poleg obtujenih trikotnikov obstajajo akutanguzni trikotniki, če so vsi njegovi notranji koti akutni, in pravokotni trikotniki, ko eden od notranjih kotov meri natanko 90 °.

Elementi obrobnih trikotnikov

Trikotniki obtusángulos imajo skupne elemente vsem trikotnikom: so 3 -stranske plošče, s 3 notranjimi koti in 3 točki. Poleg tega imajo pomembne segmente, imenovane Cevijci, kot so višina, mediana in mediatrix ter točke, kjer se sekajo cevijci.

Vsak od teh elementov je na kratko opredeljen na naslednji način:

-Strani, so segmenti, ki sestavljajo figuro.

-Točke, Točke križišča vsakih par sosednjih strani.

-Notranji koti, Sta med dvema sosednjima stranicama, na notranji strani slike, ki sovpadata točko kota s trikotnikom.

-Zunanji koti, So med eno stranjo in razširitvijo sosednje strani, zunaj slike, tako da je to vrhovi pogost, tako trikotnik kot kota. Vsota ukrepa med notranjim kotom in njegovim zunanjim sosednjim kotom je 180 °, tako da so dopolnilni koti.

Lahko vam služi: Tukey Test: Kaj je v primeru, da je v primeru rešena vaja

-Višina, Ukrep pravokotnega segmenta se pridruži točki z nasprotno stranjo ali s podaljšanjem tega.

-Mediana, linija, ki je usmerjena od točke do središča nasprotne strani.

-Mediatrix, segment, pravokoten na stran, in to poteka tik skozi njegovo središče.

-Bisektor, To je segment, ki se deli na pol notranjega kota trikotnika.

-Orocentro, presečišče treh višin.

-Barycenter, Imenuje se tudi Centroid, to je točka, ko se trije mediani sekajo.

-OCCENTRO, Tu so tri mediatrices razrezane.

-Spodbuda, Točka sotočja bisektorjev.

Ko so ti koncepti pregledani, so spodaj opisane nekatere najpomembnejše značilnosti obrobnih trikotnikov.

Značilnosti

1.- Vsota treh notranjih kotov objemnega trikotnika je 180 °, zato je lahko le eden od njegovih notranjih kotov večji od 90 °, medtem ko je vsota preostalih dveh manjša od 90 °.

2.- Najdaljša stran obtusenega trikotnika nasprotuje zbolenemu kotu.

3.- V zastrašujočem trikotniku višine iz tokov, ki naredijo akutni kot, prečkajo podaljške nasprotnih strani.

4.- Ortocenter zajetnega trikotnika je zunaj slike.

5.- Oborišča objemnega trikotnika prav tako izpade iz trikotnika (to se ne zgodi s trikotnikom Acutangle).

6.- Možno je le registrirati kvadrat v obtusenem trikotniku, ki podpira eno od strani trga na najdaljši strani trikotnika. Dva kvadrata je mogoče narisati, ki podpirata stran na najkrajših straneh trikotnika, tako da vrhova ne bo registrirana (ki se ne dotika strani trikotnika).

Vam lahko služi: tidecágono

7.- Biti obljubni trikotnik stranskih strani (a, b, c), ki je c najdaljša stran. Naslednja neenakost je veljavna:

do²+b² < c²

8.- To sta dva obljubljena trikotnika, katerih strani sta (A, B, C) in (U, V, W). Najdaljše strani vsakega sta C in W, zato je izpolnjena naslednja neenakost:

A ∙ u + b ∙ V < c∙w

Vrste oviranja trikotnikov

Obražasti trikotniki so lahko dve vrsti, glede na dolžino njihovih strani:

• Izosceles
• Scalene

Na kratko so opisani spodaj:

Trikotnik izosceles

To je ena, ki ima dve enaki strani in drugačen, to je, da so njegove strani (a, a, c).

Ko je trikotnik izosceles obljubljen, so mere "A" krajše in "C" stran je najdaljša. Obtujen kot se oblikuje med istimi stranicami, medtem ko sta oba akutna kota enaka in se tvorita med stranicama "A" in stransko "C".

In kot je navedeno v prejšnjem odseku, stranski "C", ker je najdaljši, nasprotuje pripadniškemu kotu.

Trikotnik Scalene

Tri strani trikotnika skale imajo drugačno mero: (a, b, c).

Primeri

Primer 1

Trikotnik, prikazan na naslednji sliki. Obtusen kot je γ = 114.5. in preverjeno je, da je vsota treh notranjih kotov 180 °:

114.5. + 36.8 ° + 28.6. ≈ 180 °

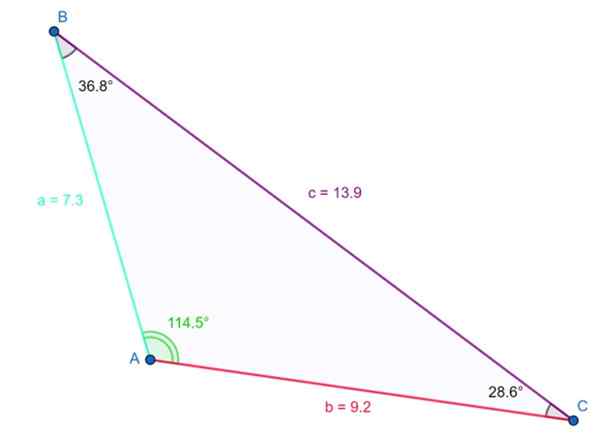Primer obtusenega trikotnika. Vir: f. Zapata

Najdaljši stranski ukrepi 13.9 enot in nasprotuje pripadniškemu kotu. Izpolnjena je tudi prej omenjena neenakost:

do²+b² < c²

Vam lahko služi: odnosi s sorazmernostjo: koncept, primeri in vaje

DA A = 7.3 in b = 9.2, potem:

7.3² + 9.2² < 13.9²

137.93 < 193.2

Primer 2

V trikotniku Calabi je možno postaviti največji možni kvadrat na tri različne načine znotraj trikotnika, kot je prikazano na naslednji sliki.

Kalabijev trikotnik je izoscele in obljuden. Obitni kot je približno 101.736 ° in akutni koti na bazi merijo oba 39.13., tudi približno.

Vaja rešena

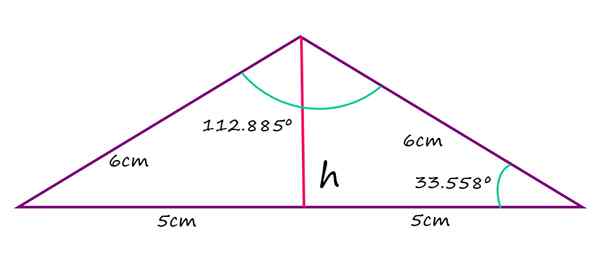
Enake strani trikotnika izosceles iz območij merijo 6 cm, medtem ko najdaljša stran meri 10 cm. Izračunajte vrednost objemnega kota, vrednosti preostalih kotov Agudos in višine od omenjene točke do baze.

Rešitev

Teorem za kosinus lahko uporabite za iskanje kosinusa obturnega kota. Nato se s pomočjo kalkulatorja določi zadevni kot, označen kot γ.

Cosenov teorem navaja, da:

c² = a² +b² - 2ab ∙ cos γ

Kjer je γ kot med stranicami A in B. Ker je trikotnik izosceles, sta strani A in B enaka:

c² = 2a² - 2. mesto²∙ cos γ

Čiščenje cos γ:

 Obitni kot je -0 kosinus.38889, kar je približno 112.885 °. Vrednost α, akutni kot, ki ga tvorijo 6 cm strani z 10 cm, je:

2α + 112.885 ° = 180 °

α = (180 - 112.885)/2 = 33.558 °

Isosceles obtuse trikotnik. Vir: f. Zapata

Kar zadeva višino trikotnika, merjeno iz osnove, dobimo z opazovanjem, da ta višina trikotnik deli na dva enaka pravokotnika, s hipotenuzo pa je enaka 6 cm in podstavek 5 cm. V takem primeru se teorem pitagore uporablja za neposredno iskanje vrednosti H: