Fourierjeve lastnosti transformacije, aplikacije, primeri

The Fourier transformacija To je metoda analitične ustreznosti, usmerjene v integrirane funkcije, ki spada v družino tcelovito ransformirano. Sestavljen je iz ponovnega opredelitve funkcij F (t) v smislu Cos (t) in sena (t).

Trigonometrične identitete teh funkcij skupaj z njihovimi značilnostmi izpeljave in antiderivacije služijo za opredelitev Fourierjeve transformacije z naslednjo kompleksno funkcijo:

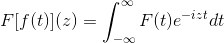
Kar je izpolnjeno, medtem ko je izraz smiseln, torej ko je nepravilni integral konvergenten. Algebraicy je rečeno, da je Fourierjeva preobrazba linearni homeomorfizem.

Vsaka funkcija, ki jo je mogoče opraviti s Fourierovo preobrazbo.

[TOC]

Lastnosti

Vir: Pexels

Fourier Transform ustreza naslednjim lastnostim:

Obstoj

Za preverjanje obstoja Fourierjeve transformacije v funkcijo f (t), določeno v Royals R, Naslednji 2 aksioma morata biti izpolnjena:

1. f (t) je neprekinjeno za vse R
2. f (t) je integriran v R

Fourierjeva transformacija Linearnost

Naj bo m (t) in n (t) dve dve funkciji z definiranim Fourierjevim preoblikovanim, s konstantami A in B.

F [a m (t) + b n (t)] (z) = a F [M (t)] (z) + b F [N (t)] (z)

Ki se opira tudi na linearnost istoimenskega integrala.

Fourier se je spremenil iz derivata

Imate funkcijo F  ki je neprekinjeno in integrirano v vseh reaisih, kjer:

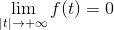
In derivat F (f ') Je neprekinjen in definiran na koščke v vsem R

Fourierovo transformacijo derivata je opredeljen z integracijo po delih, z naslednjim izrazom:

F [f '(t)] (z) = IzzF [f (t)] (z)

V izpeljavah višjega reda se bo uporabljal na homologni način, kjer morate za vse n 1:

F [f ⁿ'(t)] (z) = (iz)ⁿF [f (t)] (z)

Diferenciacija Fourierjeve transformacije

Imate funkcijo F  ki je neprekinjeno in integrirano v vseh reaisih, kjer:

I (d/dz)F [f (t)] (z) = F  [T .  f (t)] (z)

Fourier se je spremenil iz prevoda

Za vse θ ki pripada kompletu in T ki spada v set s ', morate:

F [ τ_do θ] =  in^-Iay F [ θ]                                 F [ τ_doT ] =  in^-Iax  F [ T]   

Z  τ_do  ki deluje kot prevajalski operater na vektorju.

Prevod Fourierjeve transformacije

Za vse θ ki pripada kompletu in T ki spada v set s ', morate:

τ_do F [θ] =  F [in^-Iax.θ]                                τ_do F [t ] =  F [in^-Iay . T]

Vam lahko služi: Hypercubo: definicija, dimenzije, koordinate, razgrnjene

Za vse do ki pripada R

Fourierjeva preobrazba skupine lestvice

Za vse θ ki pripada kompletu. T ki spada v komplet s '

λ pripadnost R - 0  Moraš:

F [θ (λx)] = (1 / | λ |) F [θ] (in/λ)                 

F [T (λx)] = (1 / | λ |) F [T] (in/λ)

Ja F Gre za neprekinjeno in čisto integrirano funkcijo, kjer je A> 0. Tako:

F [f (at)] (z) =   (1/a) F [f (t)] (z/a) 

Da bi pokazali ta rezultat, lahko nadaljujemo s spremembo spremenljivke.

Ko t → + potem s = at → + ∞

Ko t → - potem je s = at → - ∞

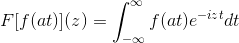
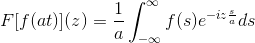
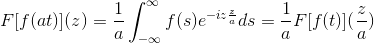
Simetrija

Preučiti simetrijo Fourierove transformacije.

Imate θ in Δ, ki pripadata S. Od tam je mogoče sklepati:

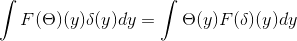
Pridobivanje

1 / (2π)^d  F [θ ], F [δ] Parseval identiteta

1 / (2π)^D/2  || F [θ ] ||_L²_R^d     Formula Plancherel

Fourier se je iz izdelka spremenil v zmedovanje

Preganjanje podobnih ciljev, ki se v Laplace Transform nanašajo na izdelek med njegovimi Fourierovimi transformacijami.

Ima F in G As 2 Functions Limited, definiran in popolnoma integriran:

F (f *g) = f (f) . F (g)

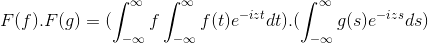
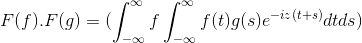
Potem pri spremembi spremenljivke

t + s = x; Dvojni integralni dvojni integral se nadaljuje

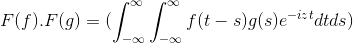
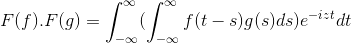
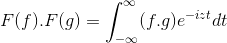
F (f) . F (g) = f (f . G)

Kontinuiteta in padec v neskončnost

Za vse θ, ki pripada R, f [ θ] Upošteva merila neprekinjene funkcije v R^d.

Tudi F [ θ] (y) → 0 v c si | y | → ∞

Zgodovina

Ta matematični koncept je predstavil Joseph B. Fourier leta 1811, medtem ko je razvijal pogodbo o Toplota. Hitro so ga sprejele različne veje znanosti in inženiringa.

Ustanovljeno je bilo kot glavno delovno orodje pri preučevanju enačb z delnimi derivati, v primerjavi celo z delovnim odnosom med Laplace transformirane in navadne diferencialne enačbe.

Za kaj je Fourierjeva preobrazba?

Služi predvsem za pomembne enačbe, hkrati pa preoblikovanje izrazov, ki izhajajo v močne elemente, ki označujejo diferencialne izraze v obliki integriranih polinomov.

Pri optimizaciji, modulaciji in modeliranju rezultatov deluje kot standardiziran izraz, ki je pogost vir za inženiring po več generacijah.

Fourierjeva serija

So opredeljene serije v smislu Cosen in dojk; Služijo za lažje delo s splošnimi periodičnimi funkcijami. Ko se uporabljajo, so del tehnik ločljivosti delnih in običajnih diferencialnih enačb.

Lahko vam služi: resnična realna spremenljiva funkcija in njegov grafični prikaz

Serije Fourier so še bolj splošne od Taylorjeve serije, saj razvijajo periodične funkcije prekinitve, ki v seriji Taylor nimajo zastopanosti.

Druge oblike serije Fourier

Za analitično razumevanje Fourierove preobrazbe je pomembno.

-Fourierjeva serija na funkciji 2L obdobja

Velikokrat je treba prilagoditi strukturo Fourierjeve serije, na periodične funkcije, katerih obdobje je p = 2l> 0 v intervalu [-l, l].

-Fourierjeva serija v enakomernih in nenavadnih funkcijah

Upošteva se interval [-π, π], ki ponuja prednosti pri izkoriščanju simetričnih značilnosti funkcij.

Če je F navor, je serija Fourier vzpostavljena kot serija Cosenosa.

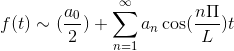
Če je f čuden, je serija Fourierjeva ustanovljena kot niz prsi.

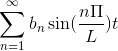
-Kompleksni zapis serije Fourierja

Če imate funkcijo f (t), ki izpolnjuje vse razvite zahteve serije Fourier, jo je mogoče označiti v intervalu [-t, t] z uporabo njene zapletene zapise:

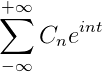
Prijave

Vir: Pexels

Izračun temeljne rešitve

Fourierjeva transformacija je močno orodje pri preučevanju delnih diferencialnih enačb linearnega tipa s konstantnimi koeficienti. Prijavite se za funkcije z domenami, ki niso enakovredno omejene.

Tako kot Laplace Transform, Fourier Transform preoblikuje funkcijo delnih derivatov v navadno diferencialno enačbo veliko lažje za upravljanje.

Cauchyjev problem za toplotno enačbo predstavlja pogosto polje uporabe Fourierove transformacije, kjer je funkcija ustvarjena Dirichlet toplota ali jedro.

Glede izračuna temeljne rešitve so predstavljeni naslednji primeri, kjer je običajno najti Fourierovo transformacijo:

-Laplace enačba

-Enačba toplote

-Schrödingerjeva enačba

-Valovna enačba

Teorija signala

Splošni razlog za uporabo Fourierove preobrazbe v tej veji je večinoma posledica značilne razgradnje signala kot neskončnega prekrivanja lažje obdelanih signalov.

To je lahko zvočni val ali elektromagnetni val, Fourierjeva transformacija ga izraža v preprostih valovih. Ta predstavitev je precej pogosta pri elektrotehniki.

Vam lahko služi: navpična linija

Po drugi strani pa so primeri uporabe Fourierove transformacije na področju teorije signala:

-Težave z identifikacijo sistema. Ustanovljena F in G

-Težava s konsistenco izhodnega signala

-Težave s filtriranjem signala

Primeri

Primer 1

Določite Fourierovo preobrazbo za naslednji izraz:

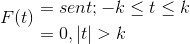
Lahko ga predstavljamo tudi na naslednji način:

F (t) = Greh (t) [h_{(T + K)} - H_{(T - k)} ]

Določen je pravokotni impulz:

p (t) = h_{(T + K)} - H_{(T - k)}

Fourierjeva transformacija se uporablja za naslednji izraz, ki spominja na modulacijsko teorem.

f (t) = p (t) greh (t)

Kje: F [w] = (1/2) I [P (W + 1) - P (W - 1)]

In Fourierjeva preobrazba je opredeljena z:

F [w] =  (1/2) I [(2/2W+1) Sen (K (W+1)) - (2/2W+1) Sen (K (W-1))]

Primer 2

Določite Fourierovo preobrazbo za izražanje:

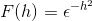Po definiciji izražamo preobrazbo na naslednji način

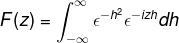
Ker je f (h) enakomerna funkcija, je mogoče potrditi

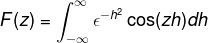Izvajanje v integralu glede na Z je izraz mogoče napisati. Ta korak je pomemben pri delu z diferencialnimi enačbami.

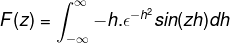
Integracija po delih se uporablja z izbiro spremenljivk in njihovih razlik na naslednji način

u = sin (zh) du = z cos (zh) dh

dv = h (e^-h)²                       V = (e^-h)² / 2

Zamenjava

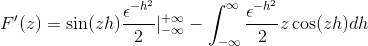
Po oceni v skladu s temeljnim teoremom izračuna

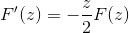
Z uporabo prejšnjega znanja, povezanega z diferencialnimi enačbami prvega reda, je izraz označen kot

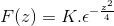
Da dobimo K ocenimo 

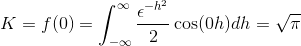
Končno je Fourierovo preoblikovanje opredeljeno kot

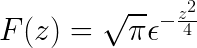
Predlagane vaje

• Določite ekspresijo Fourierjeva transformacija
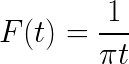
• Rešite naslednji nepravilni integral z uporabo enakosti Pareseval
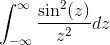
• Pridobite preobrazbo izraza w/(1+w²)

Reference

1. Duoandikoetxea zuazo, j., Fourierjeva analiza. Addison-Wesley Iberoamericana, avtonomna univerza v Madridu, 1995.
2. Levi, j. L., Matematična analiza in numerične metode znanosti in tehnologije. Springer-Verlag, 1990.
3. Lieb, e. H., Gaussova jedrca imajo samo Gaussove maksimizerje. Izum. Matematika. 102, 179–208, 1990.
4. Dym, h., McKean, h. Str., Fourierjeva serija in integrali. Academic Press, New York, 1972.
5. Schwartz, l., Théorie des distribucije. Ed. Hermann, Pariz, 1966.