Tetradecágono

Kaj je tetradecágono?

Tetradecágono je ravno in zaprto geometrijsko figuro 14 strani, ki pripada družini poligonov. Znano je tudi po imenu Tetrakaidecágono, Vse besede, ki izhajajo iz grških besed: "tetra" (cuatri), "kai" (več), "razpadanje" (deset) in "gon" (kot), saj ima tudi 14 notranjih kotov.

Slika prikazuje navaden tetradagon, torej tisti, katerega strani in notranji koti imajo enak ukrep, ki prikazuje glavne značilnosti te številke.

Slika 1.- Redni tetrade z glavnimi lastnostmi. Vir: f. Zapata.

Elementi Tetradecágono

• Strani: Imenujejo jih 14 linijskih segmentov, ki so zaprti za oblikovanje številke. Vsi imajo lahko enako dolžino, v tem primeru je poligon reden ali pa je lahko drugačen, potem pa je nepravilna tetrada.
• Točke: To so presečišča med zaporednimi segmenti in Tetradecágono ima 14 točk.
• Center: Enako oddaljena točka točk.
• Radio: segment, ki združuje center z vrhom.
• Notranji kot: Nastane ga v notranjosti slike in med dvema zaporednima ali sosednjima segmentoma. Ukrepi 154.286 ° za običajni tetradecágon, ne glede na velikost strani.
• Zunanji kot: oblikovana med eno stranjo in podaljšanje ene od sosednjih strani. Ne glede na stransko dolžino ta kot meri 25.7143 ° za navadno tetrade.
• Osrednji kot: Tisti, ki ima svoj vrhov, ki sovpada s središčem poligona in njenih straneh, sta dva zaporedna radijska sprejemnik.
• Diagonala: segment, ki povezuje dve nesorazmerni točki.

Kako je tetradecágono?

Redni poligoni N strani, ki so zgrajeni s pravilom in kompasom, imajo n obrazca 2^r str₁… P_k, biti p_Yo Fermat Primo številke različno in posledično se oblikujejo Fermatove glavne številke 2ⁿ + 1.

Vam lahko služi: do vrstice: formula in enačbe, zastopanost, primeri

Tetradecágono ima n = 14 strani, vendar 14 = 7 × 2, ki niso fermat bratranci, ker jih ni mogoče izraziti na naveden način. Zato ta poligon ne priznava natančne konstrukcije s pravilom in kompasom, ampak konstrukcijo, ki se zelo dobro približa z več metodami.

Splošna metoda za gradnjo rednih poligonov

Sledi splošna metoda (ne edina) za izgradnjo rednih poligonov, registriranih v obodu, vključno z navadno tetrade.

Sestavljen je iz delitve navpičnega premera tega oboda na toliko enakih delov, kolikor strani ima poligon, ki jih je treba risati. V primeru Tetradecágono bodo 14 delov, oštevilčeni na sliki 2. To so koraki:

• Narišite navpični premer od A do B.
• Nato narišite polčas, začenši od točke A, odprite kompas s poljubno odprtino in o tem naredite 14 enako razporejenih delitev. Semirrect in njene delitve lahko izstopijo iz oboda.
• Pridružite se znamki 14VA (v modrem na sliki) na koncu polčasa s točko B.
• Če se še naprej pridružite ostalim oznakam v pol -prereationu z ustreznimi točkami na navpičnem premeru (zelene točke).
• S konico kompasa v A in odprtini, ki je enaka merilu premera oboda, se nariše lok. Z istim ukrepom, vendar podpiranje konice v B (točka 14 slike 2) je narisan še en lok, ki je razrezan s prvimi v točkah V in V 'navedeno.

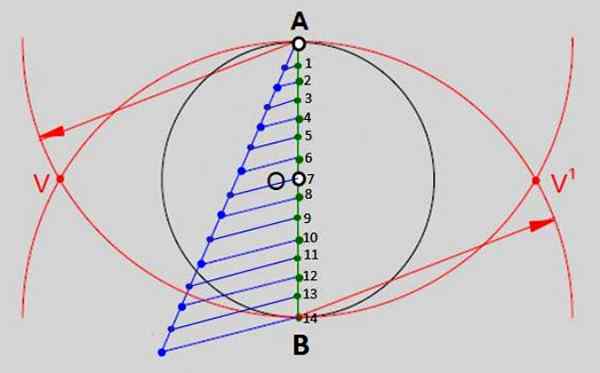Slika 2.- Ena od splošnih metod za izgradnjo rednih poligonov je razdelitev premera oboda na toliko enakih delov, kolikor ima stranice, ki ima poligon. V primeru običajnega tetradeha je 14 enakih delov. Vir: f. Zapata.

• Zdaj s pravilom narišite črto od V 'do točke 2 in jo podaljšajte, da sekate obod v točki C na sliki 3. Označite točko križišča, ki bo ena od vrst slike.

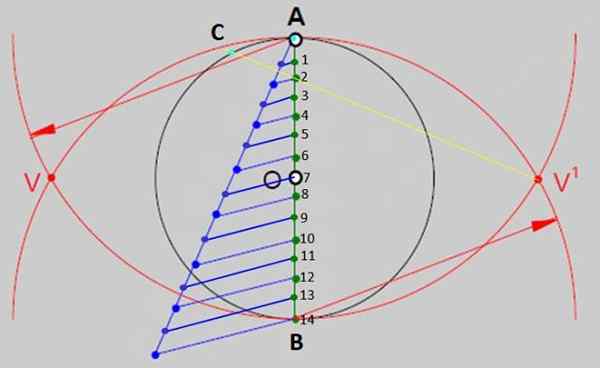Vam lahko služi: statistične veje Slika 3.- AC segment je merilo strani vgrajene tetradecije. Vir: f. Zapata.

• Odprite kompas v izmenični razdalji in podpirajte konico v A ali C, pri čemer črpate loke enakega merila po celotnem obodu, na ta način je razdeljen na približno enake dele, križišča med loki in obodom so vrhovi so Vrtice Tetradecágona.
• S pravilom se pridružite točki s segmenti linij in tvorite stranice poligona.
• Previdno izbrišite pomožne konstrukcije.

V naslednji animaciji je prikazana še ena približna metoda z pravilom in kompasom:

Slika 4.- Animacija, ki prikazuje, kako je narejen tetradecágon (približno redni poligon). Vir: Wikimedia Commons.

Formule za redno tetrade

Naslednje formule veljajo za redne poligone:

• Številka lista: n
• Stranski ukrep: a
• Apotem: l_Do
• Radio: r
• Obod: str
• Območje: a
• Notranji kot: i
• Zunanji kot: e
• Diagonala: d

Znana stran apotema

A = 2l_Do × TG (π/n)

Za n = 14:

A = 2l_Do × TG (π/14)

Znana stran radia

A = 2R × Sen (π/n)

Da n = 14:

A = 2r × sen (π/14)

Znan obod na strani

Obod je vsota strani. Ko je tetradecágono reden:

P = n⋅a = 14⋅A

Če je tetrademágono nepravilen, je treba vse strani dodati neposredno, da dobimo obod.

Znano območje ob strani

A = ¼ na² × COT (π/n)

Za n = 14:

A = ¼ (14²) × COT (π/14) = (7/2) a² × COT (π/14)

Znano območje

A = n⋅l_Do ² × TG (π/n)

Jemanje n = 14 rezultatov:

A = 14L_Do ² × TG (π/14)

Območje, ki temelji na obodu in apotemu

A = (p × l_Do)/2

Vam lahko služi: Bayesovi teorem

Merilo notranjega kota

 Ko je n = 14, notranji kot tetradekagona meri v stopinjah:

I = 12 × 180 ° /14 = 154.286 °

Merjenje zunanjega kota

E = 360 °/N

Ko n = 14 imate:

E = 25.7143 °

Diagonale

Formula za izračun števila diagonalov, prisotnih v katerem koli poligonu, redni ali ne, je:

Za n = 14:

D = 14 × 11/2 = 77 diagonale

Primeri

Še en primer Tetradecágona

Redni poligoni se večkrat pojavljajo v številnih modelih, kot so valute. V primeru rednega tetradagona se to pojavlja v malezijskih spominskih kovancih, ki predstavljajo njene strani za vsako od štirinajstih konfederacijskih držav tega naroda.

Konkavni in konveksni tetradecágonos

Na splošno so lahko poligoni, kot je tetradecágono. Navadni tetradeh je izbočen, tako kot vsak redni poligon, saj kateri koli njegov notranji zorni koti meri 154.286 °.

Po drugi strani pa v konkavnem tetradehu eden ali več njegovih notranjih kotov meri več kot 180 °.

Številčni primer

Glede na navaden tetradagon, katerega stranska meri 5 cm, poiščite:

a) obod
b) Merjenje apotema
c) Dolžina radia
d) Območje

Odgovori

a) Ker gre za navaden poligon, je obod:

P = 14 × 5 cm = 70 cm.

b) iz enačbe a = 2l_Do × TG (π/14), kjer je a = 5 cm, apothem l_Do:

L_Do = a / [2 × tg (π / 14)] = 5 cm / 0.4565 = 21.9064 cm

C) Radio R lahko izračunamo z A = 2R × Sen (π/14):

R = a / [2 × sin (π / 14)] = 5 cm / 0.4565 = 22.4698 cm

d) Za območje je več alternativ, na primer a = (p × l_Do)/2:

A = (70 × 21.9064)/2 cm² = 1533.45 cm².

Reference

1. Aleksander, d. 2013. Geometrija. 5. Izdaja. Cengage učenje.
2. Arturo geometrija. Splošna metoda za risanje poligonov, vpisanih v okolice. Okreval z YouTuba.com
3. Kalkulator juhe. Redni poligonski kalkulator. Obnovljeno od: kalkulatorosoup.com.
4. Risba. Redni poligoni. Okrevano od: risba.com.
5. Requena, b. Konkavni poligon. Okrevano od: univerzeformulas.com.
6. Wikipedija. Gradbeni poligon. Okrevano od: je.Wikipedija.org.