Fizično

Eliptično gibanje

Eliptično gibanje

Kaj je eliptično gibanje?

V eliptičnem gibanju mobilni telefon opisuje elipso, kot to počnejo planeti okoli sonca, lune in umetnih satelitov okoli zemlje.

Sila, ki povzroča to gibanje, je sila gravitacije, osrednja sila. Tovrstne sile so usmerjene proti (ali od) fiksne točke ali, njegov modul pa je odvisen od razdalje do te točke. Če je R razdalja in alir Je enota vektor v radijski smeri, osrednja sila F To je vektorska funkcija obrazca:

F = F (r) alir

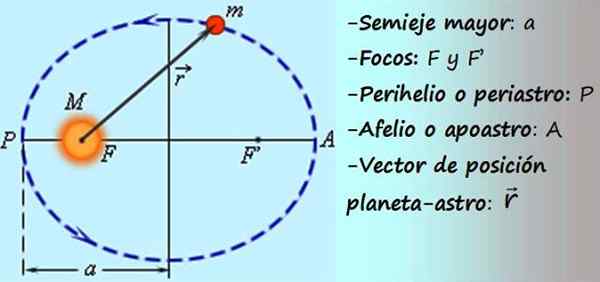
Slika 1. Shema eliptičnega gibanja planeta okoli sonca. Vir: f. Zapata.

Z nekaj matematike je mogoče pokazati, da gibanje predmeta pod delovanjem gravitacije sledi nekaterim od teh štirih poti: elipsa, obod, hiperbola ali prispodoba.

Značilnosti eliptičnega gibanja

Nekatere glavne značilnosti eliptičnega gibanja pod osrednjo silo so:

-Kotni zagon je ohranjen glede na O, imenovan L in to se izračuna skozi vektorski izdelek med vektorji položaja in hitrosti: L = r × mv, Kjer m predstavlja maso mobilnega predmeta.

-Eliptična orbita leži v ravnini, ki jo določajo vektorji r in v.

-Klic izhaja iz kotnega zagona Zakon območij, ki določa, da mobilni potuje enaka območja v enakih časih.

-Mehanska energija je ohranjena tudi v eliptičnem gibanju, če ni disipativnih sil.

-Čas, ki odloži mobilne naprave pri dajanju orbite in skupne energije iste, je odvisen le od dolžine "A" glavnega pol -hexa elipse.

Razlike s krožnim gibanjem

Čeprav se v krožnem in eliptičnem gibanju predmet premika v zaprti in ponavljajoči se poti, torej občasno, obstajajo očitne razlike med enim in drugim in drugim, kot so: na primer:

Lahko vam služi: Norton Theorem: Opis, aplikacije, primeri in vaje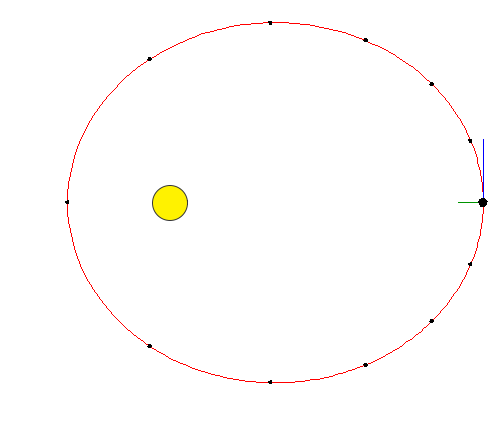Slika 2.- Hitrost je največja, ko je razdalja do sonca minimalna. Vir: Wikimedia Commons.

-V krožnem gibanju mobilni telefon opisuje obod, katerega polmer (razdalja do središča poti) je konstanten, medtem ko v eliptičnem gibanju opisuje elipsa, v kateri je razdalja do središča poti spremenljiva (glej sliko 1).

-V primeru enotnega krožnega gibanja MCU Mobile Barr. To je zakon območij, znan tudi kot Keplerjev drugi zakon planetalnega gibanja.

Pomembne enačbe planetarnega eliptičnega gibanja

Obdobje

V eliptičnem gibanju, ki izhaja iz gravitacijske privlačnosti, je t -obdobje gibanja čas, ki ga potrebuje za planet ali satelit (m), da opiše eliptični krog okoli sonca ali zemlje (m). Z uporabo ohranjanja energije izhaja, da je sorazmerna s kocko dolžine največjega pol -osi elipse:

Kjer je g univerzalna gravitacijska konstanta: 6.67 × 10-enajst N ∙ m2/kg2,   M je masa sonca, zemlje ali objektnega vzroka interakcije na M in "A" je dolžina glavne polose.

Mehanska energija

Skupna energija za sistem planeta (M)- Sonce (M) je:

Kotni zagon

Obseg kotnega zagona na točki eliptične orbite je odvisna tudi od dolžine večje polose, pa tudi do "E" ekscentričnosti, brezdimenzionalnega parametra, ki označuje, kako laska je elipsa. Če je E = 0, elipsa postane obod.

Vam lahko služi: leyden steklenica: deli, delovanje, poskusi

Hitrost

Velikost hitrosti je podana z naslednjo enačbo:

Kjer je R razdalja med točko orbita (lokacija planeta) in fokusom (sonce).

Primeri eliptičnega gibanja

Planetarna gibanja

Keplerjev prvi zakon kaže, da gibanje planetov okoli sonca sledi eliptični poti, s soncem v enem od osvetlitve. Nekateri kometi, ki občasno obiščejo zemljo, na primer Comet Halley, sledijo tudi eliptičnemu gibanju.

Poleg tega eliptičnega translacijskega gibanja in vrtenja okoli svoje osi imajo planeti svoje gibe zaradi zapletenih gravitacijskih interakcij z drugimi nebesnimi planeti in telesi sončnega sistema. Na ta način so gibanja precesije in njut, ki jih ima Zemlja in ki so posledica skupne gravitacijske privlačnosti sonca in lune.

V precesiji osi zemlje opisuje stožec, ko se vrti okoli osi, pravokotne na načrt ali ekliptiko. In v nutaciji, ki prekriva precesijo, os Zemlje niha navzgor in navzdol, ki opisuje eliptično zanko vsakih 18.6 let. Skupno 1385 teh zank v 25767 letih, kar je obdobje precesije zemeljske osi.

Oceanski vodni delček

V oceanskih vodah delček izvaja eliptično gibanje, pri čemer se elipsa vedno bolj laska s povečanjem globine. Po drugi strani, ko so vode globoke, je gibanje delcev krožno.

Kar se zgodi, je, da ko se val približa obali, se sile trenja pojavijo zahvaljujoč bližini dna in to trenje mora upočasniti gibanje v spodnjem delu poti, medtem ko greben nadaljuje svoje gibanje.

Vam lahko služi: enotno pravokotno gibanje: značilnosti, formule, vaje

Rezultat tega je, da je obod založen, učinek pa je poudarjen, ko se globina povečuje.

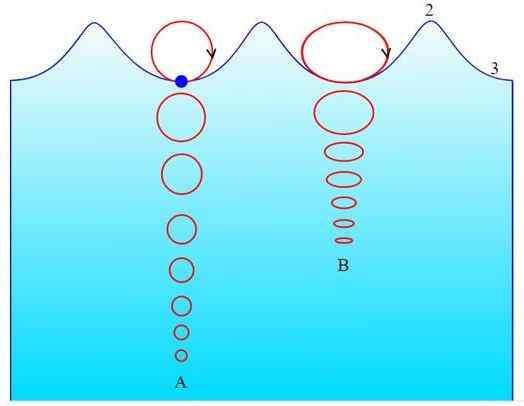Slika 3. Gibanje oceanskih valov v: a) globoke vode in b) površinske vode. Vir: Wikimedia Commons.

Način eliptičnega nihanja v fizičnem nihalu

Fizično nihalo je sestavljeno iz toge trdne snovi, ki lahko niha v ravnini okoli osi, pravokotne nanjo. Če se objekt lahko premika s polno svobodo, lahko opišete kateri koli kot okoli osi, ki združuje sredino mase s točko vzmetenja, in se vrti okoli njega.

Zahvaljujoč vrtenju zemlje lahko nihalo opiše orbite približno eliptično, ki so znane kot način eliptičnega nihanja, za katerega je značilen kotni zagon, ki se razlikuje od 0.

Obstajajo tudi raven način (kotni zagon) in stožčasti način (različen kotni trenutek.

Eliptična kolesa

Eliptična gibanja, opisana prej, se pojavljajo v naravi, vendar jih je mogoče uporabiti tudi za izdelavo koristnih pripomočkov, kot so eliptična kolesa, ki so zelo priljubljeni stroji za izvajanje aerobnih vaj.

So fiksna kolesa, ki so v bistvu sestavljena iz krmila in dveh stopalk, ki jih oseba deluje pri promociji s svojo težo, in z nogami opisujejo elipse. To je naravno in nizko gibanje udarcev, ki je koristno, saj premika številne mišične skupine po telesu.

Reference

  1. Astronomija za vse. Precesija in matica. Okrevano od: astronomiapararatodos.com.
  2. Izračun hitrosti v eliptični orbiti. Okrevano od: foruma.Lawebdefisica.com.
  3. Fowler, Michael. Eliptične orbite: poti do planetov. Okreval od: Galileo.Phys.Virginija.Edu.
  4. Hernández, J. Študij nihajnih načinov na simetričnem fizičnem nihanju z uporabo učinkovitega potenciala. Okreval od: scielo.org.co.
  5. Kittel, c. 1973. Mehanika. Tečaj fizike Berkeley. Zvezek 1. Ed. Sem se obrnil.
  6. Eliptična orbita pod delovanjem osrednje sile. Pridobljeno iz: sc.Ehu.je.
  7. Konzervativni sistemi. Okrevano od: dfmf.Need.je.Wikipedija. Eliptična orbita. Pridobljeno iz: v.Wikipedija.org.