Matematika

Značilnosti teseladosa, tipi (redni, nepravilni), primeri

Značilnosti teseladosa, tipi (redni, nepravilni), primeri

The Tesselled So površine, ki jih pokriva ena ali več figur Tessels. Povsod so: v ulicah in zgradbah vseh vrst. Tessel ali ploščice so ravni kosi, običajno poligoni s kongruentnimi ali izometričnimi kopijami, ki so nameščeni po običajnem vzorcu. Na ta način ni prostorov, ne da bi bili pokriti in se ploščice ali mozaiki ne prekrivajo. 

V primeru, da se uporablja ena vrsta mozaika, ki jo tvori navadni poligon navadni tesseld, Če pa se uporabljata dve ali več vrst običajnih poligonov, je to a Polregularni tesselled.

Slika 1. Nepravilna tla ploščic, ker so pravokotniki neregularni poligoni, tudi ko so kvadratki. Vir: Pixabay.

Končno, ko poligoni, ki tvorijo tesseldo, niso redni, zato je nepravilno tesselled.

Najpogostejša vrsta Tesselda je tista, ki jo tvorijo pravokotni in še posebej kvadratni mozaiki. Na sliki 1 imamo dober primer.

[TOC]

Zgodovina Teseladosa

Tessellation se že tisoč let uporablja za pokrivanje tal in stene palač in templjev različnih kultur in religij.

Na primer sumerska civilizacija, ki je cvetela okoli 3500 do.C. Južno od Mezopotamije, med rekami Evfrat in Tigris, so tesele uporabili v svoji arhitekturi.

Slika 2. Teselados sumerios na vratih istarja. Vir: Wikimedia Commons.

Tesels so vzbudili tudi zanimanje za matematike vseh časov: začenši z Archimedesom v tretjem stoletju pred našim štetjem, sledila je Johannes Kepler leta 1619, Camille Jordan leta 1880.

Lahko vam služi: frakcija, enakovredna 3/5 (rešitev in razlaga)

Penrose je ustvaril neperiodično tessellacijo, znano kot Penrose Tessellation. Inte To je le nekaj imen znanstvenikov, ki so veliko prispevali o tessellu.

Navadni tesel

Navadni teslata je narejena z eno samo vrsto običajnega poligona. Po drugi strani pa mora Tesseldo šteti za redno vse točke letala:

-Pripadajo notranjosti poligona

-Ali do roba dveh sosednjih poligonov 

-Končno lahko pripada skupni točki vsaj treh poligonov.

Z zgornjimi omejitvami je mogoče dokazati, da lahko samo enakostranični trikotniki, kvadratki in šesterokotniki tvorijo navadno tessel.

Nomenklatura

Obstaja nomenklatura za označevanje TESEL - strani.

Ta nomenklatura velja za redne in polregularne tesselve. 

Primer 1: Trikotni teselado

Slika 3 prikazuje trikotno navadno ploščico. Treba je opozoriti, da je vsako trikotno vozlišče ploščic skupna točka šestih enakostraničnih trikotnikov. 

Način označevanja te vrste Tesselda je 3.3.3.3.3.3, ki jih označuje tudi s 36.

Slika 3. Trikotni običajni teselado 3.3.3.3.3.3. Vir: Wikimedia Commons

Primer 2: kvadratni tessel

Slika 4 prikazuje navadne ploščice, sestavljene samo iz kvadratov. Treba je opozoriti, da je vsako vozlišče ploščic obkroženo s štirimi skladnimi kvadratki. Zapis, ki velja za to vrsto kvadratnih tesselves, je: 4.4.4.4 o izmenično 44

Slika 4. Square Tesseld 4.4.4.4. Vir: Wikimedia Commons.

Primer 3: Šesterokotni Tesseld

V šesterokotni tesselle. Nomenklatura za navadni šesterokotni tesselled je 6.6.6 o izmenično 63.

Vam lahko služi: stožčasti odseki: vrste, aplikacije, primeri Slika 5. Šesterokotni Tesseld 6.6.6. Vir: Wikimedia Commons.

Polregularni tesselled

Sel -regularni ali tessellid Tesels of Archimedes sestavljajo dve ali več vrst rednih poligonov. Vsako vozlišče je obkroženo z vrstami poligonov, ki sestavljajo tesselirano v istem vrstnem redu, in stanje roba, ki je popolnoma deljeno s sosedom, se vzdržuje.

Obstaja osem polregularnih teselov:

  1. 3.6.3.6 (tri-heksagolant Tesselled)
  2. 3.3.3.3.6 (šesterokotni Teslate Romo)
  3. 3.3.3.4.4 (Elongado trikotni teselado)
  4. 3.3.4.3.4 (Romo Square Tesselled)
  5. 3.4.6.4 (Rombi-tri-heksagolant Tesseld)
  6. 4.8.8 (okrnjen kvadratni tesselled)
  7. 3.12.12 (okrnjen šesterokotni Tesseld)
  8. 4.6.12 (okrnjen tri-heksagonski tesseld)

Spodaj je prikazanih nekaj primerov polregularnega teslata.

Primer 4: Tixanoral Teselado

Je tisti, ki je sestavljen iz rednih enakostraničnih trikotnikov v strukturi 3.6.3.6, kar pomeni, da je vozlišče ploščice obkroženo (dokler ne dopolni vrnitve) s trikotnikom, šesterokotnikom, trikotnikom in šesterokotnikom. Slika 6 prikazuje tak tessel.

Slika 6. Tri-heksagonski Tesseld (3.6.3.6) To je primer polregularnega tesselleda. Vir: Wikimedia Commons.

Primer 5: Šestkotni Tesseldo Romo

Tako kot ploščica prejšnjega primera tudi to sestavljajo trikotniki in šesterokotniki, vendar je njegova porazdelitev okoli vozlišča 3.3.3.3.6. Slika 7 jasno prikazuje to vrsto tesselled.

Slika 7. Šesterokotni Tesseldo Romo je sestavljen iz šesterokotnika, obkroženega s 16 trikotniki v konfiguraciji 3.3.3.3.6. Vir: Wikimedia Commons.

Primer 6: Rombi-tri-hexanorna Tessel

To je ploščica, ki je sestavljena iz trikotnikov, kvadratov in šesterokotnikov v konfiguraciji 3.4.6.4, ki je prikazano na sliki 8.

Slika 8. Sel -Regular Tesselled, sestavljen iz trikotnika, kvadrata in šesterokotnika v konfiguraciji 3.4.6.4. Vir: Wikimedia Commons.

Nepravilni tesel

Imenujejo jih nepravilni tesels za tiste, ki jih tvorijo nepravilni poligoni ali redni poligoni, vendar ne izpolnjujejo merila, da je vozlišče vrhovi vsaj treh poligonov.

Lahko vam služi: antiderivativ: formule in enačbe, primeri, vaje

Primer 7

Slika 9 prikazuje primer nepravilnih ploščic, v katerih so vsi poligoni redni in skladni. Nepravilno je, ker vozlišče ni pogosta točka vsaj treh kvadratov in obstajajo tudi sosednji kvadratki, ki ne delijo popolnoma roba.

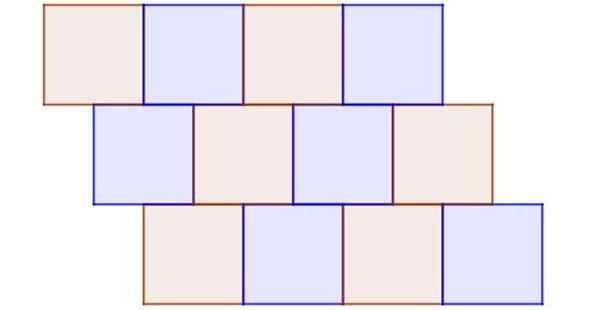Slika 9. Tudi ko so vse ploščice skladni kvadratki, je to jasen primer nepravilnega tesselleda. Vir: f. Zapata.

Primer 8

Paralelogram predloži ravno površino, vendar razen če je kvadrat ne more tvoriti običajnega tessela.

Slika 10. Tesseldo, ki ga tvorijo paralelogrami, je nepravilen, saj so njeni mozaiki neregularni poligoni. Vir: f. Zapata.

Primer 9

Neregularni šesterokotniki z osrednjo simetrijo postavljajo ravno površino, kot je prikazano na naslednji sliki:

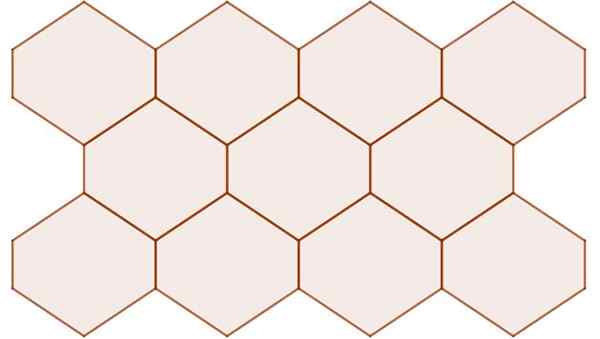Slika 11. Šesterokotniki z osrednjo simetrijo, tudi ko niso redni, so postavili letalo. Vir: f. Zapata.

Primer 10: El Cairo Teselado

To je zelo zanimiva tessellacija, sestavljena iz pentagonov z enakimi dolžinami, vendar z neenakomernimi koti, od katerih sta dva ravna, ostali trije pa 120 °.

Njegovo ime prihaja, da je ta Tesseld v pločniku nekaterih ulic Kaira v Egiptu. Slika 12 prikazuje Tesseldo iz Kaira.

Slika 12. Kairo Tesseldo. Vir: Wikimedia Commons.

Primer 11: Teselado al-Andalus

Tesseldo V nekaterih delih Andaluzije in Severne Afrike sta poleg okrasnih elementov, kot je vegetacija, značilna tudi geometrija in epigrafija. 

Palacios tesselled, kot je alhambra, sestavljena iz ploščic, ki jih tvorijo keramični kosi številnih barv, z več (ne recimo neskončnih) oblik, ki so sprožile geometrijske ploskve.

Slika 13. Teselado Palacio de la Alhambra. Tartaglia / javna domena

Primer 12: Teselado v videoGah

Znana tudi kot tesellation, je eden najbolj razcvetov v video igrah. To je ustvarjanje tekstur za simulacijo Tesselda različnih scenarijev, ki se pojavljajo v simulatorju.

To je jasen razmislek, da se te ovitke še naprej razvijajo s prenosom meja resničnosti.

Reference

  1. Uživajte v matematiki. Tesels. Okrevano od: Uživajte.com
  2. Rubiños. Tesels Rešeni primeri. Okrevano od: matematika.Blogspot.com
  3. Weisstein, Eric W. "Deiregula Tessellation". Weisstein, Eric W, ed. Mathworld. Wolfram Research.
  4. Wikipedija. Tesselled. Okrevano od: je.Wikipedija.com
  5. Wikipedija. Navadni tesseld. Okrevano od: je.Wikipedija.com