Značilnosti trikotnika balacket, lastnosti, formule, območje

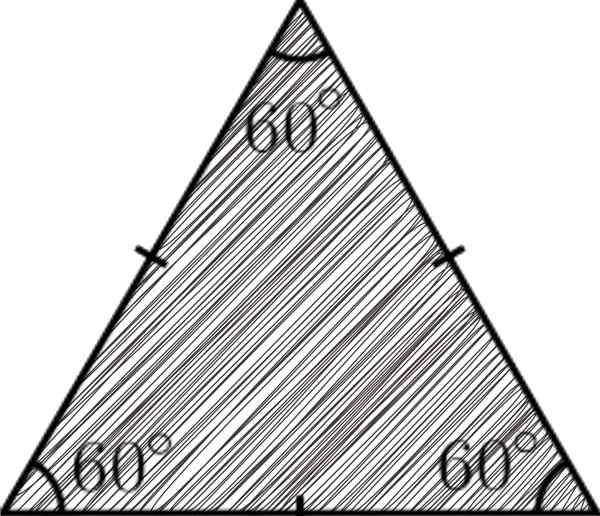
A enakostranični trikotnik Gre za tristranski poligon, kjer so vsi enaki; to pomeni, da imajo isti ukrep. Za to značilnost je dobila ime enakostranično (enake strani).

Trikotniki so poligoni, ki se v geometriji štejejo za najpreprostejše, ker tvorijo tri strani, tri kote in tri točke. V primeru enakostraničnega trikotnika za enake strani pomeni, da bodo tudi njeni trije koti.

Primer enakostraničnega trikotnika

[TOC]

Značilnosti ravnotežnih trikotnikov

- Enake strani

Enakostranični trikotniki so ravne in zaprte figure, sestavljene iz treh linij linij. Trikotniki so razvrščeni po njihovih značilnostih glede na njihove strani in zorne kote; Enakostalni smo razvrstili z meritvijo svojih strani kot parametra, saj so te popolnoma enake, to je, da so skladni.

Enakostranični trikotnik je poseben primer izosceles trikotnika, ker sta dve strani skladni. Zato so vsi enakostranični trikotniki tudi izoscele, vendar ne bodo vsi izosceles trikotniki enakostranični.

Na ta način imajo enakostranični trikotniki enake lastnosti izosceles.

Enakostranske trikotnike lahko z amplitudo njihovih notranjih kotov razvrstimo kot enakostranični akutni trikotnik, ki ima vse tri strani in tri notranje kote z istim ukrepom. Koti bodo akutni, to je manj kot 90^tudi.

- Komponente

Trikotniki imajo na splošno več vrstic in točk, ki ga sestavljajo. Uporabljajo se za izračun območja, strani, kotov, mediane, bisektorja, mediatriksa in višine.

• Mediana: To je črta, ki na eni strani pušča od sredine točke in doseže nasprotno vrhovo. Trije mediji se udeležujejo na točki, imenovani Baricentro ali Centroid.
• Bisektor: To je polčas, ki razdeli kot totov na dva kota enakega merila, zato je znana kot os simetrije. Enakostranični trikotnik ima tri osi simetrije. V enakostraničnem trikotniku je bisektor narisan od točke kota na nasprotno stran in ga razreže v svojo sredino. Ste v točki, imenovani spodbuda.
• Mediatrix: To je segment, pravokoten na stran trikotnika, ki izvira iz sredine tega. V trikotniku so tri mediatike in se strinjajo na točki, imenovani Pokolira.
• Višina: To je črta, ki sega od vrha do strani, ki je nasprotna in tudi ta črta je pravokotna na to stran. Vsi trikotniki imajo tri višine, ki sovpadajo v točki, imenovani Ortotenter.

V naslednjem grafu opazimo trikotnik skale, kjer so podrobno opisane nekatere prej omenjene komponente

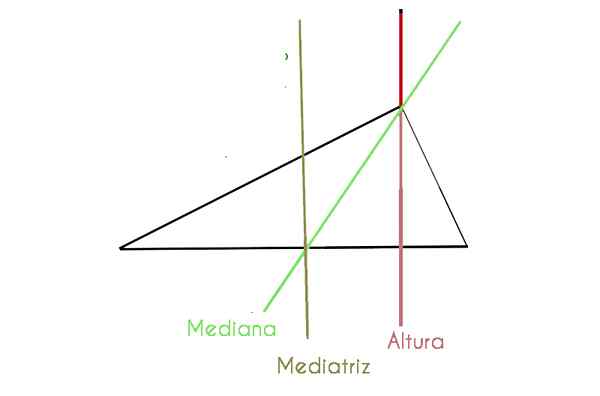Jasno lahko vidimo komponente, nekaj, kar je v enakostraničnem trikotniku težje, saj nekateri sovpadajo. Spodaj jih razložimo:

Bisektor, mediana in mediatrix so naključni

Bisektor se razdeli poleg trikotnika na dva dela. V enakostraničnih trikotnikih bo ta stran razdeljena na dva popolnoma enaka dela, to je, da bo trikotnik razdeljen na dva skladna pravokotnika.

Tako bisektor, narisan iz katerega koli kota enakostraničnega trikotnika.

Vam lahko služi: odnosi s sorazmernostjo: koncept, primeri in vaje

Primer:

Naslednja slika prikazuje trikotnik ABC s srednjo d, ki eno od svojih strani deli na dva segmenta AD in BD.

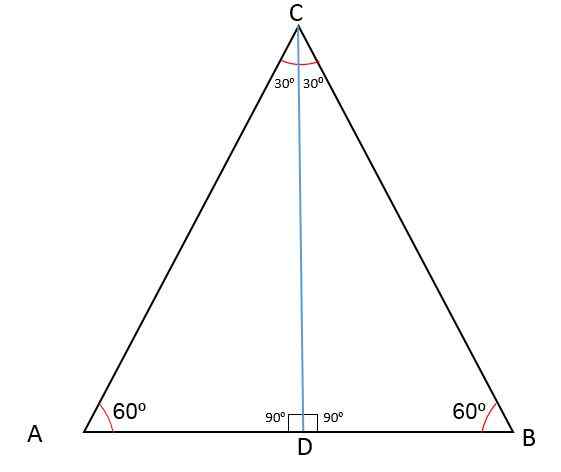
Pri risanju črte od točke D do nasprotne točke po definiciji dobimo mediana CD, ki je glede na tonok C in na stran AB.

Ker segment CD -ja deli trikotnik ABC na dva enaka trikotnika CDB in CDA, to pomeni, da bo to primer skladnosti: stran, kot, stran in s tem tudi CD bisektor BCD.

Pri risanju segmenta CD -ja je kot vrhovni kot razdeljen na dva enaka kota po 30^tudi, Kot vrha A še naprej meri 60^tudi In CD vrstica tvori kot 90^tudi Glede sredine D.

Segment CD tvori kote, ki imajo enak ukrep za ADC in BDC trikotnike, to je, da so dodatni tako, da bo ukrep vsakega:

Med. (ADB) + Med. (ADC) = 180^tudi

2 _* Med. (ADC) = 180^tudi

Med. (ADC) = 180^tudi ÷ 2

Med. (ADC) = 90^tudi.

In tako je segment CD -ja tudi Mediatrix na strani AB.

Bisektor in višina sta naključna

Ko bisektor sledi od točke kota do sredine točke nasprotne strani, to deli enakostranični trikotnik na dva skladna trikotnika.

Na tak način, da se oblikuje kot 90^tudi (naravnost). To kaže, da je ta linijski segment popolnoma pravokoten na to stran in po definiciji bi bila ta črta višina.

Na ta način bisektor katerega koli kota enakostraničnega trikotnika sovpada z višino glede na nasprotno stran tega kota.

Orocentro, Baricentro, Interes in Colecentro Coinsides

Ker višina, mediana, Bisektor in Mediatrix hkrati zastopata isti segment, v enakostraničnem trikotniku seje segmentov -ortocenter, baricenter, spodbuda in obrezovanje -najdemo na isti točki:

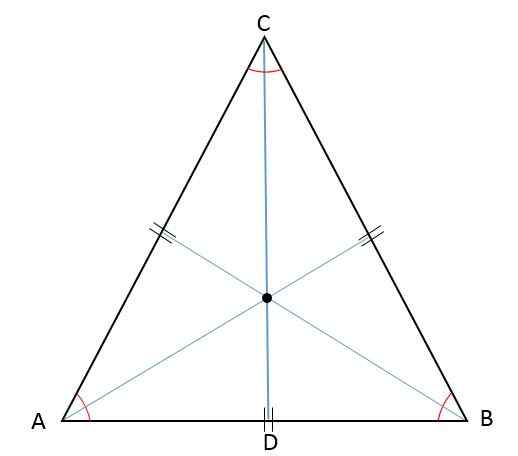
Lastnosti

Glavna lastnost enakostraničnih trikotnikov je, da bodo vedno izosceles trikotniki, saj izoscele oblikujejo dve skladni strani in ravnotežje s tremi.

Na ta način so enakostranični trikotniki podedovali vse lastnosti trikotnika izosceles:

Notranji koti

Vsota notranjih kotov je vedno enaka 180^tudi, In ker so vsi njegovi koti skladni, tako bo vsak od njih izmeril 60^tudi.

Zunanji koti

Vsota zunanjih kotov bo vedno enaka 360^tudi, Zato bo vsak zunanji kot izmeril 120^tudi. To je zato, ker so notranji in zunanji koti dodatni, torej z dodajanjem, da bodo vedno enaki 180^tudi.

Vsota strani

Vsota ukrepov dveh strani mora biti vedno večja od mera tretje strani, torej a + b> c, kjer sta a, b in c meritve na vsaki strani.

Skladne strani

Enakostranični trikotniki imajo svoje tri strani z enakim ukrepom ali dolžino; to pomeni, da so skladni. Zato morate v prejšnjem elementu = B = C.

Skladni koti

Enakostalni trikotniki so znani tudi kot enakomerni trikotniki, saj so njihovi trije notranji koti skladni med seboj. To je zato, ker imajo tudi vse njihove strani enak ukrep.

Lahko vam služi: nominalna spremenljivka: koncept in primeri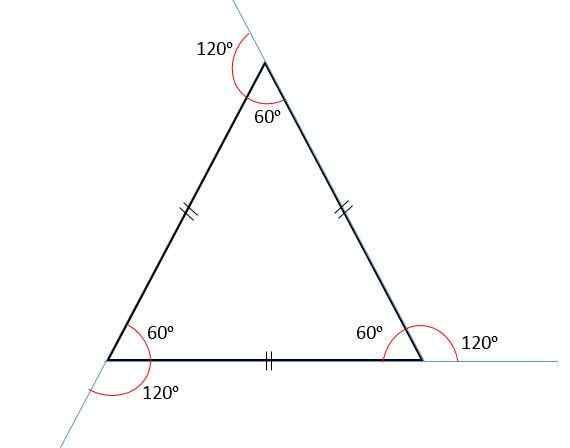

Kako izračunati obod?

Obod poligona se izračuna v vsoti strani. Kot v tem primeru ima enakostranični trikotnik vse strani z istim ukrepom, se njegov obod izračuna z naslednjo formulo:

P = 3 _* stran.

Kako izračunati višino?

Ker je višina črta, pravokotna na podlago, jo deli na dva enaka dela, tako da sega na nasprotni vrhovi. Tako sta dva trikotnika oblikovana enaka pravokotniki.

Višina (h) predstavlja nasprotni kateto (a), polovico AC strani do sosednjega kateta (b) in strani BC predstavlja hipotenuzo (c).

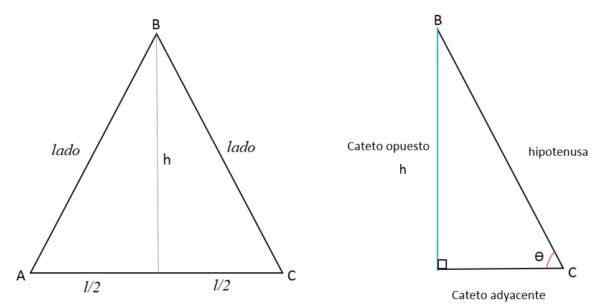
Z uporabo teorema pitagore lahko določimo vrednost višine:

do² + b² = c²

Kje:

do² = višina (h).

b² = stran b / 2.

c² = stran a.

Zamenjava teh vrednosti v teoremu pitagore in čiščenje višine, ki jo imate:

h² + ( l / 2)² = l²

h² +  l²/ 4 = l²

h² = l²  -  l²/ 4

h² = (4_*l² -  l²) / 4

h² =  3_*l² /4

√h² = √ (3_*l² /4)

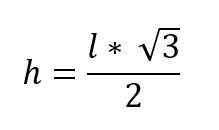
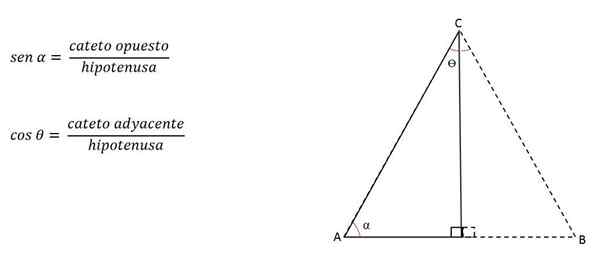
Če je kot, ki ga tvorijo kongruentne strani.

Kategorije se imenujejo nasprotno ali sosednje, odvisno od kota, ki je vzet kot referenca.

Na primer, na prejšnji sliki bo cateto h nasproten kot C, vendar v bližini kota B:

Tako lahko višino izračunamo z:

Kako izračunati strani?

Obstajajo primeri, ko ukrepi na strani trikotnika niso znani, ampak njena višina in koti, ki se oblikujejo v vrhovih.

Za določitev območja v teh primerih je treba uporabiti trigonometrične razloge.

Če poznate kot ene od svojih točk, se identificira kategorija in uporabljen je ustrezen trigonometrični razlog:

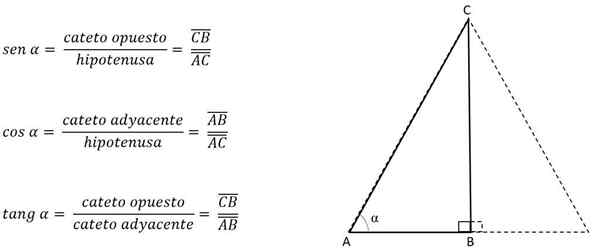
Tako bo Cateto AB nasprotoval kot C, vendar v bližini kota A. Odvisno od strani ali noge, ki ustreza višini, je druga stran očiščena, da dobi vrednost tega, saj ve, da bodo v enakostraničnem trikotniku tri strani vedno imele enak ukrep.

Kako izračunati območje?

Trikotniki se vedno izračunajo z isto formulo, pomnožijo bazo po višini in delijo dva:

Območje = (b _* H) ÷ 2

Vemo, da je višina dana s formulo:

Vaje

- Prva vaja

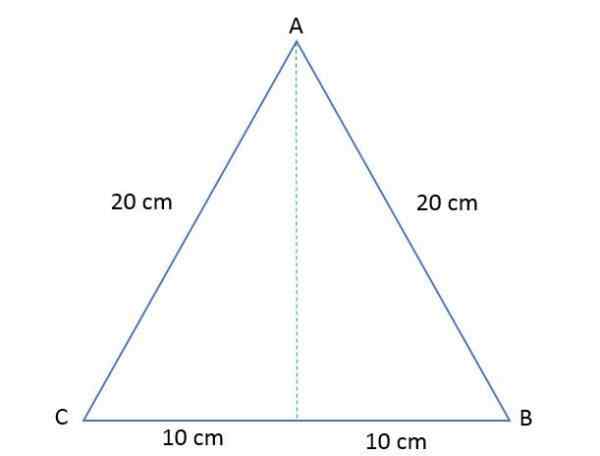
Strani enakostraničnega trikotnika ABC merijo po 20 cm. Izračunajte višino in površino tega poligona.

Rešitev

Za določitev območja tega enakostraničnega trikotnika je treba izračunati višino, saj vemo, da pri risanju trikotnik deli na dva enaka pravokotnika.

Tako lahko uporabite teorem Pythagoras, da ga najdete:

do² + b² = c²

Kje:

A = 20/2 = 10 cm.

B = višina.

C = 20 cm.

Podatki se nadomestijo v teoremu:

10² + b² = 20²

100 cm + b² = 400 cm

b² = (400 - 100) cm

b² = 300 cm

B = √300 cm

B = 17,32 cm.

To pomeni, da je višina trikotnika enaka 17,32 cm. Zdaj je mogoče izračunati dano območje trikotnika z zamenjavo formule:

Območje = (b _* H) ÷ 2

Območje = (20 cm _* 17,32 cm) ÷ 2

Lahko vam služi: linearne transformacije: lastnosti, kakšne so uporaba, tipi, primeri

Območje = 346,40 cm² ÷ 2

Območje = 173,20 cm².

Drug preprostejši način za reševanje vaje je nadomeščanje podatkov v neposredni formuli območja, kjer je vrednost višine tudi implicitno najdena:

- Druga vaja

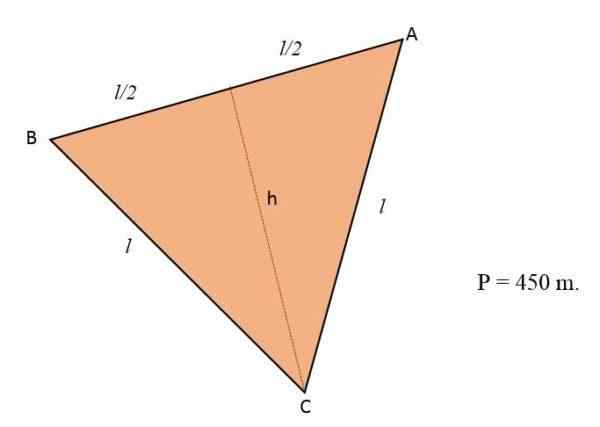
Na polju, ki ima obliko enakostraničnega trikotnika, bodo cvetovi posadili. Če je obod tega terena v višini 450 m, izračunajte število metrov, ki so zasedli cvetje.

Rešitev

Ker vedo, da obod trikotnika ustreza vsoti njegovih treh strani in ker je teren oblikovan kot enakostranični trikotnik, bodo tri strani tega imele enake ukrepe ali dolžino:

P = stran + stran + stran = 3 _* l

3 _* l = 450 m.

L = 450 m ÷ 3

L = 150 m.

Zdaj je treba izračunati le višino tega trikotnika.

Višina razdeli trikotnik na dva skladna pravokotnika trikotnika, kjer ena od kategorij predstavlja višino in drugo polovico baze. Po teoremu s pitagoro je mogoče določiti višino:

do² + b² = c²

Kje:

do = 150 m ÷ 2 = 75 m.

c = 150 m.

b = višina

Podatki se nadomestijo v teoremu:

(75 m)² + b² = (150 m)²

5.625 m + b² = 22.500 m

b² = 22.500 m - 5.625 m

b² = 16.875 m

b = √16.875 m

b = 129,90 m.

Tako bo območje, ki ga bo cvetje zasedlo,:

Območje = B * H ÷ 2

Območje = (150 m _* 129,9 m) ÷ 2

Območje = (19.485 m²) ÷ 2

Območje = 9.742,5 m²

- Tretja vaja

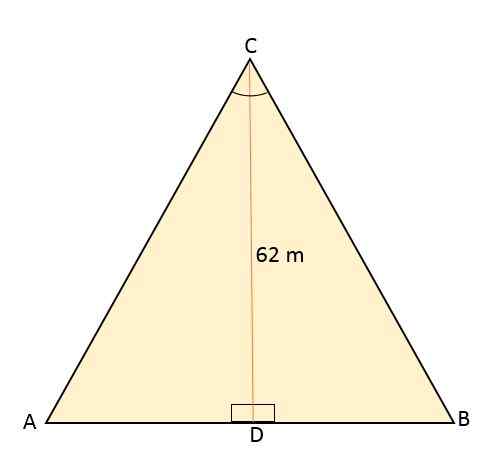
Enakoletalni trikotnik ABC je razdeljen s segmentom črte, ki sega od njene točke C do sredine točke D, ki se nahaja na nasprotni strani (AB). Ta segment meri 62 metrov. Izračunajte območje in obod tega enakostraničnega trikotnika.

Rešitev

Če vemo, da je enakostranični trikotnik razdeljen s segmentom črte, ki ustreza višini, s čimer tvorita dva skladna pravokotnika, to pa tudi kot deli kot vrha C na dva kota z istim ukrepom, 30^tudi vsak.

Višina tvori kot 90^tudi V zvezi s segmentom AB in kotom točke, ki ga nato izmerite 60^tudi.

Nato uporaba kota 30 kot referenca^tudi, Višina CD -ja je vzpostavljena kot cateto, ki meji na kot in BC.

Iz teh podatkov je mogoče določiti vrednost ene od strani trikotnika z uporabo trigonometričnih razlogov:

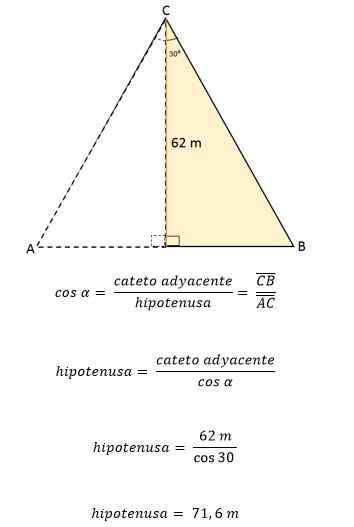
Kot v enakostraničnem trikotniku imajo tudi vse strani popolnoma enake ukrepe ali dolžino, to pomeni, da je vsaka stran enakostraničnega trikotnika ABC enaka 71,6 metra. Če veste, je mogoče določiti vaše območje:

Območje = B * H ÷ 2

Območje = (71,6 m _* 62 m) ÷ 2

Območje = 4.438,6 m² ÷ 2

Območje = 2.219,3 m²

Obod je podan z vsoto njegovih treh strani:

P = stran + stran + stran = 3 _* l

P = 3_*l

P = 3 _* 71,6 m

P = 214,8 m.

Reference

1. Álvaro Rendón,. R. (2004). Tehnična risba: zvezek z dejavnostjo.
2. Arthur Goodman, L. H. (devetnajst devetdeset šest). Algebra in trigonometrija z analitično geometrijo. Pearson Education.
3. Baldor, a. (1941). Algebra. Havana: Kultura.
4. Barbosa, j. L. (2006). Ravna evklidska geometrija. SBM. Rio de Janeiro, .
5. Coxford, a. (1971). Geometrija pristop preobrazbe. ZDA: brata Laidlaw.
6. Euclid, r. Str. (1886). Euclidov elementi geometrije.
7. Héctor Trejo, J. S. (2006). Geometrija in trigonometrija.
8. León Fernández, g. S. (2007). Integrirana geometrija. Metropolitanski tehnološki inštitut.
9. Sullivan, J. (2006). Algebra in trigonometrija. Pearson Education.