Teorem razlagalnega faktorja, primeri, vaje

On Faktorski teorem navaja, da je polinom p (x) deljen z binom oblike (x - a), če je x = a koren p (x), to je p (a) = 0. Govori se, da je polinom deljen med drugim, kadar je njen ostanek ali počitek nič.

Polinom je izraz oblike:

P (x) = a_n xⁿ + do_N-1 x^N-1 +… + A₁ x + a₀

Slika 1. Faktorski teorem. Vir: f. Zapata.

Kje:

-n je stopnja polinoma, ki je največje število celoštevilčnih številk, do katere se dvigne neodvisna spremenljivka x,

-Vrednosti a_n, do_N-1 ,… + A₁ , do₀ So koeficienti polinoma, ki so na splošno resnični številki, lahko pa so tudi zapletene številke.

Polinom stopnje N se lahko razgradi kot produkt oblik binomov:

(X - r_Yo)

Kjer r_Yo To je i-alkish p (x) koren:

P (x) = a_n (X - r₁) (X - r₂)… (X - r_n)

Ker je število korenin polinoma enako stopnji istega.

[TOC]

Primeri

- Primer 1

Razmislite o polinomu po primeru:

P (x) = 3⋅x² - 7⋅x + 2

Želite vedeti, ali je ta polinom deljen po binomialu (x - 2). Če je uporabljen faktorski teorem, moramo oceniti p (x = 2), da vemo, ali je vrednost 2 korenina ali ni. Nato nadaljujemo z oceno izraza:

P (2) = 3⋅22 - 7⋅2 + 2 = 3⋅4 - 7⋅2 + 2 = 12 - 14 + 2 = 12 - 12 = 0.

Izkazalo se je, da je x = 2 p (x) korenina, tako da je v skladu s faktorskim teoremom binom (x - 2) res faktor p (x).

Pojdimo naprej na neposredno preverjanje. Podrobnosti o izdelavi delitve so prikazane na naslednji sliki:

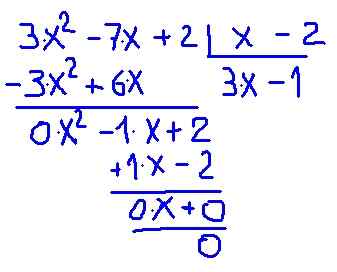Slika 2.- Polinomska delitev P (x) med binom X-2. Vir: f. Zapata.

Preverjeno je, da količnik med p (x) in (x -2) daje polinom manjše stopnje, imenovan količnik c (x) = 3⋅x - 1 z ostankom 0.

Vam lahko služi: vektorske funkcije

Rezultat lahko povzamemo na naslednji način:

(3⋅x² - 7⋅x + 2) ÷ (x -2) = (3⋅x - 1) + 0

Prejšnji izraz lahko zapišemo na drug način, preprosto se spomnimo, da je dividenda P (x) enaka produdu )::

(3⋅x² - 7⋅x + 2) = (x -2) (3⋅x - 1) + 0

Na ta način p (x) polinom (x), torej napišite kot produkt polinomov, originalni polinom: originalni polinom:

(3⋅x² - 7⋅x + 2) = (x -2) (3⋅x - 1)

- Primer 2

Biti polinom q (x) = x³ - x + 2. Želite vedeti, ali je deljiv po binomialu (x + 1).

Najbolj neposreden način je preprosto uporabiti faktorski teorem. V tem primeru morate preprosto preveriti, ali je X = -1 razveljavljen ali ne polinom Q (X).

Nadaljujemo z zamenjavo:

Q (-1) = (-1)³ - (-1) + 2 = -1 + 1 + 2 = 2

Rezultat se razlikuje od nič, zato teorem faktorja zagotavlja, da polinom Q (x) ni deljiv med (x + 1), saj Q (-1) ≠.

Zdaj bo delitev Q (x) narejena med binom (x + 1) kot metodo preverjanja našega sklepa.

Ob tej priložnosti se bo divizija izvedla prek metode sintetične delitve, ki je sestavljena iz postavitve v zgornjo vrsto prve stopnje, vsi koeficienti polinoma, vključno z manjkajočimi.

Potem je v prvem stolpcu postavljen neodvisni izraz delitve, vendar s spremenjenim znakom, v našem primeru je delitelj (x + 1). Njen neodvisni izraz je 1, a kot v prvem stolpcu je postavljen spremenjen znak, to je -1.

Naslednja slika prikazuje, kako se izvaja sintetična delitev:

Vam lahko služi: polinomne enačbe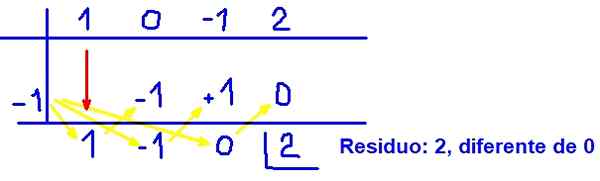Slika 3. Primer polinomne sintetične delitve. Vir: f. Zapata.

S tem rezultatom je dokazano, da (x + 1) ni faktor polinomne q (x) = x³ - x + 2, ker ostanek ni nič.

Ta sklep ni presenečen, ker je bil že napovedan s faktorskim teoremom. Upoštevajte, da je pri zamenjavi x = -1 v q (x), kar dobimo, natančno ostanek ali preostali del polinomne delitve, saj Q (-1) = ostanek = 2.

Seveda oddelek ponuja dodatne informacije količnika C (x) = x² - x.

Če se spomnimo, da je dividenda Q (x) enaka delitvi (x + 1) z razmerjem c (x) plus ostanek r = 2, imamo razširitev polinomnega q (x) na naslednji način:

Q (x) = (x + 1) (x² - x) + 2 = x (x + 1) (x - 1) + 2

Treba je opozoriti, da ta izraz ni faktorizacija omenjenega polinoma, saj obstaja dodajanje ne -nulskega izraza, kar je prav vrednost vrednosti 2.

Vaje

- Vaja 1

Poiščite polinomne dejavnike

P (x) = x³ - 5 x² + 2 x + 8

In tudi napišite svojo faktorizacijo.

Rešitev

Teorem faktorja kaže, da moramo iskati korenine do in nato poiščite dejavnike (x - do), V tem primeru, saj gre za polinom tretje stopnje, morajo biti tri korenine. 

Ker gre za polinom s celotnimi koeficienti, morajo biti korenine med delitev neodvisnega izraza, da je v tem primeru 8. Ti delilniki so:

± 1, ± 2, ± 4, ± 8.

Začnemo z raziskovanjem +1: p (+1) = 1³ - 5⋅ 1² + 2⋅1 + 8 = 1 - 5 + 2 + 8 = 6, ki se razlikuje od 0, zato +1 ni koren.

Raziskujemo -1:

P (-1) = (-1)³ - 5⋅ (-1)² + 2⋅ (-1) + 8 = -1 - 5 - 2 + 8 = 0

Iz rezultata je ugotovljeno, da je -1 koren p (x) y (x -( -1)) = (x + 1) je polinomni faktor.

Vam lahko služi: minimalni kvadratki

Poiskati moramo še dva dejavnika:

Poskusili smo naslednjega, ki je +2:

P (+2) = (+2)³ - 5⋅ (+2)² + 2⋅ (+2) + 8 = 8 + (-20) + 4 + 8 = 0

Spet dobimo nič. Potem je drugi faktor (x - 2).

Ker gre za polinom tretje stopnje, moramo najti le faktor. Zdaj smo poskusili vrednost +4, da bi vedeli, ali polinom prekliče:

P (+4) = (+4)³ - 5⋅ (+4)² + 2⋅ (+4) + 8 = 64 - 80 + 8 + 8 = 0.

Z drugimi besedami.

Ni vam treba še naprej iskati, ker je polinom stopnje 3, ki ima največ tri korenine. V tej vaji so se vse korenine izkazale za resnične in cele.

Zato je polinom P (x) dejavnik, kot je ta:

P (x) = x³ - 5 x² + 2 x + 8 = (x + 1) (x - 2) (x - 4).

- Vaja 2

Biti p⋅x polinom³ - x + 2p. Določite vrednost P za polinom, ki jo je treba deliti (x + 2).

Rešitev

Uporabljamo faktorski teorem, ki navaja, da je, če x = -2 prekliče polinom, potem (x -( -2)) faktor omenjenega polinoma.

Nato X v originalnem polinomu nadomesti (-2), je poenostavljen in enak nič:

P⋅ (-2)³ - (-2) + 2p = 8p + 2 + 2p = 10p + 2 = 0

Zdaj je vrednost P očiščena, tako da se enakost izpolni na nič:

P = -2 / 10 = -⅕ 

To pomeni, da je polinom: 

-⅕⋅x³ - X - ⅖

Delo je z (x + 2) ali kaj je enakovredno: (x + 2) je eden od njegovih dejavnikov.

Reference

1. Baldor Aurelio. Algebra. Uredniška skupina Patria.
2. Demana, w. Precáculculo: grafični, numerični, algebraični 7. izd. Pearson Education.
3. Jiménez, r. 2008. Algebra. Dvorana Prentice.
4. Stewart, J. 2006. Predhodno: matematika za izračun. 5. Izdaja. Cengage učenje.
5. Zill, d. 1984. Algebra in trigonometrija. McGraw Hill.