Vsota polinomov, kot je to, primeri, vaje

The Vsota polinomov To je operacija, ki je sestavljena iz dodajanja dveh ali več polinomov, kar ima za posledico drug polinom. Če ga želite izvesti, je treba dodati izraze istega vrstnega reda vsakega polinoma in navesti nastalo vsoto.

Najprej na kratko pregledamo pomen "pogojev istega reda". Polinom nikogar je sestavljen iz vsot in/ali odštevanja izrazov.

Slika 1. Če želite dodati dva polinoma, jih je treba naročiti in nato zmanjšati podobne izraze. Vir: Pixabay + Wikimedia Commons.

Izrazi so lahko izdelki resničnih števil in ene ali več spremenljivk, predstavljenih s črkami, na primer: 3x² in -drug.do²Pr³ So izrazi.

No, pogoji istega reda so tisti, ki imajo isti eksponent ali moč, čeprav imajo lahko drugačen koeficient.

-Pogoji enakega vrstnega reda so: 5x³, √2 x³ in -1/2x³

-Različna naročila Pogoji: -2x^-2, 2xy^-1 in √6x²in

Pomembno je upoštevati, da je mogoče dodati ali odšteti samo izraze istega reda, ki je znana kot zmanjšanje. V nasprotnem primeru je vsota preprosto navedena.

Ko je koncept izraza istega reda razjasnjen, se polinomi dodajo po teh korakih:

-Vrstni red Najprej polinomi, ki jih dodajajo, vse na enak način, bodisi naraščajo ali se zmanjšujejo, torej z močmi od najmanj do največjih ali obratno.

-Dokončati, V primeru manjka nobena moč v zaporedju.

-Zmanjšati Podobni izrazi.

-Navedite Nastala vsota.

[TOC]

Primeri polinomne vsote

Začeli bomo z dodajanjem dveh polinomov z eno samo spremenljivko, imenovano x, na primer polinoma P (x) in Q (x), ki sta jih dala:

P (x) = 2x² - 5x⁴ + 2x -x⁵ - 3x³ +12

Q (x) = x⁵- 25 x + x²

Po opisanih korakih se začne tako, da jih naročite, kar je najbolj običajen način:

P (x) = -x⁵- 5x⁴  - 3x³  + 2x² + 2x +12

Lahko vam služi: vpisan kot kroga: definicija, teoreme, primeri

Q (x) = x⁵+ x² - 25x

Polinom q (x) ni popoln, vidimo, da pooblastila s eksponentom 4, 3 in 0. Slednji je preprosto neodvisen izraz, tisti, ki nima črke.

Q (x) = x⁵+ 0x⁴ + 0x³ + x² - 25x + 0

Ko je ta korak končan, so pripravljeni dodati. Lahko dodate podobne izraze in nato navedete vsoto ali položite polinome, ki jih naročijo drug drugega in na ta način zmanjšate po stolpcih:

- x⁵ - 5x⁴  - 3x³ + 2x² + 2x +12

+ x⁵ + 0x⁴ + 0x³  +  x²  - 25x + 0     +

--

0x⁵-5x⁴ - 3x³  +3x² - 23x + 12 = p (x) + q (x)

Pomembno je opozoriti, da ko dodamo algebraično spoštovanje pravila znakov, na ta način 2x + (-25 x) = -23x. To pomeni, če se koeficienti odštejejo različni znak in rezultat nosi znak glavnega.

Dodajte dva ali več polinomov z več kot eni spremenljivki

Ko gre za polinome z več kot eno spremenljivko, je eden izmed njih izbran za naročanje. Recimo, da se zahteva, da doda:

R (x, y) = 5x²  - 4y² +  8xy - 6y³ 

In:

T (x, y) = ½ x²- 6y²  - 11xy + x³in

Izbran je ena od spremenljivk, na primer X za naročanje:

R (x, y) = 5x² +  8xy - 6y³  - 4y²

T (x, y) = + x³y + ½ x² - 11xy - 6y² 

Manjkajoči pogoji so takoj zaključeni, po katerem ima vsak polinom:

R (x, y) = 0x³in + 5x² +  8xy - 6y³  - 4y²

T (x, y) = + x³y + ½ x² - 11xy + 0y³ - 6y² 

In oba sta pripravljena zmanjšati podobne izraze:

0x³in + 5x² +  8xy - 6y³  - 4y²

Vam lahko služi: koeficient določanja: formule, izračun, razlaga, primeri

+ x³y + ½ x² - 11xy + 0y³ - 6y²       +

-

+ x³Y + 11/2x² - 3xy - 6y³  - 10y²    = R (x, y) + t (x, y)

Vaje polinomne vsote

- Vaja 1

V naslednji vsoti polinomov navedite izraz, ki mora iti v prazno, da dobite polinomno vsoto:

-5x⁴  + 0x³ +  2x²         + 1

x⁵  + 2x⁴             - 21x² + 8x - 3

2x⁵             +9x³             -14x

-

-6x⁵+10x⁴ -0x³  + 5x²   - 11x + 21

Rešitev

Pridobiti -6x⁵ Potreben je izraz oblike sekire⁵, takšno, da:

A + 1+ 2 = -6

Zato:

A = -6-1-2 = -9

In iskan izraz je:

-9x⁵

-Nadaljujte na podoben način, da najdete preostale pogoje. Tu je eksponent 4:

-5 + 2 + a = 10 → a = 10 + 5-2 = 13

Manjkajoči izraz je: 13x⁴.

-Za X Powers³ Takoj je, da mora biti izraz -9x³, Na ta način je koeficient kubičnega izraza 0.

-Kar zadeva kvadratne moči: A + 8 -14 = -11 → A = -11 -8 + 14 = -5 in izraz je -5x².

-Linearni izraz dobimo z A +8 -14 = -11 → A = -11 + 14 -8 = -5, ki je manjkajoč izraz -5x.

-Končno je neodvisni izraz: 1 -3 + a = -21 → a = -19.

- Vaja 2

Obdan je ravno teren, kot je prikazano na sliki. Poiščite izraz za:

a) obod in

b) njegovo območje glede na navedene dolžine:

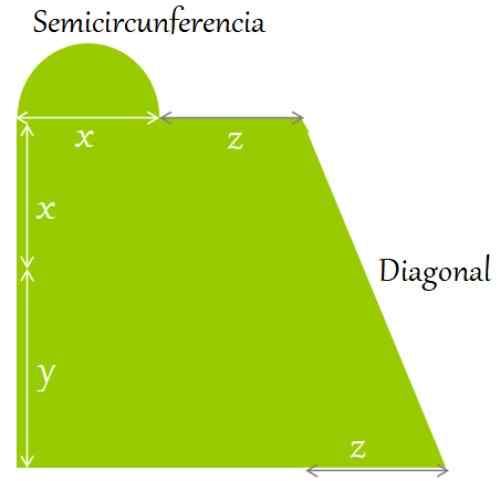Slika 2. Razen teren je obdan z označenimi oblikami in dimenzijami. Vir: f. Zapata.

Rešitev

Obod je opredeljen kot vsota strani in obrisov slike. Začenši v spodnjem levem kotu, v smeri rok ure imate:

Lahko vam služi: Isosceles Trapezoid: Lastnosti, odnosi in formule, primeri

Obod = y + x + polkrog dolžine + z + diagonalna dolžina + Z + z + x

Polkrog ima premer, enak x. Ker je polmer polovica premera, mora:

Radio = x/2.

Formula za dolžino popolnega oboda je:

L = 2π x radio

Tako:

Polkrog dolžina = ½. 2π (x/2) = πx/2

Diagonala se izračuna s teoremom pitagore, nanesenega na stranice: (x+y), ki je navpična stran in z, kar je vodoravno:

Diagonal = [(x+y)² + z²]^1/2

Ti izrazi se nadomestijo v obodu, da dobimo:

Perimeter = y + x + πx/2 + z + [(x + y)² + z²]^1/2+ z + x + z

Podobni izrazi se zmanjšajo, saj vsota zahteva, da se rezultat poenostavi na največ:

Perimeter = y + [x + π (x/2) + x] + z + z + z + [(x + y)² + z²]^1/2 = y + (2 + π /2) x + 3z

Rešitev b

Nastalo območje je vsota območja pravokotnika, polkroga in desnega trikotnika. Formule za ta območja so:

-Pravokotnik: Osnovna višina x

-Polkrog: ½ π (radio)²

-Trikotnik: Osnovna x višina /2

Območje pravokotnika

(x+y). (x+z) = x² + Xz + yx + yz

Podmestno območje

½ π (x/2)² = π x² / 8

Območje trikotnika

½ z (x + y) = ½ zx + ½ zy

Celotna površina

Za iskanje skupne površine se dodajo izrazi za vsako delno območje:

Skupna površina = x² + Xz + yx + yz + (π x² / 8) + ½ zx + ½ zy

In končno vsi podobni izrazi:

Skupna površina = (1 + π/8) x² + 3/2 xy + 3/2yz + yx

Reference

1. Baldor, a. 1991. Algebra. Venezuelski kulturni uvodnik s.Do.
2. Jiménez, r. 2008. Algebra. Dvorana Prentice.
3. Matematika je zabavna. Dodajanje in odštevanje polinomov. Okrevano od: matematika.com.
4. Inštitut Monterey. Dodajanje in odštevanje polinomov. Okreval od: montereyinstitute.org.
5. UC Berkeley. Algebra polinomov. Okrevano od: matematika.Berkeley.Edu.