Revolution Solid Tads Volume, vrste, rešene vaje

On Revolucija trdna To je tridimenzionalna figura, ki nastane z vrtenjem ravne površine okoli osne osi ali osi revolucije. Slika 1 prikazuje animacijo trdne revolucije, ustvarjene na ta način.

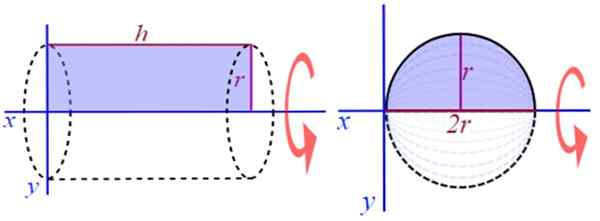
Drug zelo enostaven primer za vizualizacijo je ustvariti ravno krožni valj, vrtenje pravokotnika višine ali dolgega H in radia R okoli pozitivne osi X (slika 2). Če želite najti svojo glasnost, obstaja dobro znana formula:

V = osnovno območje x višina

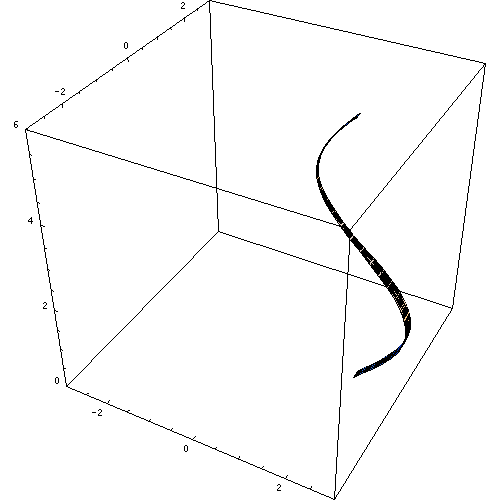Slika 1. Slika, ustvarjena z vrtenjem krivulje sen x. Vir: Wikimedia Commons. Macks/cc by-sa (https: // creativeCommons.Org/licence/by-sa/2.5).

Druge revolucijske trdne snovi so krogla, ravni krožni stožec in različne figure, glede na površino, postavljeno v vrtenje, in seveda izbrana osi.

Slika 2. Generacija ravnega krožnega valja in krogle. Vir: Wikimedia Commons.

Na primer, vrtenje polkroga okoli črte, vzporedno s premerom.

Za valj, stožec, kroglo, tako masivo in luknje obstajajo formule za iskanje volumna, ki je odvisna od polmera in višine. Ko pa jih ustvarijo druge površine, se glasnost izračuna z določenimi integrali.

[TOC]

Vrste revolucijskih trdnih snovi

Revolucijske trdne snovi je mogoče razvrstiti po krivulji, ki jih ustvari:

Kroglo

Dovolj je, da vrtimo polkrog okoli osi, ki bo premer radijske krogle. Njegova glasnost je:

V_kroglo = (4/3) πr³

Muca

Za pridobitev H in radijskega stožca, površine, ki mora. Njegova glasnost je:

V_Muca = (1/3) πhr²

Valj

Vrtenje pravokotnika okoli osne osi, ki poteka skozi ene strani, ki je lahko kratka ali dolga stran, dobimo ravno krožni cilinder polmera r in višino H, katere prostornina je:

Vam lahko služi: vrv (geometrija): dolžina, izrek in vaje

V_valj = πr²H

Toroid

Bik ima obliko krofa. Dobimo ga z vrtenjem krožnega območja okoli črte v ravnini, ki ne seka kroga. Njegova glasnost daje:

V_Toroid = 2πa²R

Kjer je a polmer preseka in r polmer toroida v skladu s shemo, predstavljeno na sliki:

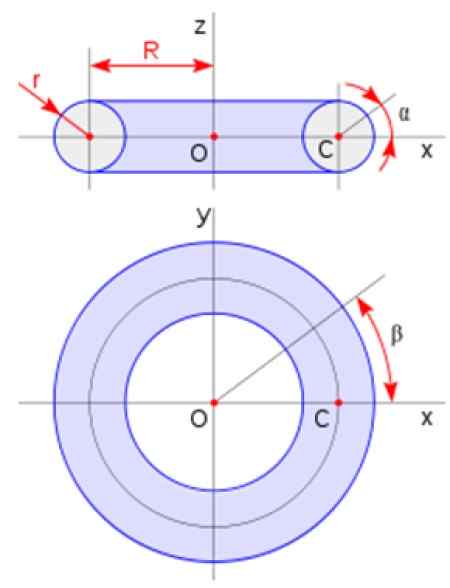Slika 3. Dimenzije toroidov. Vir: Wikimedia Commons.

Metode za izračun volumna revolucijske trdne trdne snovi

V integralnem izračunu sta ti dve metodi pogosti:

-Diski in podložke

-Lupine

Metoda diska ali podložke

Ko je rezina trdne revolucije, je presek lahko album, če je trdna trdna ali pa je lahko nekakšna podložka (album z luknjo na sredini), če je trdna luknja.

Recimo, da se ravno območje vrti okoli vodoravne osi. Iz tega ravnega območja vzamemo majhen Δx širino pravokotnik, ki se pravokotno vrti okoli osne osi.

Višina pravokotnika je med najbolj zunanjo krivuljo r (x) in najbolj notranjimi r (x). Ustrezajo zunanjemu polmeru oziroma notranjega radia.

Pri izdelavi tega vrtenja se ustvari ΔV volumna podložka, ki jo daje:

ΔV = celotna glasnost - količina luknje (če obstaja)

Spominjamo se, da je prostornina ravnega krožnega valja π. radio² X višina, imamo:

ΔV = π [r²(x) - r²(x)] Δx

Trdno snov lahko razdelimo na množico majhnih delov volumna ΔV. Če jih vse dodamo, bomo imeli celotno glasnost.

Da bi to storili.

Lahko vam služi: medsebojno izključni dogodki: lastnosti in primeri

Tako imamo integral:

V = ∫_do^b π [r²(x) - r²(x)] dx

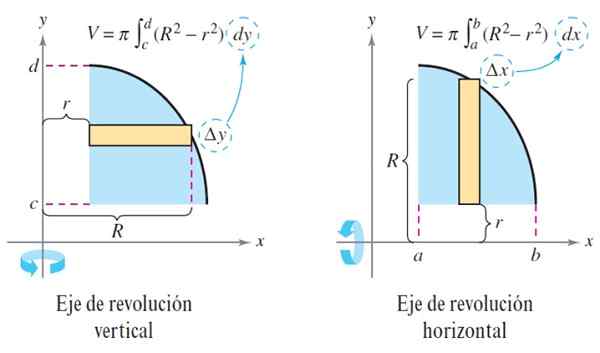Slika 3. Metoda podložk. Vir: Larson. R. Izračun.

V primeru, da je trdna trdna trdna, potem je funkcija r (x) = 0, rezina ustvarjene trdne snovi je disk in volumen ostane:

V = ∫_do^b πr²(x) dx

Ko je revolucijska os navpična, so v obliki prejšnje enačbe:

V = ∫_do^b π [r² (Y) - r² (y)] dy in v = ∫_do^b πr²(Y) dy

Plast

Kot poudarja ime, je ta metoda domnevati, da je trdna snov sestavljena iz diferencialnih debelih plasti. Plast je tanka cev, ki izvira iz zavoja pravokotnika vzporedno z osi vrtenja.

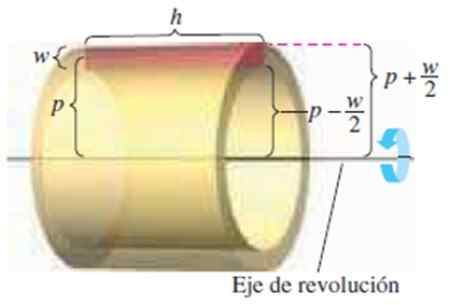Slika 4. Cilindrična plast višine 2, dolga h in polmer p. Vir: Larson, r. Izračun.

Imamo naslednje dimenzije:

-Višina pravokotnika W

-Njegova dolžina h

-Razdalja od središča pravokotnika do rotacijske osi str

Vedoč, da je prostornina plasti Zunanji volumen - notranjost prostornine:

π (p + w/2)²H - π (p - w/2)²h

Pri razvoju pomembnih izdelkov in poenostavitve se pridobi:

Prostornina plasti = 2π⋅p⋅w⋅H

Zdaj pa naredimo višino w pravokotnika Δy, kot je razvidno iz naslednje slike:

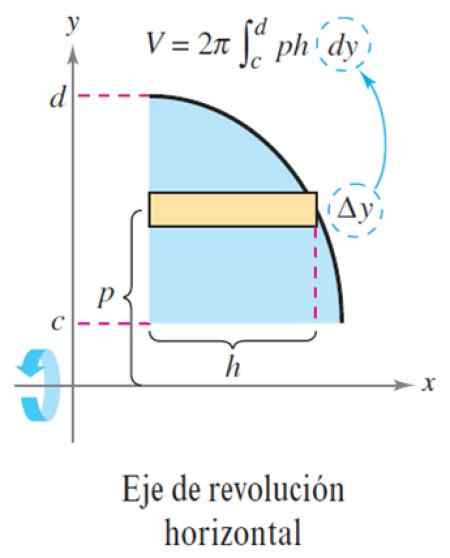Slika 5. Metoda osi horizontalne revolucije. Vir: Larson, r. Izračun spremenljivke.

S tem je glasnost Δv:

ΔV = 2π p x h x Δy

In izdelava števila plasti n Biti zelo velik, Δy postane diferencialni dy, tako da je celotna glasnost integral:

V = ∫_c^d 2π p (y) h (y) dy

Opisani postopek se uporablja podobno, kadar je revolucijska os navpična:

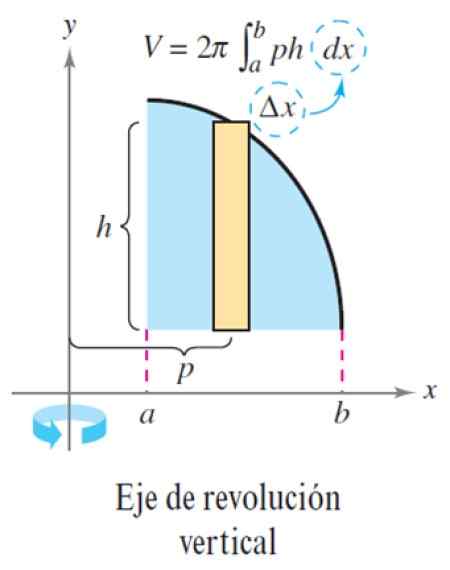Slika 6. Metoda plasti za osi navpične revolucije. Vir: Larson, r. Izračun spremenljivke.

Vaja rešena

Poiščite prostornino, ustvarjeno z vrtenjem ravnega območja med krivuljami:

y = x²;  y = 0; x = 2

Okoli osi in.

Vam lahko služi: negativna homotecia

Rešitev

-Prva stvar je graditi regijo, ki bo ustvarila revolucijo trdno in poudarila osi obračanja. Imamo ga v naslednjem grafu:

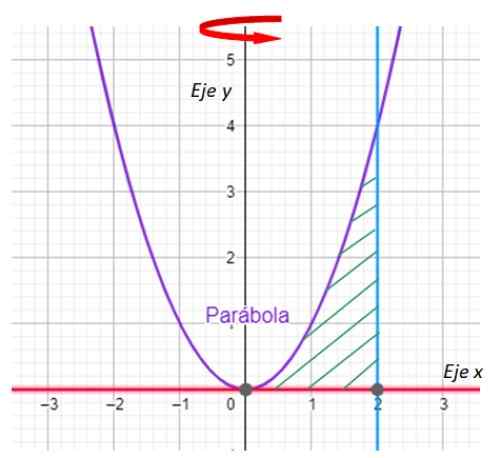Slika 7. Graf krivulj za rešeno vajo. Vir: f. Zapata z geogebro.

-Zdaj se iščejo križišča med krivuljo y = x² in vrstica x = 2. V svojem delu je črta y = 0 nič drugega kot osi x.

Zlahka je opozoriti, da se prispodoba in črta sekata na točki (2,4), ki je podkrepljena z zamenjavo x = 2 na y = x².

-Nato se izbere ena od metod za izračun volumna, na primer metoda plasti z osi navpične revolucije:

V = ∫_do^b 2π p (x) h (x) dx

1. korak: Narišite pravokotnik

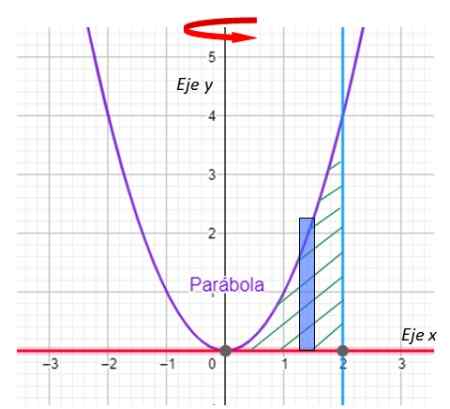Slika 8. Pravokotnik za rešeni primer. Vir: f. Zapata z geogebro.

Pomembno: V metodi plasti je dolga stran pravokotnika vzporedna z rotacijsko osi.

2. korak: Določite P (x)

Plast plasti je x

3. korak: Določite H (x)

Višina pravokotnika določa prispodoba x².

4. korak: Vzpostavite in rešite integral prostornine

Spremenljivka integracije je x, ki se giblje med 0 in 2, s tem imamo omejitve integracije. Zamenjava izrazov za p (x) in h (x)

 Nekatere vaje je mogoče rešiti z obema metodama. Ali lahko bralec to reši z metodo podložk?

Reference

1. Larson, r. 2010. Izračun spremenljivke. 9na. Izdaja. McGraw Hill.
2. Purcell, e. 2007. Izračun z analitično geometrijo. 9na. Izdaja. Pearson Education.
3. Wikipedija. Trdna revolucija. Pridobljeno iz: v.Wikipedija.org.
4. Wikipedija. Toroid. Okrevano od: je.Wikipedija.org.
5. Wolfram Mathworld. Trdna revolucija. Okreval od: Mathworld.Wolfram.com.