Rešene aplikacije, primeri in vaje Fourierjeve serije

The Fourierjeva serija Sestavljeni iz vsote neskončnih izrazov, ki so sestavljeni iz harmoničnih funkcij, sinusa in kosinusa, katerih argument je celoten temelj temeljne frekvence.

Sinusne in kosinusne funkcije se pomnožijo s koeficienti vrednosti, tako da je vsota enaka funkcijam z obdobjem T, ki je enaka dvakrat PI (2π), deljeno s temeljno kotno frekvenco ω ω.

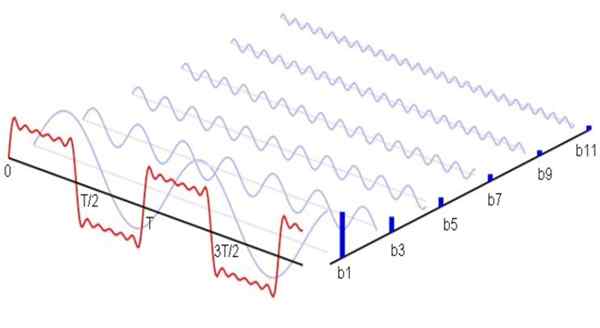
Slika 1. Tu so (v modri barvi) prva ne -nulska harmonika serije Fourierjeva, ki ustreza signalu kvadratne valovne oblike. Vsota teh harmonikov povzroči rdeči signal. Vir: Wikimedia Commons.

Matematično bi bilo izraženo na naslednji način: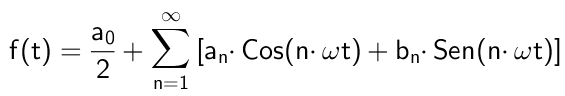

Kje Ω To je temeljna frekvenca, ki je povezana z obdobjem T funkcije f (t) Skozi razmerje: 

Ω = 2π / t

Za periodično obdobje T, funkcija f (t) izpolnjuje to stanje:

f (t) = f (t + k t)

Kje k Je celo število in koeficienti₀ , do_n in b_n Imenujejo se Fourierjevi koeficienti.

[TOC]

Pomembnost in uporaba serije Fourierja

Ime serije Fourier je posledica dejstva, da je bil njegov odkrivalec francoski matematik.

To odkritje je bilo temeljno za matematiko, saj če ima diferencialna enačba določeno harmonično rešitev, je mogoče doseči splošno rešitev s prekrivanjem ali vsoto istega vsote.

Fourierjevi koeficienti periodične funkcije, imenovani tudi znak, So spekter istega.

Zato je spekter niz frekvenc, ki sestavljajo signal, za katerega je značilna amplituda vsake frekvence, ki ustreza vrednostim Fourierovih koeficientov.

Sistemi za stiskanje signala ali zvočne in video valovne oblike, v zadnjem delu bistveno manjše število bitov kot originalni digitalizirani signal.

Fourierjeva serija signala je kot njegov prstni odtis, v smislu, da poznate koeficiente, ki ga sestavljajo, vedno lahko veste, kateri znak jim pripada.

Čeprav je uporaba serije Fourierjeva ali njena najbolj splošna oblika Fourier transformacija, Kot metoda stiskanja signala je bila znana že kar nekaj časa, njegova uporaba v praksi je morala čakati, da numerični procesorji dovolj hitro, kar je omogočilo stiskanje in razgradnjo signalov v "realnem času".

Vam lahko služi: statistične spremenljivke

Primer serije Fourier 

Nato primer funkcije f (t) in njegove serije Fourierja.

Funkcija je:

 f (t) = 0 da 0 ≤ t  < π y 1 si π ≤  t   < 2π

In ima ustrezno serijo Fourierja, ki jo daje:

f (t) = ½ - 2/π⋅se (t) - 2/(3π) ⋅se (3T) - 2/(5π) ⋅sen (5T) - 2/(7π) ⋅sen (7T) -…

Naslednja slika prikazuje funkcijo in delno vsoto serije Fourier:

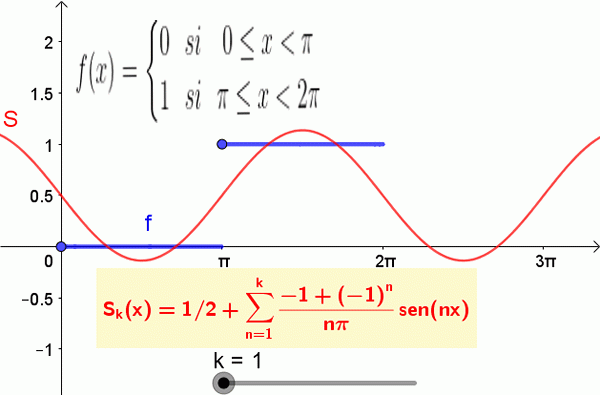Slika 2. Prikazanih je prvih 19 izrazov Fourierove vsote, ki ustrezajo funkciji koraka. Vir: f. Zapata.

Določitev koeficientov

Spodaj je, kako določiti Fourierjeve koeficiente:

Recimo, da je funkcija f (x) definirana v intervalu, ki sega od t_Yo do t_Yo + T, kjer bo kapital obdobje funkcije. Potem je njegova serija Fourierja:

f (t) = a₀/2 + a₁ cos (ω t) + a₂ cos (2 ω t) +… + a_n Cos (n ω t) +…

.. .+ b₁ sin (ω t) +b₂ sin (2 ω t) +… +b_n Greh (n ω t) +..

Izračun neodvisnega izraza

Za iskanje neodvisnega izraza vključimo oba člana enakosti v interval opredelitve funkcije:

[T_Yo , t_Yo+ T]

Zato:

Enako_n ∫Cos (n ω t) dt +…

.. .+ b₁ ∫sen (ω t) dt +b₂ ∫sen (2 ω t) dt +… +b_n ∫sen (n ω t) dt +…

Tukaj simbol ∫ pomeni integral, opredeljen iz t_Yo do t_Yo + T.

Integral prvega izraza je T, ki je pri ocenjevanju v zgornji mejni rezultati:

t_Yo + T

Ko odštejemo spodnjo mejo t_Yo, v dokončnem t.

Vsi drugi izrazi so 0, ker gre za kosinusne ali sinusne funkcije, ocenjene v celotnem obdobju, kot je prikazano spodaj:

∫cos (nω t) dt = (1/ nω) ∫cos (nω t) d (nω t)

Ne pozabite, da simbol ∫ pomeni integracijo med t_Yo do t_Yo + T. 

Za integracijo izrazov, ki imajo kosinus ali dojko, bomo naredili naslednjo spremembo spremenljivke:

x = ω (t - t_Yo)

Torej je diferencial X, DX enak diferencialu D (ωt).

Torej je integral, ki ga je treba izvesti:

Ker je n celo število, potem bo definirani integral vedno dal ničlo. Enako velja za sinusovo funkcijo.

Zato je opredeljen integra, ocenjen v celotnem obdobju vseh izrazov. 

Vam lahko služi: oddelki, v katerih je ostanek 300

Zato je sklenjeno, da se izraz A₀ izračuna na naslednji način:

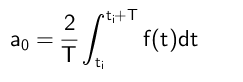
Izračun koeficientov na

Za izračun koeficientov, ki se množijo na kosinusne funkcije, je treba pomnožiti oba člana enakosti:

f (t) = a₀/2 + a₁ cos (ω t) + a₂ cos (2 ω t) +… + a_n Cos (n ω t) +…

.. .+ b₁ sin (ω t) +b₂ sin (2 ω t) +… +b_n Greh (n ω t) +..

S kosinusno funkcijo, ovrednoteno v ustrezni harmoniki in nato integral, opredeljen v celotnem obdobju za oba člana. 

Na primer za izračun_m Oba člana pomnožita COS (Mωt):

f (t) cos (m ω t) = a₀/2 cos (m ω t) + a₁ cos (ω t) cos (m ω t) + a₂ cos (2 ω t) cos (m ω t) +… + do_n Cos (n ω t) cos (m ω t) +…

.. .+ b₁ sin (ω t) cos (m ω t) +b₂ sin (2 ω t) cos (m ω t) +… +b_n Greh (n ω t) cos (m ω t) +..

Nato se vključite v celotno obdobje, torej v intervalu, ki sega od T_Yo do t_Yo + T.

Integral izraza, ki vsebuje A₀. 

Integrali, ki vsebujejo produkt cos (n ω t) cos (m ω t), se prav tako razveljavijo, kadar koli n ≠ m. Samo v primeru, da ima n = m integral:

Vsi izrazi, ki imajo kosinus, pomnoženo sinus, torej tisti, ki jih pomnožijo koeficienti B, ki vsebujejo integrale tipa Sen (n ω t) cos (m ω t) obdobje. 

Od tu je sklenjeno, da:

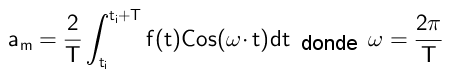
Izračun koeficientov B

Če želite najti koeficiente B, se uporabi podoben postopek, vendar se tokrat tako člana funkcije, ki se ujemata s serijo Fourierja, pomnoži s funkcijo Sen (M ω T).

Iz istih razlogov, ki so že pojasnjeni za primer, v katerem je edini izraz, ki se ne bo razveljavil po vključitvi v celotno obdobje, tisti, v katerem:

n = m

In kjer se pojavi integral [sen (m ω t)]]², ki integrirano v celotnem obdobju povzroči π.

Vam lahko služi: homografska funkcija: kako graditi, rešiti vaje

Na ta način se koeficienti B izračunajo po naslednji formuli:

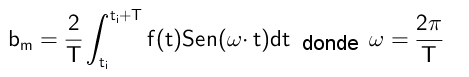
Vaje

- Vaja 1

Naredite izrecni izračun koeficientov funkcije

 f (t) = 0 da 0 ≤ t  < π y 1 si π ≤  t   < 2π

Rešitev

Najprej prepoznamo obdobje T te funkcije kot 2π, tako da je temeljna frekvenca ω = 2π/ t v tem primeru enaka enoti, to je:

Ω = 1

Funkcija je opredeljena v intervalu [0, 2π], zato bodo vse integracije izvedene v omenjenem intervalu. 

Potem se neodvisni izraz izračuna na naslednji način:

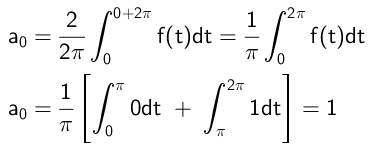
Koeficienti, ki se pomnožijo na kosinusne funkcije, se izračunajo na ta način:

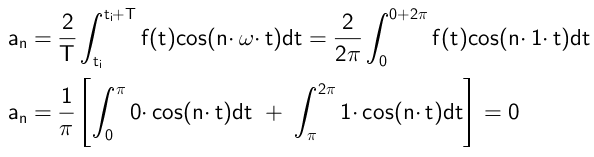
Kot je razvidno, so vsi koeficienti, ki jih je treba, NULL, kar se bo zgodilo pod pogojem, da je funkcija f (t) čudna.

Podobno bodo koeficienti B izračunani na naslednji način:

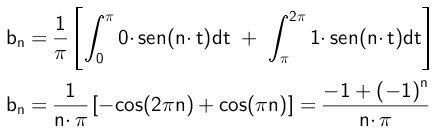
- Vaja 2

Poiščite koeficiente funkcije, ki ustrezajo sliki 1, kar je:

f (t) = -1 da 0≤ t

Rešitev 

Ker funkcija prevzame vrednosti med -1 in +1, lahko intuitiramo, da je neodvisni izraz ničen, vendar ga bomo izrecno izračunali:

Zaradi dejstva, da ima funkcija nenavadno simetrijo, morajo biti vsi koeficienti, ki pomnožijo harmonične izraze s funkcijo kosinusa. Spodaj ga preverimo:

Na koncu bomo našli koeficiente B, ki pomnožijo harmonične izraze, ki vsebujejo funkcijo sinusa:

Kje lahko opazijo vsi izrazi B z UP. Prvi nenavadni izrazi so:

b₁= -4/(π); b₃= -4/(3π); b₅= -4/(5π); b₇= -4/(7π) in b₉= -4/(9π)

https: // youtu.Biti/737YAGWSZYA

Reference

1. Amerror, i. 2013. Obvladovanje diskretne Fourierjeve preobrazbe v eni, dveh ali več dimenzijah: pasti in artefaktov. Springer Science & Business Media.
2. Briggs, w. Devetnajst devetdeset pet. DFT: Priročnik lastnikov za diskretno Fourierovo preobrazbo. Siam.
3. Chu, e. 2008. Diskretne in neprekinjene Fourierjeve preobrazbe: analiza, aplikacije in hitri algoritmi. CRC Press.
4. Guoan Bi, Yonghong Zeng. 2012. Transformacije in hitri algoritmi za analizo in reprezentacije signala. Springer Science & Business Media.
5. Sundararajan, d. 2003. Digitalna obdelava signalov: teorija in praksa.Svetovni znanstveni. 
6. Wikipedija. Fourierjeva serija. Okrevano od: je.Wikipedija.com