Newtonove druge prijave, eksperimente in vaje

The Drugi zakon Newtona o Temeljni zakon dinamike ugotavlja, da če je predmet predmet sile ali nabora sil, ki niso razveljavljene, se bo objekt pospešil v smeri nastale sile in obratno sorazmerno z maso predmeta.

Ja F je neto sila, M Masa predmeta in do Pospešek, ki ga pridobi, potem bi bil Newtonov drugi zakon izražen matematično: do = F / M ali na najbolj običajen način F = M∙do

Pojasnilo Newtonovega drugega zakona. Vir: Self Made.

[TOC]

Pojasnilo in formule

Kot je razloženo zgoraj, je običajni način izražanja drugega zakona s formulo:

F = M∙do

Tako pospeševanje in silo je treba izmeriti iz inercialnega referenčnega sistema. Upoštevajte, da je masa pozitivna količina, zato pospeševalne točke v isti smeri kot posledična sila.

Upoštevajte tudi, da ko je nastala sila nična (F = 0) Potem bo tudi pospešek ničen ( do = 0 ) dokler M> 0. Ta rezultat je v celoti dogovorjen z Newtonovim zakonom ali inercijskim zakonom.

Newtonov prvi zakon vzpostavlja inercialne referenčne sisteme, kot so tisti, ki se premikajo s konstantno hitrostjo glede na prosti delček. V praksi in za namene najpogostejših aplikacij se bo fiksni referenčni sistem na tla ali katerega koli drugega, ki se v zvezi s tem premika s konstantno hitrostjo.

Sila je matematični izraz interakcije predmeta z okoljem. Sila je lahko stalna količina ali se spremeni s časom, položajem in hitrostjo predmeta.

Enota v mednarodnem sistemu (SI) za silo je Newton (N). Masa v (SI) se meri v (kg) in pospeševanju v (m/s²). Newton moči je nujna sila za pospešitev predmeta 1 kg mase pri 1 m/s² .

Rešene vaje

Vaja 1

Predmet mase m se sprosti z določene višine in izmeri pospešek padca 9,8 m/s².

Enako velja za drugo maso mase M 'in še eno maso M "in drugo. Rezultat je vedno pospeševanje gravitacije, ki je označen z G in je vreden 9,8 m/s². V teh poskusih je oblika predmeta in vrednost njegove mase takšna, da je sila zaradi zračnega odpornosti zanemarljiva.

Vam lahko služi: kalcijev fluorid (caf2): struktura, lastnosti, uporabe

Prosimo, da najdete model za kopensko privlačnost (znano kot teža), ki je skladen z eksperimentalnimi rezultati.

Rešitev

Izbrali smo inercialni referenčni sistem (pritrjen glede na tla) s pozitivno smerjo navpične osi x in navzdol.

Edina sila, ki deluje na masni objekt m To je kopenska privlačnost, da se sila imenuje teža Str, Kako kaže navzdol, je pozitivno.

Pospešek, ki ga je pridobil masni objekt m Ko je izdana, je a = g , navzdol in pozitivno.

Predlagamo Newtonov drugi zakon

P = m a

Kakšen bo model P, tako da je pospešek, ki ga napoveduje drugi zakon ? : Edina alternativa je, da je p = m g kadarkoli m> 0.

M G = M A Kjer se razčistimo: a = g

Zaključujemo, da bo teža, sila, s katero zemlja privlači predmet.

P = m∙g

Vaja 2

2 kg bloka mase počiva na popolnoma gladkem in vodoravnem tleh. Če se uporabi 1 N sila, pospeševanje pridobi blok in kakšna hitrost bo po 1 s.

Rešitev

Prva stvar je določiti inercialni koordinatni sistem. Ena je bila izbrana z osi x na tleh in osi ter pravokotno nanjo. Nato je narejen diagram sil, ki postavlja sile zaradi interakcij bloka z okolico.

Sila P predstavlja težo, silo, s katero planet zemlja pritegne blok mase m.

Sila N predstavlja normalno, to je sila navzgor, ki jo površina tal izvaja na bloku m. Znano je, da N ravnotežja točno P, ker se blok ne premika v navpični smeri.

F je vodoravna sila, ki se uporablja za blok M, ki kaže v pozitivno smer osi x.

Neto sila je vsota vseh sil na bloku Mass M. Vsota vektorja F, P in N je narejena. Ker sta p in n enaka in nasprotna, se medsebojno odpovedujeta in neto sila je f.

Tako da bo nastali pospeševanje količnik neto sile med maso:

Lahko vam služi: Mehanska prednost: formula, enačbe, izračun in primeri

a = f / m = 1 n / 2 kg = 0,5 m / s²

Ker se blok začne od preostalega po 1, se bo njegova hitrost spremenila 0 m/s pri 0,5 m/s .

Newtonove druge prijave

Pospešek dvigala

Fant uporablja kopalnico za merjenje teže. Vrednost, ki jo dobite, je 50 kg. Nato fant prevzame težo dvigala svoje stavbe, ker želi izmeriti pospešek začetka dvigala. Rezultati, dobljeni, ko se začne, so:

• Lestvica beleži težo 58 kg za 1,5 s
• Nato znova izmerite 50 kg.

S temi podatki izračunajte pospešek dvigala in hitrost, ki jo pridobite.

Rešitev

Lestvica meri težo v enoti, imenovani Kilogram_fuerza. Po definiciji je kilogram_fuerza sila, s katero planet zemlja privabi predmet 1 kg mase.

Ko je edina sila, ki deluje na predmet, njegova teža, potem pridobi pospešek 9,8 m/s². Torej 1 kg_f je enakovreden 9.8 n.

Teža Str fantka je takrat 50 kg*9.8m/s² = 490 n

Med pospeševanjem lestvica izvaja silo N Na 58 kg_f dečka, enakovredno 58 kg * 9,8 m/s² = 568.4 n.

Pospešek dvigala bo podan z:

A = n/m - g = 568.4 n / 50 kg - 9.8 m/s² = 1.57 m/s²

Hitrost, ki jo je dvigalo pridobilo po 1.5 s z 1 pospeševanjem.57 m/s² je:

v = a * t = 1.57 m/s² * 1.5 s = 2.36 m/s = 8.5 km/h

Naslednja slika prikazuje shemo sil, ki delujejo na fanta:

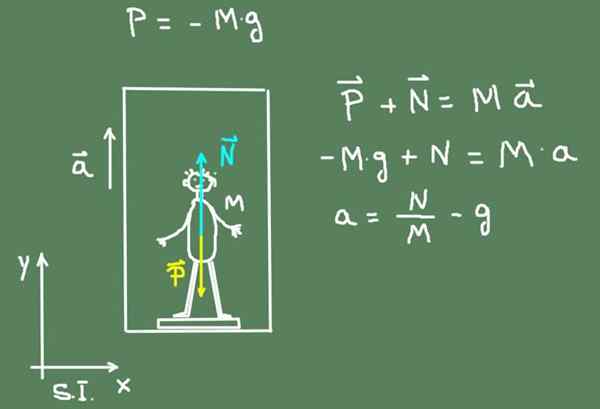
Majonezna steklenica

Otrok prenaša bratovo steklenico bratu, ki je na drugem koncu mize. Za to ga poganja tako, da pridobi hitrost 3 m/s. Ker se steklenica sprosti, dokler se ne ustavi na nasprotnem koncu mize, je bila pot 1,5 m.

Določite vrednost trenja, ki jo tabela izvaja na steklenici, vedoč, da ima maso 0,45 kg.

Rešitev

Najprej bomo določili zavorni pospešek. Za to bomo uporabili naslednje razmerje, ki je že znano za enakomerno pospešeno pravokotno gibanje:

Vf² = vi² + 2 * a * d

kje Vf je končna hitrost, Videl Začetna hitrost, do pospešek in d Premik.

Vam lahko služi: dinamična elektrika

Pospešek, pridobljen iz prejšnjega razmerja, je, kjer je bil premik steklenice jet kot pozitiven.

a = (0 - 9 (m / s) ²) / (2*1.5 m) = -3 m/s²

Neto sila na majonezni steklenici je sila trenja, saj je normalna in teža steklenice uravnotežena: fnet = mraz.

Fr = m * a = 0.45 kg * (-3 m/s²) = -1.35 n = -0.14 kg-f

Otroški poskusi

Otroci in odrasli lahko izvajajo tudi preproste izkušnje, ki jim omogočajo, da preverijo, ali Newtonov drugi zakon resnično deluje v resničnem življenju. Tu sta dve zanimivi dobro:

Eksperiment 1

Preprost poskus zahteva kopalnico in dvigalo. Vzemite težo kopalnice do dvigala in zabeležite vrednosti, ki se označujejo med začetkom vzpona, zagon zagona in v obdobju, ki se premika s konstantno hitrostjo. Izračunajte pospeške dvigala, ki ustrezajo vsakemu primeru.

Eksperiment 2

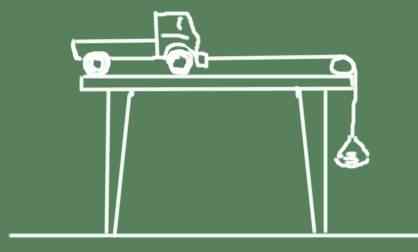
1. Vzemite voziček z igračami, ki imajo kolesa dobro podmazana
2. Držite vrv do skrajnosti.
3. Na robu tabele pritrdite svinčnik ali drug valjast in gladek predmet, na katerem bo prešla vrv.
4. Na drugem koncu vrvi visi majhen koš, na katero bo postavil nekaj kovancev ali nekaj, kar služi za težo.

Shema eksperimenta je prikazana spodaj:

• Spustite voziček in opazujte, kako pospešuje.
• Nato povečajte maso vozička tako, da nanj postavite kovance ali nekaj, kar poveča njegovo maso.
• Recimo, če se pospešek poveča ali zmanjšuje. Na voziček postavite več testa, upoštevajte, kako pospešuje in zaključi.

Potem voziček ostane brez dodatne teže in pusti, da se pospeši. Potem se na košarico postavi več teže, da se poveča sila, ki se nanaša na voziček.

• Primerjajte pospešek s prejšnjim primerom, navedite, ali se poveča ali zmanjšuje. Lahko ponovite dodajanje več teže v koš in opazujete pospešek vozička.
• Navedite, ali se poveča ali zmanjšuje.
• Analizirajte svoje rezultate in povejte, ali se strinjajo z Newtonovim drugim zakonom ali ne.

Zanimivi članki

Primeri Newtonovega drugega zakona.

Newtonov prvi zakon.

Primeri Newtonovega drugega zakona.

Reference

1. Alonso m., Finn e. 1970. Fizika zvezek I: Mehanika. Interameriški izobraževalni sklad s.Do. 156-163.
2. Hewitt, str. 2012. Konceptualna fizikalna znanost. Peta izdaja. 41-46.
3. Mladi, Hugh. 2015. Univerzitetna fizika s sodobno fiziko. 14. izd. Pearson. 108-115.