Ortonormalne bazne lastnosti, primeri in vaje

A Ortonormalna baza Nastavljen je s pravokotnimi vektorji med seboj in katerih modul je vreden tudi 1 (enotni vektorji). Ne pozabite, da baza B v vektorskem prostoru V, Opredeljen je kot niz linearno neodvisnih vektorjev, ki lahko ustvarijo ta prostor.

Vektorski prostor je abstraktna matematična entiteta med tem, katerih elementi so vektorji, na splošno povezani s fizičnimi velikostmi, kot so hitrost, moč in premik ali tudi matrike, polinomi in funkcije.

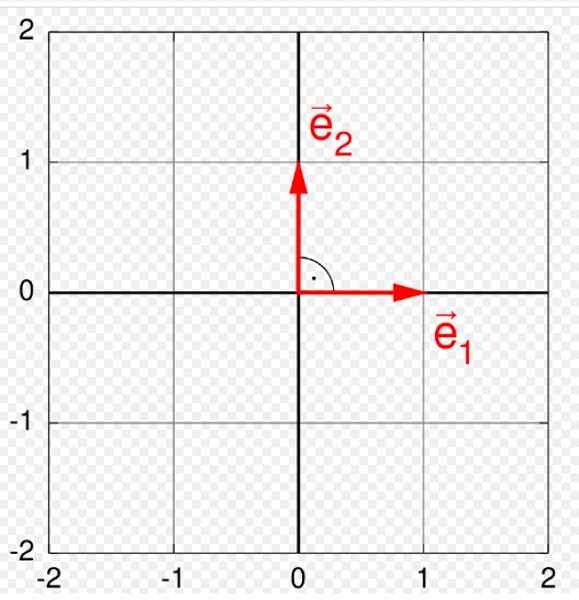
Slika 1. Ortonormalna podlaga v ravnini. Vir: Wikimedia Commons. Quartl [CC BY-SA (https: // createCommons.Org/licence/by-sa/3.0)].

Vektorji imajo tri značilne elemente: velikost ali modul, smer in pomen. Ortonormalna baza je še posebej koristna za predstavljanje in delovanje z njimi, ker kateri koli vektor, ki spada v določen vektorski prostor V, Lahko ga zapišemo kot linearna kombinacija vektorjev, ki tvorijo bazo Ortonormal.

Na ta način se analitično analizirajo operacije med vektorji, kot so vsota, odštevanje in različne vrste izdelkov, opredeljenih v omenjenem prostoru.

Med najbolj uporabljenimi bazami fizike je osnova, ki jo tvorijo enotni vektorji Yo, J in k predstavlja tri značilne smeri tridimenzionalnega prostora: visok, širok in globina. Ti vektorji so znani tudi po imenu Enotni kanonični vektorji.

Če namesto tega vektorji delajo na ravnini, bi bilo dovolj z dvema od teh treh komponenta, medtem ko le ena.

[TOC]

Osnovne lastnosti

1- baza B Je najmanjši možni nabor vektorjev, ki ustvarjajo vektorski prostor V.

2- Elementi B So linearno neodvisni.

3- Vsaka baza B vektorskega prostora V, omogoča izražanje vseh vektorjev V Kot linearna kombinacija tega in ta oblika je edinstvena za vsak vektor. Zato a B Znan je tudi kot Sistem generatorja.

4- Isti vektorski prostor V lahko imajo različne baze.

Vam lahko služi: centrifugalna sila: formule, kako se izračuna, primeri, vaje

Primeri baz

Spodaj več primerov ortonormalnih baz in baz na splošno:

Kanonična osnova v ℜ ⁿ

Imenovana tudi naravna ali standardna baza ℜ ⁿ, Kjer ℜ ⁿ Je prostor n-dimenzionalni, Na primer, tridimenzionalni prostor je ℜ ³. Na vrednost n Se imenuje dimenzija vektorskega prostora in označuje kot Dim (v).

Vsi vektorji, ki pripadajo ℜ ⁿ Zastopajo jih N-ZDA Naročeno. Za prostor ℜⁿ, Kanonična osnova je:

in₁ =; in₂ =; in_n =

V tem primeru smo zapisovali z oklepaji ali "oklepaji" in krepko za vektorje enot in₁, in₂, in₃..

Kanonična osnova v ℜ³

Družinski vektorji Yo, J in k Priznajo to isto zastopanje in za to so dovolj, da zastopajo vektorje v ℜ ³:

Yo =; J =;  k =

Pomeni, da se baza lahko izrazi na naslednji način:

B = ; ;

Da bi preverili, ali so linearno neodvisni, je determinanta, oblikovana z njimi, vektorji ne -nulski in tudi enaki 1:

Možno je tudi napisati kateri koli vektor, ki pripada ℜ ³ Kot linearna kombinacija le -teh. Na primer sila, katere pravokotne komponente so f_x = 4 n, f_in = -7 n in f_z= 0 N bi bilo zapisano v vektorski obliki, kot sledi:

F = N = 4Yo -7J + 0k N.

Zato Yo, J in k Make up ℜ sistem generatorja ³.

Druge ortonormalne baze v ℜ³

Standardna osnova, opisana v prejšnjem razdelku, ni edina ortonormalna baza v ℜ³. Tu imamo na primer baze:

B₁ = ; ;

B₂ = ; ;

Lahko je dokazano, da so te baze ortonormalne, saj se spomnimo pogojev, ki jih je treba izpolnjevati:

Vam lahko služi: valovita optika

-Vektorji, ki tvorijo osnovo, morajo biti pravokotni drug drugemu.

-Vsak od njih mora biti enoten.

Lahko ga preverimo, vedoč, da mora biti determinant, ki jo tvorijo.

Baza b₁ To je ravno pri cilindričnih koordinatah ρ, φ in z, še en način izražanja vektorjev v vesolju.

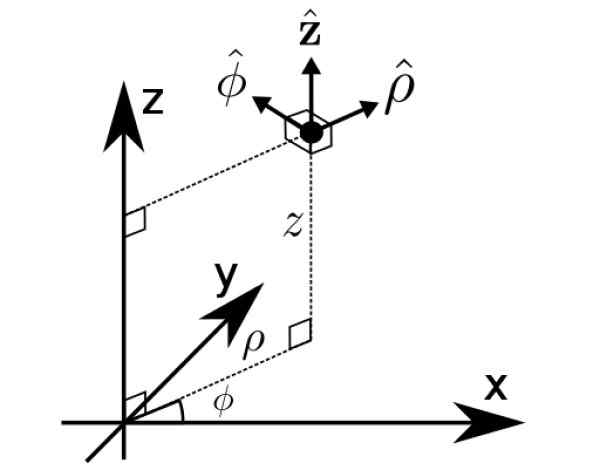Slika 2. Cilindrične koordinate. Vir: Wikimedia Commons. Math Buff [CC BY-S (https: // createCommons.Org/licence/by-sa/4.0)].

Rešene vaje

- Vaja 1

Pokažite, da je osnova b = ; ; je ortonormal.

Rešitev

Da bi pokazali, da so vektorji med seboj pravokotni, bomo uporabili skalarni izdelek, imenovan tudi notranja ali izdelka dveh vektorjev.

Pustite kakršna koli dva vektorja ali in v, Vaš skalarni izdelek je opredeljen z:

ali • v = ali.v. cosθ

Za razlikovanje vektorjev od njihovih modulov bomo uporabili krepko za prve in običajne črke za slednje. θ je kot med ali in v, Če so pravokotne, to pomeni, da je θ = 90 ° in skalarni izdelek ničen.

Če pa so vektorji podani v smislu njihovih komponent: ali = x, ali_in,ali_z > in v = x, v_in,v_z >, skalarni produkt obeh, ki je komutativen, se izračuna na ta način:

ali • v = ali_x .v_x + ali_in .v_in + ali_z .v_z

Na ta način so skalarni izdelki med vsakim parom vektorjev:

i) • = (3/5).(-4/5) + (4/5).((3/5) + 0.0 = (-12/25) + (12/25) = 0

Ii) • = 0

iii) • = 0

Za drugi pogoj se izračuna modul vsakega vektorja, ki ga dobimo z:

│u │ = √ (u_x² + ali_in² + ali_z²)

Tako so moduli vsakega vektorja:

│ = √ [(3/5)² + (4/5)²  + 0²) = √ [(9/25) + (16/25)] = √ (25/25) = 1

│ = √ [(-4/5)² + (3/5)²  + 0²) = √ [(16/25) + (9/25)] = √ (25/25) = 1

Lahko vam služi: drugo ravnotežno stanje: razlaga, primeri, vaje

│ = √ [0² + 0²  + 1²) = 1

Zato so trije vektorji enot. Končno določitev, ki jo tvorijo, ni nična in enaka 1:

- Vaja 2

Napišite vektorske koordinate W = V smislu prejšnje baze.

Rešitev

Za to se uporablja naslednji izrek:

Naj B = v₁, v₂, v₃,.. v_n Ortonormalna osnova v prostoru V z domačim izdelkom, vektorjem W Zastopa ga B na naslednji način:

W = <W•v₁> v₁ + <W•v₂> v₂ +<W•v₃> v₃ +.. <W•v_n> v_n

To pomeni, da lahko vektor napišemo na bazi B s koeficienti <W•v₁>, <W•v₂>, ..  <W•v_n>, za katero morate izračunati navedene skalarje:

• = (2).(3/5) + (3).(4/5) + 1.0 = (6/5) + (12/5) = 18/5

• = (2).(-4/5) + (3).(3/5) + 1.0 = (-8/5) + (9/5) = 1/5

• = 1

S pridobljenimi skalarnimi izdelki je zgrajena matrica, imenovana Koordinirana matrica od w.

Zato vektorske koordinate W V bazi B se izražajo skozi:

[W]_B= [(18/5); (1/5); 1]

Koordinatna matrika ni vektor, saj vektor ni enak njegovim koordinatam. To so le niz številk, ki služijo za izražanje vektorja v določeni bazi, ne pa vektor kot takega. Odvisni so tudi od izbrane baze.

Končno po teoremu vektor W bi bilo izraženo na naslednji način:

W = (18/5) v₁ + (1/5) v₂ + v₃

Z: v₁ =; v₂ =; v₃ =, To je osnovni vektorji B.

Reference

1. Larson, r. Osnove linearne algebre. 6. Izdaja. Cengage učenje.
2. Larson, r. 2006. Izračun. 7. Izdaja. Zvezek 2. McGraw Hill.
3. Salas, J. linearna algebra. Tema 10. Ortonormalne baze. Okreval od: OCW.UC3M.je.
4. Univerza Sevilla. Cilindrične koordinate. Vektorska baza. Okreval od: laplace.nas.je.
5. Wikipedija. Ortonormalna baza. Okrevano od: je.Wikipedija.org.