Konveksna definicija poligona, elementi, lastnosti, primeri

A Konveksni poligon Gre za geometrijsko figuro, ki jo vsebuje ravnina, ki je značilna, ker ima v notranjosti vse svoje diagonale in njeni koti merijo manj kot 180 °. Med njenimi lastnostmi so naslednje:

1) Sestavljen je iz N zaporednih segmentov, kjer se prvi segmenti pridruži prvemu. 2) Noben od segmentov ni prestopil tako, da ravnino omejuje v notranjost in drugo zunanjost. 3) Vsak koti notranjega območja je strogo nižji od ravnega kota.

Slika 1. Poligoni 1, 2 in 6 so konveksni. (Pripravil Ricardo Pérez).

Preprost način za ugotovitev, ali je poligon konveksn ali ne upošteva črte, ki poteka skozi eno od njegovih strani, ki določa dva semiplana. Če na vsaki vrstici, ki prehaja na eni strani, so druge strani poligona v istem semiplanu, je potem konveksni poligon.

[TOC]

Elementi poligona

Vsak poligon je sestavljen iz naslednjih elementov:

- Strani

- Točke

Strani so vsak od zaporednih segmentov, ki sestavljajo poligon. V poligonu noben od segmentov, ki ga sestavljajo.

Vrtice so sindikalne točke dveh zaporednih segmentov. V poligonu je število vrhov vedno enako številu strani.

Če dve strani ali segmenti poligonskega križa, potem imate križni poligon. Prehodna točka se ne šteje za točko. Križni poligon je nekonveksni poligon. Zrušini poligoni so prekrižani poligoni in zato niso konveksni.

Lahko vam služi: analitična geometrija

Ko ima poligon vse svoje stranice iste dolžine, potem obstaja navaden poligon. Vsi redni poligoni so konveksni. 

Konveksni in nekonveksni poligoni

Slika 1 prikazuje več poligonov, nekateri so konveksni, drugi. Analizirajmo jih:

Številka 1 je trikotni poligon (trikotnik) in vsi notranji koti so manjši od 180 °, zato je konveksni poligon. Vsi trikotniki so konveksni poligoni.

Številka 2 je štirikotni poligon (štirikolesni), kjer nobena od strani ni prestrežena in tudi vsaka notranja kota je manjša od 180 °. Nato je štiristranski konveksni poligon (konveksni štirikolesnik).

Po drugi strani je številka 3 štirinožni poligon, vendar je eden od njegovih notranjih kotov večji od 180 °, zato ne ustreza konveksnosti. To pomeni, da je nekonveksni poligon, ki se imenuje konkavni štirikotnik.

Številka 4 je poligon s štirimi segmenti (strani), od katerih sta dva prestrežena. Štirje notranji koti so manjši od 180 °, a ko dve strani prečkata, sta nekonveksna križni poligon (navzkrižni štirikolesnik).

Drug primer je številka 5. To je petstranski poligon, toda ker je eden od njegovih notranjih kotov večji od 180 °, je potem konkavni poligon.

Končno ima številka 6, ki ima tudi pet strani, vse svoje notranje kote manj kot 180 °, zato je petstranski konveksni poligon (konveksni pentagon).

Lahko vam služi: Napaka vzorčenja: formule in enačbe, izračun, primeri

Konveksne lastnosti poligona

1- Netrpani poligon ali preprost poligon razdeli ravnino, ki ga vsebuje v dve regiji. Notranja regija in zunanja regija, ki je poligon mejo med obema regijama.

Če pa je dodatno poligon konveksn, potem obstaja notranja regija, ki je preprosto povezana, kar pomeni, da ga jemljete dve točki notranje regije, vedno ga lahko združuje segment, ki spada v celotno notranjo regijo.

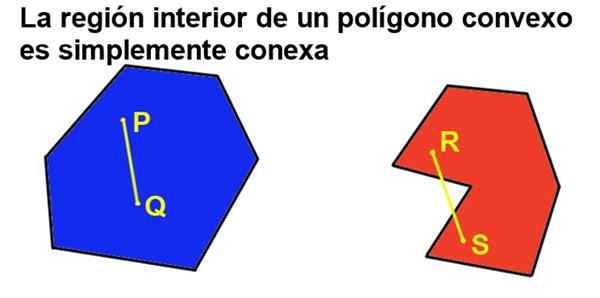Slika 2. Konveksni poligon je preprosto povezan, medtem ko konkave ni. (Pripravil Ricardo Pérez).

2- Ves notranji kot konveksnega poligona je manjši od ravnega kota (180 °).

3- Vse notranje točke konveksnega poligona vedno pripadajo enemu od pol definiranih s črto, ki poteka skozi dve zaporedni točki.

4- V konveksnem poligonu so vse diagonale v celoti vsebovane v notranjih poligonskih območjih.

5- Notranje točke konveksnega poligona pripadajo v celoti v konveksni kotni sektor, ki ga določa vsak notranji kot.

6- Vsak poligon, v katerem so vsi njeni točki na obodu, je konveksni poligon, ki se imenuje ciklični poligon.

7- Vsak ciklični poligon je konveksni, vendar ni vsak konveksni poligon cikličen.

8- Vsak, ki ni drobljen poligon (preprost poligon), ki ima vse njegove strani enake dolžine, je izbočen in je znan kot redni poligon.

Diagonale in koti v konveksnih poligonih

9- Skupno število diagonalov konveksnega poligona N strani je podano z naslednjo formulo:

Lahko vam služi: polibalna grafika

N = ½ n (n - 3)

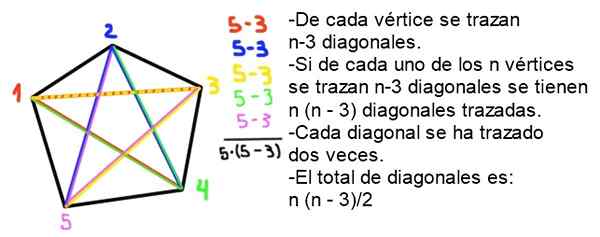
Demonstracija: V konveksnem poligonu N straneh vsakega vrha so narisani N - 3 diagonale, saj sta sama vrha in oba sosednja izključena. Ker je n vrhov, jih narišemo v skupno n - 2) diagonale, vendar je bila vsaka diagonala narisana dvakrat, tako da je število diagonalov (brez ponovitve) n (n -2)/2.

10- Vsota notranjih kotov konveksnega poligona N strani je podana z naslednjim razmerjem:

S = (n - 2) 180 °

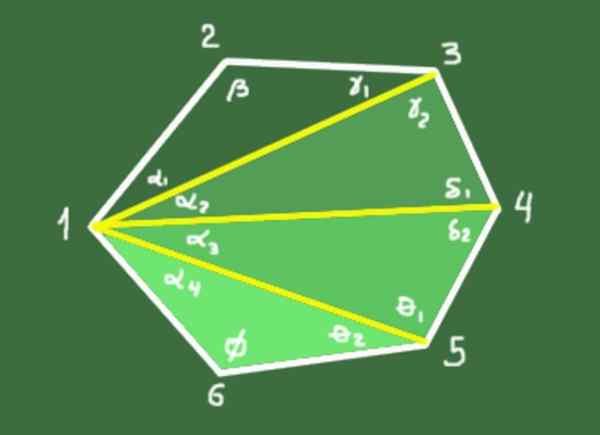
Demonstracija: Diagonale N-3 so črpane iz vrha, ki definirajo trikotnike N-2. Vsota notranjih kotov vsakega trikotnika je 180 °. Skupna vsota kotov N-2 trikotnikov je (N-2)*180 °, kar sovpada z vsoto notranjih kotov poligona.

Primeri

Primer 1

Ciklični šesterokotnik, to je šeststranski poligon in šest vrhov, vendar so vsi točki na istem obodu. Ves ciklični poligon je izbočen.

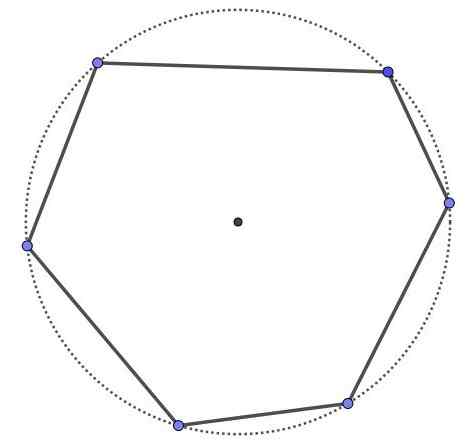Ciklični šesterokotnik.

Primer 2

Določite vrednost notranjih kotov običajnega Enegona.

Rešitev: Enegon je 9 -stranski poligon, hkrati pa ureja tudi vse njegove strani in koti so enaki.

Vsota vseh notranjih kotov 9 -stranskega poligona je:

S = (9 - 2) 180º = 7 * 180 ° = 1260 ° 

Vendar obstaja 9 notranjih kotov enakega merila α, zato je treba izpolniti naslednjo enakost:

S = 9 α = 1260 °

Od kod izhaja, da je merilo α vsakega notranjega kota običajnega Enegona:

α = 1260 °/9 = 140 °