Homocedičnost, kar je, pomen in primeri

The Homocedičnost V prediktivnem statističnem modelu se pojavi, če je v vseh podatkovnih skupinah enega ali več opazovanj odstopanje modela glede na razlagalne (ali neodvisne) spremenljivke ostane konstantno.

Regresijski model je mogoče homocedastičen ali ne, v tem primeru govorimo heterocedicity.

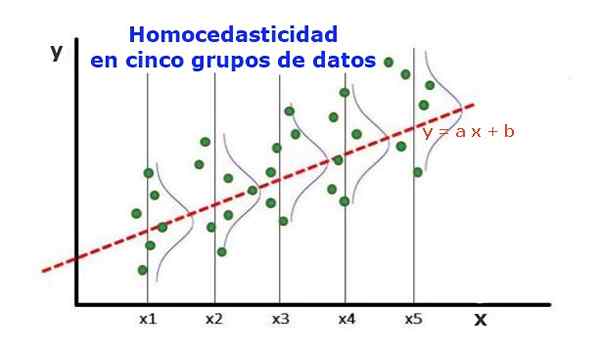
Slika 1. Pet podatkovnih skupin in regresijska prilagoditev niza. Varianta glede predvidene vrednosti je enaka v vsaki skupini. (UPAV-LIBRARY.org)

Statistični regresijski model več neodvisnih spremenljivk se imenuje homocedastično, le če varianta predvidene spremenljive napake (ali standardni odklon odvisne spremenljivke) ostane enakomerna za različne skupine razlagalnih ali neodvisnih spremenljivk.

V petih podatkovnih skupinah na sliki 1 je bila varianca izračunana v vsaki skupini glede na vrednost, ki jo ocenjuje regresija, in je v vsaki skupini postala enaka. Domneva se tudi, da podatki sledijo običajni porazdelitvi.

Na grafični ravni pomeni, da so točke enako razpršene ali razpršene okoli predvidene vrednosti z regresijsko prilagoditvijo in da ima regresijski model enako napako in veljavnost za obseg pojasnjevalne spremenljivke.

[TOC]

Pomen homocedičnosti

Za ponazoritev pomena homocedastičnosti v napovedni statistiki je treba v nasprotju z nasprotnim pojavom, heterocedičnostjo.

Homocedastičnost v primerjavi s heterocedičnostjo

V primeru slike 1, v kateri je homocedičnost, je izpolnjeno:

Var ((y1-y1); x1) ≈ var ((y2-y2); x2) ≈ ... var (y4-y4); x4)

Kjer var ((yi-ii); xi) predstavlja varianco, par (xi, yi) predstavlja dejstvo skupine I, Yi pa vrednost, ki napoveduje regresijo povprečne vrednosti XI skupine. Varianta podatkov skupine I se izračuna na naslednji način:

Var ((yi -ii); xi) = ∑j (yij - yi)^2/n

Nasprotno, ko pride do heterocedičnosti, regresijski model morda ne bo veljaven za celotno regijo, v katerem je bila izračunana. Slika 2 prikazuje primer te situacije.

Vam lahko služi: kaj so notranji nadomestni koti? (Z vajami)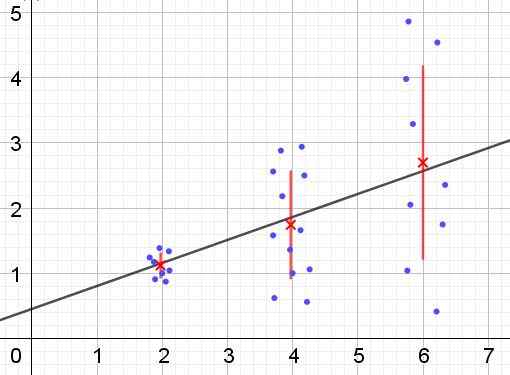 Slika 2. Podatkovna skupina, ki ima heterocedičnost. (Lastna izdelava)

Na sliki 2 so tri podatkovne skupine in niz nabora predstavljene z linearno regresijo. Treba je opozoriti, da so podatki v drugi in v tretji skupini bolj raztreseni kot v prvi skupini. Graf slike 2 prikazuje tudi povprečno vrednost vsake skupine in njegovo vrstico napak ± σ, ki je σ standardni odklon vsake podatkovne skupine. Ne pozabite, da je standardni odklon σ kvadratni koren variance.

Jasno je, da se v primeru heterocedicičnosti napaka regresijske ocene spreminja v območju vrednosti razlagalne ali neodvisne spremenljivke, v intervalih se ne uporablja.

V regresijskem modelu je treba napake ali odpadke (y -y) distribuirati z enako varianco (σ^2) v celotnem intervalu neodvisnih spremenljivih vrednosti. Zaradi tega mora dober regresijski model (linearni ali nelinearni) opraviti test homocedastičnosti. 

Preskusi homocedičnosti

Točke, prikazane na sliki 3, ustrezajo podatkom študije, ki išče razmerje med cenami (v dolarjih) hiš, odvisno od velikosti ali površine v kvadratnih metrih.

Prvi model, ki je vajen, je linearna regresija. Na prvem mestu je ugotovljeno, da je koeficient določitve r^2 prilagoditve precej visok (91%), zato je mogoče misliti, da je prilagoditev zadovoljiva.

Vendar pa lahko dve regiji jasno ločimo od grafa nastavitve. Eden od njih, tisti na desni, zaklenjen v ovalu, se srečuje s homocedastičnostjo, medtem ko območje levice nima homocedastičnosti.

Vam lahko služi: ocena polinoma: kako je določena, primeri in vaje

To pomeni, da je napoved regresijskega modela ustrezna in zanesljiva v razponu med 1800 m^2 do 4800 m^2, vendar zelo neprimerna zunaj te regije. Na heterocedičnem območju ni samo napaka zelo velika, ampak tudi podatki sledijo drugemu trendu, ki se razlikuje od predlaganega modela linearne regresije.

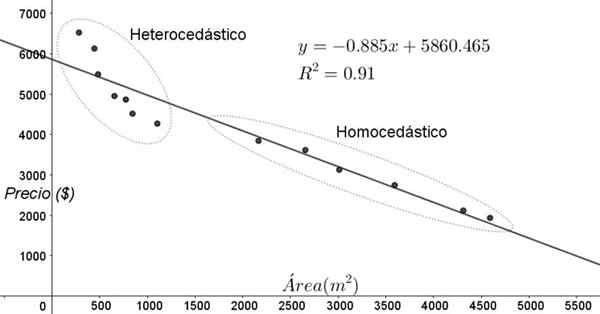Slika 3. Cene stanovanj v primerjavi z območjem in napovednim modelom z linearno regresijo, ki kažejo na območja homocedastičnosti in heterocedičnosti. (Lastna izdelava)

Graf disperzije podatkov je najpreprostejši in najbolj vizualni test njihove homocedastičnosti, vendar včasih ni tako razviden, kot je prikazan na sliki 3, se je treba zateči k grafiki s pomožnimi spremenljivkami.

Standardizirane spremenljivke

Z namenom ločitve območij, na katerih je izpolnjena homocedastičnost in v katerih ne, se uvedejo standardizirane spremenljivke ZRES in ZDEDED:

Zres = abs (y - y)/σ

Zpred = y/σ

Treba je opozoriti, da so te spremenljivke odvisne od uporabljenega regresijskega modela, saj gre za vrednost regresijske napovedi. Spodaj je Graf z disperzijo ZRES vs za isti primer:

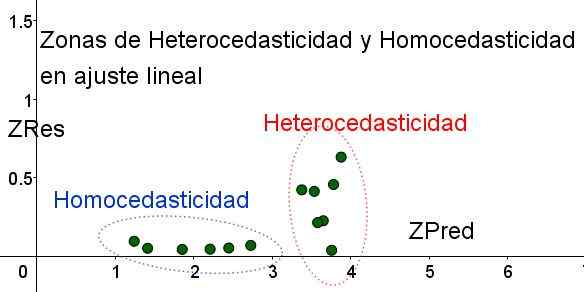Slika 4. Treba je opozoriti, da v območju homocedastičnosti ZRES ostane enoten in majhen v območju napovedovanja (lastna obdelava).

Na grafu slike 4 s standardiziranimi spremenljivkami je območje, kjer je preostala napaka majhna in enakomerna, jasno ločena, glede na tisto, ki ne. Na prvem območju je homocedastičnost izpolnjena, medtem ko je preostala napaka zelo spremenljiva in velika.

Regresijska prilagoditev se uporablja za isto podatkovno skupino 3. Rezultat je prikazan na naslednji sliki:

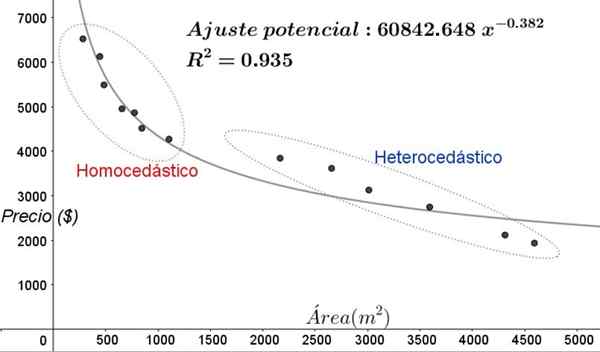Slika 5. Nova območja homocedastičnosti in heterocedicisti v prilagajanju podatkov z nelinealnim regresijskim modelom. (Lastna izdelava).

Na grafu slike 5 je treba jasno opaziti homocedična in heterocedikastična območja. Prav tako je treba opozoriti, da so bila ta območja izmenjana glede na tiste, ki so bila oblikovana v modelu linearne prilagoditve.

Vam lahko služi: vrste kotov, značilnosti in primerov

Na grafu slike 5 je razvidno, da tudi kadar je koeficient določanja prilagoditve precej visok (93,5%), model ni primeren za celoten interval pojasnjevalne spremenljivke, saj podatki za vrednosti, starejše od leta 2000 m^2 ima heterocedastičnost.

Neegrafski testi homocedastičnosti

Eden najbolj uporabljenih ne -grafičnih testov za preverjanje, ali je izpolnjena homocedastičnost ali ne, je Breusch-poganski test.

Vse podrobnosti tega testa ne bodo podane v tem članku, vendar so njegove temeljne značilnosti in iste korake široko opisane:

1. Regresijski model se uporablja za podatke N, varianta istega pa se izračuna glede na vrednost, ki jo oceni model σ^2 = ∑j (yj - y)^2/n.
2. Določena je nova spremenljivka ε = ((yj - y)^2) / (σ^2)
3. Za novo spremenljivko se uporablja isti regresijski model in izračunajo se njeni novi regresijski parametri.
4. Določena je kritična vrednost Chi kvadrata (χ^2), kar je polovica vsote kvadratov novih odpadkov v spremenljivki ε.
5. Tabela za distribucijo kvadrata CHI se uporablja glede na stopnjo pomembnosti na osi x (običajno 5%) in število stopenj svobode (#OF regresijske spremenljivke, razen enote), da dobimo vrednost plošče.
6. Kritična vrednost, dobljena v koraku 3, primerjamo z vrednostjo, ki jo najdemo v tabeli (χ^2).
7. Če je kritična vrednost nižja od tabele, imate ničelno hipotezo: obstaja homocedičnost
8. Če je kritična vrednost nad vrednostjo tabele, imate alternativno hipotezo: ni homocedastičnosti.

Večina statističnih računalniških paketov, kot so: SPSS, Minitab, R, Python Pandas, SAS, Statgraphic in več drugih vključuje test homocedastičnosti Breusch-poganski. Še en test za preverjanje enakomernosti variance Levene test.

Reference

1. Box, Hunter & Hunter. (1988) Statistika za raziskovalce. Obrnil sem urednike.
2. Johnston, J (1989). Metode ekonometrije, urednikov Vicens -ves.
3. Murillo in González (2000). Priročnik za ekonometrijo. Univerza v Las Palmas de Gran Canaria. Pridobljeno iz: ULPGC.je.
4. Wikipedija. Homocedičnost. Okrevano od: je.Wikipedija.com
5. Wikipedija. Homoscedastičnost. Pridobljeno iz: v.Wikipedija.com