Trigonometrični razlogi Primeri, vaje in aplikacije

The Trigonometrični razlogi So količniki ali razlogi, ki jih je mogoče storiti z vrednostjo strani pravega trikotnika. Te strani so: dve kategoriji, ki tvorita 90 ° drug drugega in hipotenuza, ki tvori akutni kot θ z eno od kategorij.

6 količnikov je mogoče oblikovati. Njihova imena in ustrezne okrajšave so:

• Čast (sen)
• Coseno (cos)
• tangenta (TG ali TAN)
• Cotangent (CTG ali Cotan)
• Secante (sec) in
• kombajn (harmonija)

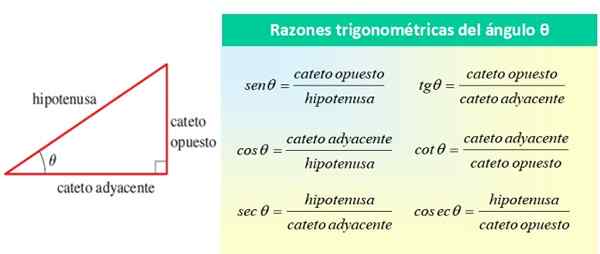
Vsi so se sklicevali na kot θ, kot je prikazano na naslednji sliki:

Slika 1. Trigonometrični razlogi akutnega kota θ. Vir: f. Zapata.

Osnovni trigonometrični razlogi kota θ so sin θ, cos θ in tan θ, preostale razloge pa se lahko izrazijo v smislu teh treh. Iz prejšnje slike si to lahko ogledate:

• Sec θ = 1/ cos θ
• Škoda θ = 1/ sin θ
• COT θ = 1/tg θ

Velikost strani trikotnika ne vpliva na vrednost razlogov, saj sta dva trikotnika, katerih koti merijo isto.

[TOC]

Primer

Na primer, izračunajmo trigonometrične razloge kot θ v naslednjih trikotnikih:

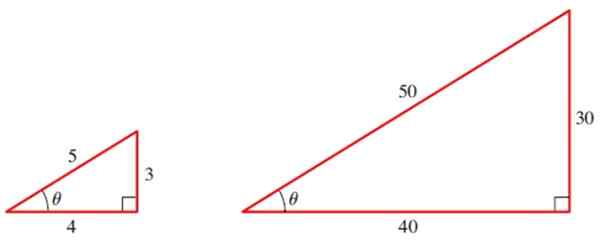Slika 2. Dva podobna trikotnika imata enake trigonometrične razloge za svoje kote. Vir: Stewart, J.Predhodno: matematika za izračun.

Za majhen trikotnik imamo tri osnovne razloge kot θ:

sin θ = 3/5

cos θ = 4/5

tg θ = ¾

In zdaj izračunamo tri osnovne razloge θ z velikim trikotnikom:

sin θ = 30/50 = 3/5

cos θ = 40/50 = 4/5

Tg θ = 30/40 = ¾

Pomembna podrobnost je treba upoštevati: tako sin θ in cos θ sta manjša od 1, saj kategorije vedno merijo manj kot hipotenuza. Prav zares:

sin θ = 3/5 = 0.6

cos θ = 4/5 = 0.8

Rešene vaje

V naslednjih vajah je treba rešiti pravi trikotnik, kar pomeni najti dolžino treh strani in merilo notranjega kota, od katerih eden vedno meri 90 °.

Lahko vam služi: Prvo -stopinjska enačbe: formula, kako jih rešiti, primer, vaje

Teorem Pythagora velja za pravokotnike in je zelo koristen, kadar sta znani dve strani in manjkajo, da je treba določiti. Teorem pravi:

Hipotenuse² = nasproti Cateto² + sosednji cateto²

Teorem pitagore lahko preverimo z majhnim trikotnikom slike 2, katerega noge so 3 in 4. Vrstni red, v katerem se sprejmejo kategorije. Uporaba teorema imamo:

Hipotenuse² = 3² + 4² = 9 + 16 = 25

Zato je hipotenuza:

Hipotenuse = √25 = 5

- Vaja 1

Izračunajte trigonometrične razloge kotov, prikazanih v naslednjih trikotnikih:

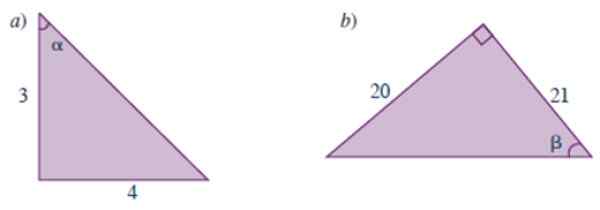Slika 3.- Trikotniki za leto so rešili 1. Vir: Carena, m. 2019. Priročnik za matematiko prednavdljivosti.

Rešitev

Ta trikotnik je enak na sliki 3, vendar nas prosijo za trigonometrične razloge drugega akutnega kota, označene z α. Izjava ne ponuja vrednosti hipotenusa z uporabo teorema Pitagore, ki vemo, da je vredno 5.

Razlogi je mogoče izračunati neposredno iz definicije, pri izbiri noge, ki je nasprotno od kota α. Pa poglejmo:

• sin α = 4/5
• cos α = 3/5
• Tg α = 4/3
• COT α = ¾
• Sec α = 1/(3/5) = 5/3
• Škoda α = 1/(4/5) = 5/4

In kot vidimo, so bile izmenjane vrednosti trigonometričnih razlogov. Dejansko sta α in θ dopolnilna kota, kar pomeni, da dodata 90 °. V tem primeru je izpolnjeno, da je Sen α = cos θ in tako naprej iz drugih razlogov.

Rešitev b

Izračunamo hipotenuzo trikotnika skozi izrek pitagore:

Hipotenuse² = 20² + enaindvajset² = 841

√841 = 29

Potem so 6 trigonometričnih razlogov kota β:

• Sen β = 20/29
• cos β = 21/29
• TG β = 20/21
• COT β = 21/20
• Sec β = 1/(21/29) = 29/21
• Škoda β = 1/(20/29) = 20/29

Vam lahko služi: kombinirane operacije

- Vaja 2

a) Poiščite vrednost x na sliki.

b) Izračunajte obod prikazanih 3 trikotnikov.

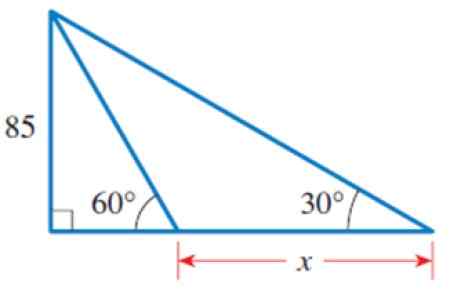Slika 4. Trikotniki za leto razrešijo 2. Vir: Stewart, J. Predhodno: matematika za izračun.

Rešitev

Na sliki lahko identificiramo več trikotnikov, zlasti trikotnik pravokotnika levice, ki ima kategorijo, ki je enaka 85 in akutni kot 60 °.

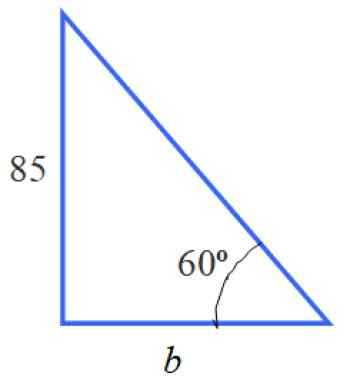Slika 5. Trikotnik na levi.

Z informacijami tega trikotnika lahko izračunamo stran B. Izjava ne zahteva ukrepa, ampak poznavanje njene vrednosti je prejšnji korak.

Za določitev ustreznega razloga je tg 60 ° = 85 /b, saj je B noga, ki meji na 60 ° in 85 nasprotno omenjenemu kotu. Zato:

B = 85 / tg 60º = 85 / √3

Ko bomo poznali B, bomo uporabili velik in zunanji pravokotnik, ki ima skupno stran s prejšnjim trikotnikom: tisti, ki meri 85. To je kateto, ki nasprotuje kot 30 °.

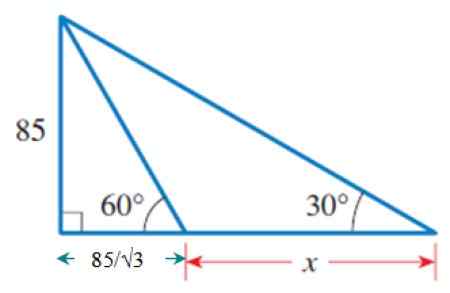Slika 6. Zunanji trikotnik, katerega del baze je že znan.

Od tod:

Cateto, ki meji na 30 ° = (85/√3) + x

Zdaj lahko dvignemo naslednje:

85 / [(85 / √3) + x] = tg 30 °

Kaj je v kvadratnih oklepajih, pomnožite 30 ° TG:

85 = [(85/√3) + x]. TG 30 °

Uporaba distribucijske lastnosti množenja:

85 = tg 30 °. (85/√3) + x. TG 30 °

Zato:

x.TG 30 ° = 85 - TG 30 °. (85/√3) = 85 [1 - TG 30 ° . (1/√3)] = 85 . (2/3) = 170/3

Zamenjava vrednosti TG 30 ° = √3 / 3:

x = (170/3) ÷ (√3 / 3) = 98.petnajst

Rešitev b

Obod majhnega trikotnika

Biti h₁ Hipotenuza tega trikotnika, ki jo lahko izračunamo s teorem pitagore ali s trigonometričnim razlogom, na primer COS 60 °:

cos 60 ° = 85 / √3 / h₁→ H₁ = (85/√3) ÷ cos 60º = 98.1

Če želite najti P, obod tega trikotnika, preprosto dodamo 3 strani:

Vam lahko služi: opisna statistika: zgodovina, značilnosti, primeri, koncepti

P = 85 + (85/√3) + 98.1 = 232.2

Obod zunanjega trikotnika

Biti h₂ na hipotenuzo zunanjega trikotnika:

Sen 30 ° = 85 ÷ h₂  

h₂ = 85 ÷ greh 30 ° = 170

Za ta trikotnik je obod:

P = 85 + [(85/√3) + 98.15] + 170 = 402.22

Obod trikotnika, ki ne

Iz tega trikotnika že poznamo vse njegove strani:

P = x + h₁ + h₂ = 98.15 + 98.15 + 170 = 366.3

Aplikacije trigonometričnih razlogov

Trigonometrični razlogi imajo številne praktične aplikacije, na primer višine je mogoče izračunati.

Recimo, da je vodni stolp od stavbe 325 čevljev. Opazovalec, ki se nahaja v oknu, zapiše, da je višinski kot zgornjega konca stolpa 39 °, medtem ko je kot depresije, s katerim se vidi podstavek stolpa, 25 °. Čudeži:

a) Kakšna je višina stolpa?

b) koliko je okno?

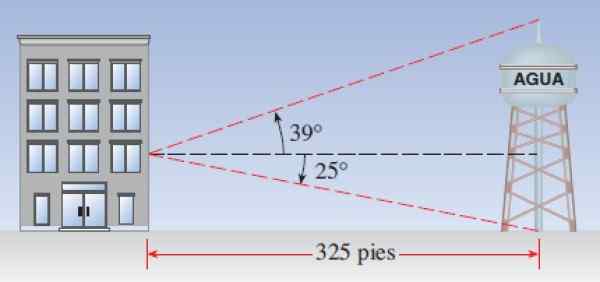Slika 7. Shema za izračun višine Vista Torre iz stavbe. Vir: Stewart, J. Predhodno: matematika za izračun.

Rešitev

Od kateta nasproti do 39 zgornjega trikotnika dobimo del odgovora:

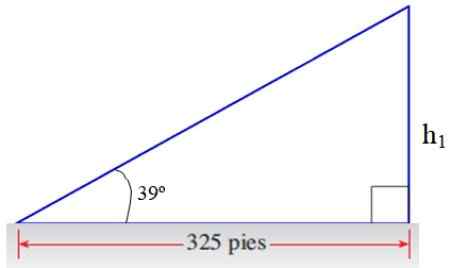Slika 8. Trikotnik za vadbo aplikacije. Vir: f. Zapata.

h₁/325 = TG 39º → H₁ = 325 . TG 39 ° FEET = 263.2 stopala

Na podoben način dobimo preostanek višine stolpa, imenovan H₂ Od spodnjega trikotnika:

h₂/325 = TG 25 ° → H₂ = 325 . Tg 25 ° čevlje = 151.6 čevljev

Skupna višina stolpa je h₁ + h₂ = 263.2 + 151.6 čevljev = 414.7 čevljev.

Rešitev b

Okno je natančno na višini h₂ tla:

h₂ = 151.6 čevljev.

Reference

1. Carena, m. 2019. Priročnik za matematiko prednavdljivosti. Nacionalna univerza na obali.
2. Hoffman, J. Izbira vprašanj matematike. Zvezek 3.
3. Jiménez, r. 2008. Algebra. Dvorana Prentice.
4. Stewart, J. 2006. Predhodno: matematika za izračun. 5. Izdaja. Cengage učenje.
5. Zill, d. 1984. Algebra in trigonometrija. McGraw Hill.