Kaj so trikotne številke? Lastnosti in demonstracije

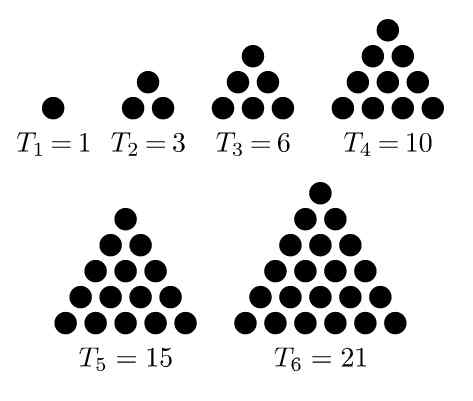
Znano je kot Trikotne številke do zaporedja števil, ki jih dobimo z ureditvijo ali figuro točk enakostraničnega trikotnika. Prva od zaporedja so: 1, 3, 6, 10, 15, 21, ..

Prva trikotna številka je 1, drugo je 3, saj je pridobljen z dodajanjem dvotesne vrstice v prejšnjo, da tvori enakostranični trikotnik treh elementov.

Slika 1. Zaporedje prvih šestih trikotnih številk. Vir: Wikimedia Commons. Melchoir/cc by-sa (https: // creativeCommons.Org/licence/by-sa/3.0

Tretji je 6, ki se pojavi pri dodajanju tri točke vrstice prejšnjemu dogovoru, tako da se na strani oblikuje tri -točkovni trikotnik. 10 zaporedja dobimo z dodajanjem druge vrstice prejšnji razporedi.

Formula, ki vam omogoča iskanje elementa n Iz trikotnega zaporedja je znana sprednja trikotna številka:

T_n = T_N-1 + n

Seznam prvih šestih trikotnih števil je dosežen takole:

-Najprej: 1

-Drugi: 1 + 2 = 3

-Tretjič: (1 +2) + 3 = 3 + 3 = 6

-Soba: (1 + 2 + 3) + 4 = 6 + 4 = 10

-Peti: (1 + 2 + 3 + 4) + 5 = 10 + 5 = 15

-Šesti: (1 + 2 + 3 + 4 + 5) + 6 = 15 + 6 = 21

[TOC]

Lastnosti trikotnih številk

1.- N-Simo TN Trikotno število zaporedja trikotnih številk je polovica N, pomnožena z n+1:

T_n = ½ n (n+1)

2.- Vsota trikotne številke n-Ésimo s sprednjo trikotno številko, torej (n-1) -heimo, je kvadratno povišana:

T_n + T_N-1= n²

3.- Razlika v trikotni številki n-to je manj trikotna n-Ésimo manj ena je n:

T_n - T_N-1 = n

4.- Vsota prvih trikotnih števil se imenuje tetraedrska številka Sn in je enaka šestemu delu izdelka, pomnoženega z (n + 1) in pomnoženo z (n + 2):

Vam lahko služi: obdavčitev

S_n= ⅙ n (n + 1) (n + 2)

5.- Vsako naravno število n je rezultat vsote treh trikotnih števil:

N = Δ1 + Δ1 + Δ3

To zadnjo nepremičnino ali izrek je odkril veliki matematik Carl Friedrich Gauss leta 1796, ki ga je v svojem dnevniku dosegel tako, da je postavil grško občudovanje Eureka! kaj to pomeni "To sem dosegel".

To je bila ista beseda, ki jo je veliko prej uporabljal grški Arhimedi, ko je določil navidezno težo potopljenega telesa.

V tem razmerju je ničelna številka vzeta kot trikotno in lahko pride do ponovitve.

Demonstracije

- Demonstracija 1

Dokažite, da trikotna številka n-To je:

T_n = ½ n (n+1)

Prejšnjo formulo je enostavno sklepati, če se zavedamo, da lahko trikotni razporeditvi dodamo enako število točk, da tvorimo štirikolesnik točk.

Ker je skupno število ureditvenih točk v obliki štirikotnika, je število vrstic n pomnoženo s številom stolpcev (N+1), Potem bo imel trikotna ureditev le polovico točk ureditve v obliki štirikotnika.

Tu je prikazano na sliki 2.

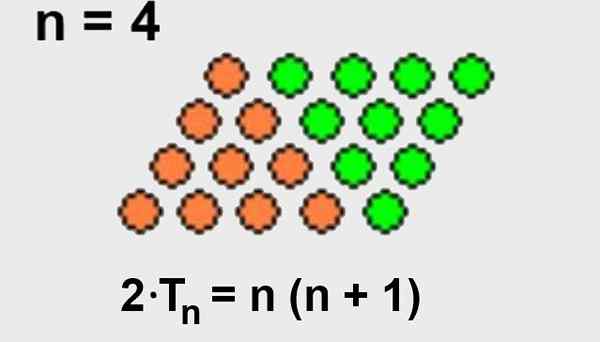Slika 2. Square -oblikovana razporeditev, v kateri je skupno število točk število vrstic n, pomnožene s številom stolpcev n+1. Skupno število točk je tudi dvakrat več kot trikotne ureditve. Vir: Wikimedia Commons.

- Demonstracija 2

Dokazujejo, da vsota n-To trikotno številko z n-Manj ena Trikotno število je n na kvadrat:

T_n + T_N-1= n²

Že se je pokazalo, da trikotno število n-To daje:

T_n= ½ n (n+1)

Zato je sprednja trikotna številka:

T_N-1 = ½ (n-1) ((n-1) + 1) = ½ n (n-1)

Vsota obeh ostaja:

T_n + T_N-1 = ½ n (n + 1) + ½ n (n - 1)

½ N se vzame za pridobitev:

T_n + T_N-1 = ½ n [(n + 1) + (n - 1) = ½ n [n + 1 + n - 1]

In takoj je izraz poenostavljen znotraj nosilca:

Lahko vam služi: ocena po presledkih

T_n + T_N-1 = ½ n [2 n] = ½ 2 n ⋅ n

Zdaj pa se spomnite, da je ½ za 2 1 in da je n za n kvadrat, imate:

T_n + T_N-1 = n²

Ta lastnost je lahko tudi geometrična, trikotnik je preprosto dokončan tako, da tvori kvadrat, kot je prikazano na sliki 3.

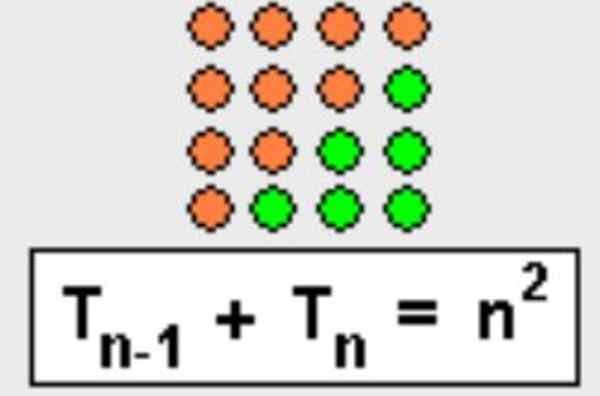Slika 3. Vsota trikotne številke N-Ésimo s sprednjo trikotno številko je enaka N kvadratu. Vir: Wikimedia Commons.

- Demonstracija 3

Razlika v trikotnem številu reda n minus trikotno število reda N-1 je n:

T_n - T_N-1 = n

To je mogoče preizkusiti preprosto tako, da se spomnimo, da je naslednje trikotno število pridobljeno iz prejšnje skozi formulo:

T_n = T_N-1 + n

In od tam je očitno, da T_n - T_N-1 = n. Prav tako ga je enostavno grafično vizualizirati, kot je prikazano na sliki 4.

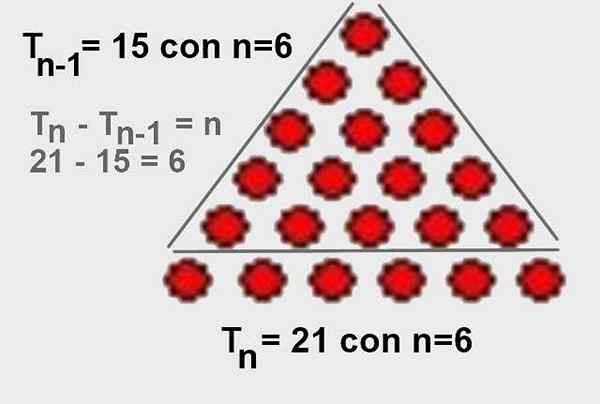Slika 4. Razlika trikotnega števila reda n manj. Vir: Wikimedia Commons.

- Demonstracija 5

Vsota prvih trikotnih n številkn Je enak šestemu delu izdelka, pomnoženega z (n + 1) in pomnoženo z (n + 2):

S_n = ⅙ n (n + 1) (n + 2)

Uporabimo trikotno število vrstnega reda n: T_n= ½ n (n+1). Vsota prvega n Trikotne številke bodo označevale za S_n  

Na primer, S₁ pomeni vsoto prvega trikotnega vprašanja, ki bo nedvomno 1.

Potem pa poglejmo, ali je formula, ki jo poskusimo poskusiti, izpolnjena z n = 1:

S₁ = ⅙ 1⋅2⋅3 = 1

Dejansko je formula za n = 1 preverjena. Enostavno je vizualizirati, da bo vsota N+1 prvih trikotnih številk vsota prvega n več naslednje trikotne številke:

S_N+1 = S_n + T_N+1

Zdaj predpostavimo formulo S_n Izpolnjena je za n, nato pa ga zamenjamo v prejšnjem izrazu in dodamo trikotno število vrstnega reda N+1:

S_N+1 = [⅙ n (n + 1) (n + 2)] + [½ (n + 1) (n + 2)]]

Vam lahko služi: pravokotna črta: značilnosti, primeri, vaje

Poglejmo korak za korakom, kaj je pridobljeno:

-Izvajamo vsoto obeh frakcijskih izrazov:

S_N+1 = [2 n (n + 1) (n + 2) + 6 (n + 1) (n + 2)] /12 

-Odstranjen je iz števca, ki je skupni na 2 (n + 1) (n + 2) in poenostavi:

S_N+1 = 2 (n + 1) (n + 2) [n +3] / 12 = (n + 1) (n + 2) (n +3) / 6

Prejšnji rezultat se strinja s formulo Sn Če je N+1 zamenjan, kar je bilo dokazano z indukcijo formula vsote prvih trikotnih izrazov.

Tetraedrska številka

Rezultat se imenuje Tetraedrska številka reda n, Ker je kot nabiranje trikotnih plasti, ki tvorijo tetraeder, kot je prikazano v naslednji animaciji.

Slika 5. Vsota N trikotnih številk ustreza kup plasti N, N-1, ..., 1 trikotnikov, ki tvorijo navaden tetraedron. Vir: Wikimedia Commons.

Reference

1. Camacho J. Nepričakovan videz trikotnih številk. Okrevano od: Masscience.com
2. Claudio. Trikotne številke. Obnovljeno od: preprosto številke. Blogspot. com
3. Wikipedija. Trikotna številka. Okrevano od: je.Wikipedija.com
4. Wikipedija. Trikotna številka. Pridobljeno iz: v.Wikipedija.com
5. Wikipedija. Številka Tretraedra. Pridobljeno iz: v.Wikipedija.com