Statični koeficient trenja, primer, vaja

The statično trenje To je sila, ki nastane med dvema površinama, ko ena površina ne drsi glede na drugo. Zelo pomembno je, saj nam omogoča napredovanje pri hoji, saj je sedanja sila med tlemi in podplatom čevljev. 

Tudi statično trenje se pojavlja med pnevmatikami pločnikov in avtomobilskih pnevmatik. Če ta sila ni prisotna, se avtomobil ne more začeti premikati, kot v avtomobilu, ki poskuša začeti na ledeni površini: kolesa drsi, vendar avtomobil ne napreduje.

Slika 1. Ilustracija o trenju

Statično trenje je odvisno od hrapavosti površin v stiku in tudi od vrste materiala. Zato so pnevmatike in športni čevlji gume, da bi povečali trenje s pločnikom.

V modelu statičnega trenja sta značilnosti materiala in stopnja hrapavosti med površinami povzeti v številu, imenovanem Statični koeficient trenja, ki je določena eksperimentalno.

[TOC]

Statični koeficient trenja

Slika 2. Knjiga na nagnjeni tabeli ostaja v mirovanju zaradi statične sile trenja med knjigo in mizo. Vir: f. Zapata.

Zgornja slika prikazuje knjigo, ki je v mizi, ki ima naklon 15,7 °.

Če bi bile površine knjige in mize zelo gladke in polirane, knjige ni bilo mogoče hraniti v mirovanju. Ker pa niso, se zdi sila, ki je tangentna na površine v stiku, imenovana sila statično trenje. 

Če je bil naklonski kot dovolj velik, potem ni dovolj statično trenje Za uravnoteženje knjige in to bi začelo drseti.

V tem primeru obstaja tudi trenje med knjigo in mizo, vendar bi bilo to sila Dinamično trenje, tudi poklican Kinetično trenje.

Obstaja meja med statičnim trenjem in dinamičnim trenjem, ki se pojavi za trenutek, ko statično trenje doseže največjo vrednost.

Vam lahko služi: Dopplerjev učinek: opis, formule, primeri, primeri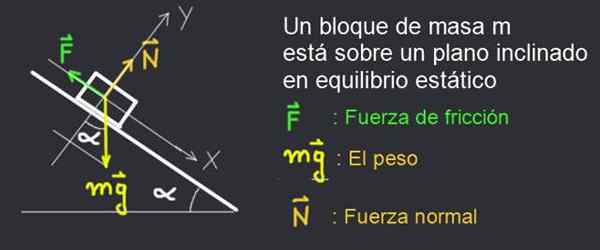Slika 3. Blok počitka na nagnjeni ravnini je v mirovanju zaradi statične sile trenja. Vir: f. Zapata.

Razmislite na sliki 2, diagram sile knjige mase m, ki ostane v mirovanju na α naklonski ravnini.

Knjiga ostaja v mirovanju, ker sil trenja F, statična vrsta, uravnoteži sistem.

Če kot naklon nekoliko raste, morajo kontaktne površine oskrbovati več trenja, vendar količino statičnega drgnjenja_Max, to pomeni:

F ≤ f_Max.

Najvišja statična sila bo odvisna od materialov in stopnje hrapavosti površin v stiku, pa tudi od trdnosti oprijema.

Statični koeficient trenja μ_in To je pozitivno število, ki je odvisno od značilnosti površin v stiku. Normalna sila N da ravnina izvaja na bloku, je stopnja zategovanja med površino bloka in ravnino. Tako določijo največjo silo trenja, ki jo zagotavljajo površine, kadar ni zemeljskega plazu:

F_Max = μ_in N

Skratka, statična sila trenja sledi naslednjemu modelu:

F ≤ μ_in N

Primer: Določitev koeficienta statičnega trenja

Statični koeficient drgnjenja je brezdimenzionalno število, ki se eksperimentalno določi za vsak par površin. 

Blok upoštevamo na preostalem delu slike 2. Naslednje sile delujejo na njem:

- Trenje: F

- Teža masnega bloka m: mg

- Običajna sila: N

Ker je blok v mirovanju in nima pospeševanja, po Newtonovem drugem zakonu izhajajoča sila -a vektorska vsota -is praznina:

F + N + mg = 0

Velja za fiksni koordinatni sistem XY z osi x vzdolž nagnjene ravnine in osi ter pravokotno nanjo, kot je prikazano na sliki 2.

Lahko vam služi: Slišite silo: površinske in masne sile

Sile morajo biti ločene glede na njihove kartezijanske komponente, kar povzroča naslednji sistem enačb:

-Komponenta x: -F + mg sen (α) = 0

-Komponenta in: N - mg cos (α) = 0

Iz prve enačbe se razčisti vrednost statičnega trenja:

F = mg sen (α)

In druge vrednosti normalne sile:

N = mg cos (α)

Statična sila trenja je posledica naslednjega modela:

F ≤ μ_in N

Zamenjava neenakosti prej dobljene vrednosti imamo:

mg sen (α) ≤ μ_in mg cos (α)

Upoštevamo, da so za vrednosti α med 0 ° in 90 ° funkcije sinusa in kosinusa pozitivne in da je količnik med dojko in kosinusom tangent, smo zapustili:

Tan (α) ≤ μ_in

Enakost je izpolnjena za določeno vrednost α, ki se imenuje kritični kot in da označujemo za α*, torej:

μ_in = Tan (α*)

Kritični kot se določi eksperimentalno in postopoma povečuje naklon na pravi kot, v katerem blok začne drseti, to je kritični kot α*.

V knjigi na sliki 1 je bil ta kot določen eksperimentalno, kar je povzročilo 24 °. Potem je koeficient statičnega trenja:

μ_in = Tan (24 °) = 0,45.

To je pozitivno število med 0 in neskončnostjo. Da μ_in = 0 površin so popolnoma gladke. Da μ_in → ∞ Površine so popolnoma povezane ali varjene.

Običajno je vrednost koeficienta trenja med 0 in 10.

Vaja

Na dirkah Pique ali dragsters se med začetkom dosežejo pospeški do 4G, ki jih dosežemo natančno, kadar pnevmatike ne drsijo glede na pločnik.

To je zato, ker je koeficient statičnega trenja vedno večji od koeficienta dinamičnega trenja.

Ob predpostavki, da je skupna teža vozila in voznika 600 kg in da zadnja kolesa podpirajo 80% teže, določite statično silo trenja med začetkom 4G in statični koeficient trenja med pnevmatikami in pločnikom.

Vam lahko služi: Orion megla: izvor, lokacija, značilnosti in podatkiSlika 4. "Dragster" v času začetka. Vir: Pixabay.

Rešitev

Po drugem zakonu Newtona je nastala sila enaka celotni masi vozila zaradi pospeška, ki ga pridobi.

Ker je vozilo v navpičnem ravnovesju, se normalno in teža razveljavi kot posledična sila trenja f, ki jo pločnik izvaja na kontaktnem območju vlečnih platišč, ostaja pa to:

F = m (4G) = 600 kg (4 x 9,8 m/s²) = 23520 n = 2400 kg-f

To pomeni, da je vlečna sila 2,4 tone.

Trenska sila, ki jo kolesa izvaja na tleh, se vrne nazaj, vendar njegova reakcija, ki je enaka in nasprotna, deluje na pnevmatiki in nadaljuje. To je sila, ki poganja vozilo.

Seveda vso to silo proizvaja motor, ki skozi kolo poskuša potisniti tla nazaj, a kolesa in tla povezujejo s silo trenja. 

Za določitev koeficienta statičnega trenja uporabimo dejstvo, da je pridobljeno F najvišja možna trenja, saj smo na najvišji meji pospeška, torej:

F = μ_in N = μE (0,8 mg)

Dejstvo, da vlečna zadnja kolesa podpirajo 0,8 -krat večjo težo. Odstranjevanje koeficienta trenja se dobi:

μ_in = F / (0,8 mg) = 23520 n / (0,8 x 600 kg x 9,8 m / s^2) = 5.

Zaključek: μ_in = 5.

Reference

1. Alonso m., Finn e. 1970. Fizika zvezek I: Mehanika. Interameriški izobraževalni sklad s.Do.
2. Bauer, w. 2011. Fizika za inženiring in znanosti. Zvezek 1. MC Graw Hill.
3. Hewitt, str. 2012. Konceptualna fizikalna znanost. Peta izdaja.
4. Rex, a. 2011. Osnove fizike. Pearson. 190-200.
5. Mladi, Hugh. 2015. Univerzitetna fizika s sodobno fiziko. 14. izd. Pearson.