Kakšen je dejavnik sorazmernosti? (Rešene vaje)

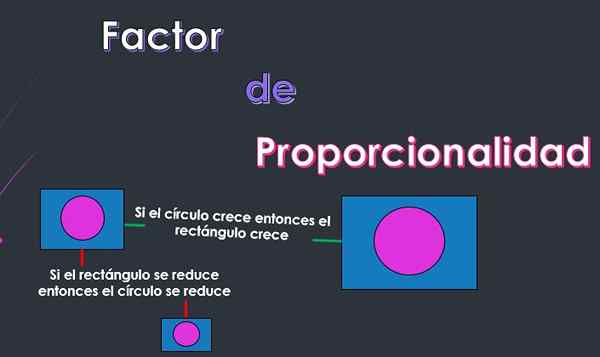
On Faktor sorazmernosti o konstanta sorazmernosti je številka, ki bo pokazala, koliko se drugi predmet spremeni v zvezi s spremembo, ki jo je utrpel prvi predmet.

Na primer, če se reče, da je dolžina stopnišča 2 metra in da je senca, da je ta projekti 1 meter (faktor sorazmernosti je 1/2), potem če se stopnišče zmanjša na dolžino 1 metra, the Senca bo proporcionalno zmanjšala svojo dolžino, zato bo dolžina sence 1/2 metra.

Če se nasprotno stopnišče poveča na 2.3 metre, dolžina sence bo 2.3*1/2 = 1.15 metrov.

Sorazmernost je stalen odnos, ki ga je mogoče vzpostaviti med dvema ali več predmetih, tako da če eden od predmetov doživi kakršno koli spremembo.

Na primer, če se reče, da sta dva predmeta sorazmerna glede na njegovo dolžino, bo imela, če se objekt poveča ali zmanjša svojo dolžino, potem se bo tudi drugi objekt povečal ali zmanjšalo svojo dolžino sorazmerno.

Koncept faktorja sorazmernosti

Faktor sorazmernosti je, kot je prikazano v zgornjem primeru, konstanta, s katero se mora pomnožiti, da dobimo drugo velikost.

V prejšnjem primeru je bil faktor sorazmernosti 1/2, saj je stopnišče "X" izmerilo 2 metra in senca "Y" izmerila 1 meter (polovica). Zato morate y = (1/2)*x.

Ko se torej spremeni "x", se potem spremeni tudi "y". Če je "y" tisti, ki se spremeni, potem se bo spremenil tudi "x", vendar je faktor sorazmernosti drugačen, v tem primeru bi bil 2.

Vaje sorazmernosti

- Prva vaja

Juan želi pripraviti torto za 6 ljudi. Recept, ki ga ima Juan, pravi, da ima torta 250 gramov moke, 100 gramov masla, 80 gramov sladkorja, 4 jajca in 200 mililitrov mleka.

Preden je začel pripravljati torto, je Juan spoznal, da je recept, ki ga ima za torto za 4 ljudi. Kakšne bi morale biti veličine, ki jih mora uporabljati Juan?

Rešitev

Tu je sorazmernost naslednja:

4 osebe - 250 g moke - 100 g masla - 80 g sladkorja - 4 jajca - 200 ml mleka

6 oseb -?

Faktor sorazmernosti v tem primeru je 6/4 = 3/2, kar bi lahko razumeli, kot da ga najprej razdelimo s 4, da dobimo sestavine na osebo, nato pa pomnožite s 6, da torto naredimo za 6 ljudi.

Z množenjem vseh količin za 3/2 so sestavine za 6 ljudi:

6 ljudi - 375 g moke - 150 g masla - 120 g sladkorja - 6 jajc - 300 ml mleka.

- Druga vaja

Dva vozila sta enaka, razen svojih pnevmatik. Polmer pnevmatik vozila je enak 60 cm, polmer drugih pnevmatik vozila pa je enak 90 cm.

Če morate po ogledu dati količino krogov, ki so jih pnevmatike z manj polmera dali, je bilo 300 krogov. Koliko zavojev je dalo največje radijske pnevmatike?

Rešitev

V tej vaji je konstanta sorazmernosti enaka 60/90 = 2/3. Če so radijske manjše pnevmatike dale 300 krogov, potem so pnevmatike z najvišjim radiom dale 2/3*300 = 200 krogov.

- Tretja vaja

Znano je, da so trije delavci v 5 urah naslikali 15 -kvadrat. Koliko lahko v 8 urah pobarvajo 7 delavcev?

Rešitev

Podatki v tej vaji so:

3 delavci - 5 ur - 15 m² stene

In tisto, kar se sprašuje, je:

7 delavcev - 8 ur -- ? M² stena.

Lahko vprašate, koliko bi 3 delavci slikali v 8 urah? Če želite to vedeti, se vrstica podatkov, ki jo dobavi faktor proporcije 8/5, pomnoži. To kaže kot rezultat:

3 delavci - 8 ur - 15*(8/5) = 24 m² stene.

Zdaj želite vedeti, kaj se zgodi, če se število delavcev poveča na 7. Da bi vedel, kakšen učinek proizvede količino stene, naslikano s faktorjem 7/3. To daje končno rešitev:

7 delavcev - 8 ur - 24*(7/3) = 56 m² stene.

Reference

1. Cofré, a., & Tapia, L. (devetnajst devetdeset pet). Kako razviti matematično logično sklepanje. Univerzitetni uvodnik.
2. Napredna fizika Telerasporte. (2014). Edu Nasz.
3. Giancoli, d. (2006). Fizika zvezek I. Pearson Education.
4. Hernández, J. d. (s.F.). Matematični zvezek. Prag.
5. Jiménez, J., Rofríguez, m., & Estrada, r. (2005). Matematika 1 sep. Prag.
6. Neuhauser, c. (2004). Matematika za znanost. Pearson Education.
7. Peña, m. D., & Muntaner, do. R. (1989). Fizikalna kemija. Pearson Education.
8. Segovia, b. R. (2012). Matematične dejavnosti in igre z Miguelom in Lucía. BALDOMERO RUBIO SEGOVIA.
9. Tocci, r. J., & Widmer, n. S. (2003). Digitalni sistemi: načela in aplikacije. Pearson Education.