Trigonometrične omejitve, kako jih rešiti, rešene vaje

The Trigonometrične meje So meje funkcij, tako da te funkcije tvorijo trigonometrične funkcije.

Obstajata dve definiciji, ki morata biti znana, da razumeta, kako se izvaja izračun trigonometrične meje. Te definicije so:

- Mejo funkcije "f", kadar je "x" nagiba k "b": sestavljena je iz izračuna vrednosti, pri kateri se f (x) približa kot "x" približa "b", ne da bi uveljavil "b".

- Trigonometrične funkcije: Trigonometrične funkcije so sinusne, kosinusne in tangentne funkcije, označene s sin (x), cos (x) in tan (x).

Druge trigonometrične funkcije so pridobljene iz treh zgoraj omenjenih funkcij.

Funkcije omejitve

Za razjasnitev koncepta omejitve funkcije bomo nadaljevali z prikazom nekaj primerov s preprostimi funkcijami.

- Meja F (x) = 3, ko je "x" nagiba k "8", je enaka "3", saj je funkcija vedno konstantna. Ni pomembno, koliko je vredno "x", vrednost f (x) bo vedno "3".

- Omejitev f (x) = x-2, ko se "x" nagiba k "6", je "4". Ker je "x" blizu "6", potem se "x-2" približa "6-2 = 4".

- Meja G (x) = x², kadar je "x" nagiba k "3", je enaka 9, saj se "x" približuje "3", potem pa se "x²" približuje "3² = 9".

Kot je mogoče ugotoviti v prejšnjih primerih, je izračun meje sestavljen iz ocene vrednosti, na katero se "x" nagiba v funkciji, in rezultat bo vrednost meje, čeprav to velja samo za neprekinjene funkcije.

Ali obstajajo bolj zapletene omejitve?

Odgovor je pritrdilen. Prejšnji primeri so najpreprostejši primeri omejitev. V knjigah za izračun so glavne mejne vaje tiste, ki ustvarjajo nedoločnost tipa 0/0, ∞/∞, ∞ -∞, 0*∞, (1)^∞, (0)^0 in (∞)^0.

Vam lahko služi: pitagorejske identitete: demonstracija, primer, vaje

Ti izrazi se imenujejo nedoločenja, saj gre za izraze, ki imajo matematično smisel.

Poleg tega se lahko v vsakem primeru odvisno od funkcij, ki so vključene v prvotno mejo.

Primeri preprostih trigonometričnih omejitev

Za reševanje omejitev je vedno zelo koristno poznati grafe vpletenih funkcij. Spodaj so grafi funkcij sinusa, kosinusa in tangent.

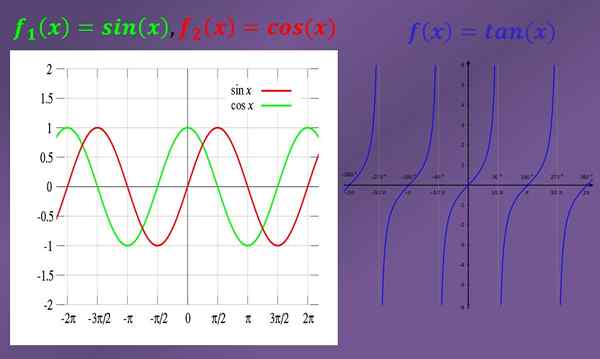
Nekaj ​​primerov preprostih trigonometričnih omejitev je:

- Izračunajte mejo brez (x), ko se "x" nagiba k "0".

Če vidite graf, vidite, da se približuje, če se "x" približuje "0" (tako na levi kot na desni), potem se približuje tudi grafika dojke "0". Zato je meja greha (x), kadar je "x" "0", "0".

- Izračunajte mejo cos (x), ko se "x" nagiba k "0".

Če opazimo graf kosinusa, je razvidno, da je, ko je "x" blizu "0", potem je graf kosinusa blizu "1". To pomeni, da je meja cos (x), kadar je "x" nagiba k "0", enaka "1".

Omejitev lahko obstaja (številka), kot je to v prejšnjih primerih, vendar se lahko zgodi tudi, da ne obstaja, kot je prikazano v naslednjem primeru.

- Meja porjavenja (x), kadar je "x" na levi "π/2" na levi strani, je enaka "+∞", kot je razvidno iz grafike. Po drugi strani pa je meja tan (x), ko se "x" na desno nagiba "-π/2", enaka "-∞".

Trigonometrične omejitve identitete

Dve zelo uporabni identiteti, ko se izračunajo trigonometrične meje: sta:

Vam lahko služi: nelinearno programiranje: metode in vaje

- Omejitev "sin (x)/x", kadar je "x" nagnjena k "0", je enaka "1".

- Omejitev "(1-cos (x))/x", kadar je "x" nagnjena k "0", je enaka "0".

Te identitete se uporabljajo zelo pogosto, ko imate nekakšno nedoločnost.

Rešene vaje

Rešite naslednje omejitve z uporabo zgoraj opisanih identitet.

- Vaja 1

Izračunajte mejo "f (x) = brez (3x)/x", ko se "x" nagiba k "0".

Če je funkcija "F" ovrednotena v "0", dobimo nedoločnost tipa 0/0. Zato moramo poskusiti rešiti to nedoločnost z opisanimi identitetami.

Edina razlika med to mejo in identiteto je številka 3, ki se pojavi znotraj sinusne funkcije. Za uporabo identitete je treba funkcijo "f (x)" prepisati na naslednji način "3*(brez (3x)/3x)". Zdaj sta tako argument dojke kot imenovalec enaka.

Torej, ko se "x" nagiba k "0", je uporaba identitete "3*1 = 3". Zato je meja f (x), kadar je "x" nagiba k "0", enaka "3".

- Vaja 2

Izračunajte mejo "g (x) = 1/x - cos (x)/x", ko se "x" nagiba k "0".

Ko se "x = 0" nadomesti v g (x) in nedoločnost tipa ∞ -∞. Za reševanje se odštejejo frakcije, kar daje kot rezultat "(1-cos (x))/x".

Zdaj je z uporabo druge trigonometrične identitete meja G (x) ta, da je "x" nagiba k "0", enaka 0.

- Vaja 3

Izračunajte mejo "H (x) = 4Tan (5x)/5x", kadar "x" nagiba k "0".

Ponovno, če je H (x) ocenjen v "0", dobimo nedoločnost tipa 0/0.

Prepisovanje kot (5x) kot brez (5x)/cos (5x) Izkaže se, da je H (x) = (brez (5x)/5x)*(4/cos (x))))).

Lahko vam služi: vpisan kot kroga: definicija, teoreme, primeri

Z uporabo meje 4/cos (x), ko se "x" nagiba k "0", je enaka "4/1 = 4" in dobimo prvo trigonometrično identiteto, da je meja H (x), kadar "x" nagiba "0" je enak "1*4 = 4".

Opazovanje

Trigonometrične meje ni vedno enostavno rešiti. V tem članku so prikazani le osnovni primeri.

Reference

1. Fleming, w., & Varberg, D. In. (1989). Prealculus matematika. Prentice Hall Ptr.
2. Fleming, w., & Varberg, D. In. (1989). Matematika predkalkulusa: pristop za reševanje problemov (2, ilustrirano ed.). Michigan: Dvorana Prentice.
3. Fleming, w., & Varberg, D. (1991). Algebra in trigonometrija z analitično geometrijo. Pearson Education.
4. Larson, r. (2010). Prealculus (8 izd.). Cengage učenje.
5. Zvest, J. M., & Viloria, n. G. (2005). Ravna analitična geometrija. Mérida - Venezuela: Venezuelska uredništvo c. Do.
6. Pérez, c. D. (2006). Prequalculus. Pearson Education.
7. Purcell, e. J., Varberg, d., & Rigdon, s. In. (2007). Izračun (Deveta ed.). Dvorana Prentice.
8. Saenz, j. (2005). Diferencialni izračun z zgodnjimi transcendentnimi funkcijami za znanost in inženirstvo (Druga izdaja Ed.). Hipotenuse.
9. Scott, c. Do. (2009). Geometrija kartezijanske ravnine, del: Analitični koniki (1907) (Ponatis ed.). Vir strele.
10. Sullivan, m. (1997). Prequalculus. Pearson Education.