Coplanares točke enačba, primer in rešene vaje

The Točke koplanares Vsi pripadajo isti ravnini. Dve točki sta vedno koplanare, saj te točke definirajo črto, skozi katero prehajajo ravni neskončni. Nato obe točki pripadata vsakemu od načrtov, ki prehajajo skozi črto in bo zato vedno koplanares.

Po drugi strani pa tri točke določijo eno samo ravnino, za katero sledi, da bodo tri točke vedno koplanare do letala, ki jih določajo.

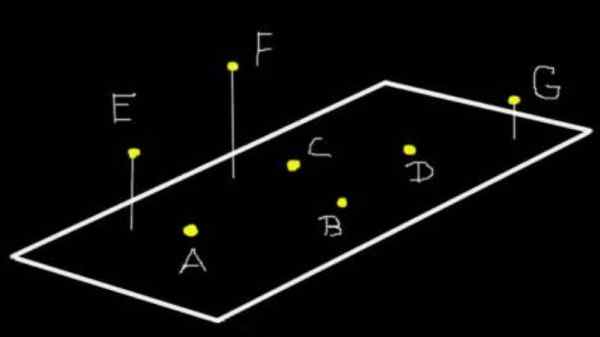
Slika 1. A, B, C in D so koplanare do letala (ω). E, F in G niso koplanare a (ω), če pa so koplanare do letala. Vir: f. Zapata.

Več kot tri točke je lahko koplanar ali ne. Na primer na sliki 1 so točke A, B, C in D koplanare do ravnine (ω). Toda E, F in G niso koplanare A (ω), čeprav so koplanare do letala, ki ga tri definirajo.

[TOC]

Enačba letala dana tri točke

Enačba ravnine, določena s tremi znanimi točkami A, B, C, je matematični odnos, ki zagotavlja, da vsaka točka p generičnih koordinat (x, y, z), ki izpolnjuje enačbo. 

Prejšnja izjava je enakovredna temu, da pravi, da če P koordinate (x, y, z) ustreza enačbi ravnine, potem bo omenjena točka Copatarja s tremi točkami A, B, C, ki je določila ravnino.

Za iskanje enačbe omenjene ravnine začnimo z iskanjem vektorjev Ab in AC:

Ab = [BX - AX, BY - AY, BZ - AZ]

AC = [CX - AX, Cy - AY, CZ - AZ]

Vektorski izdelek Ab X AC Ima za posledico pravokoten ali normalen vektor na ravnino, določeno s točkami A, B, C.

Vsaka točka koordinat (x, y, z) pripada ravnini, če je res, da vektor Ap je pravokotno na vektor Ab X AC, ki je zajamčeno, če je izpolnjeno:

Vam lahko služi: Decagon: redne, nepravilne, lastnosti, primeri

AP • (AB X AC = 0

To je enakovredno temu, da je trojni produkt Ap, Ab in AC Biti ničen. Prejšnja enačba lahko zapišemo na matrični način:

Primer

Naj točke A (0, 1, 2); B (1, 2, 3); C (7, 2, 1) in d (do, 0, 1). Kakšna vrednost bi morala imeti do tako da so štiri točke koplanare?

Rešitev

Če želite najti vrednost a.

Razvoj določitve, ki ga imamo:

A (-1-1) + 1 (-1 -7) -1 (1 -7) = -2a -8 + 6 = -2a -2 = 0

Prejšnja enačba kaže A = -1 Izpolniti enakost. Z drugimi besedami, edini način, kako točka D (do, 0,1) Bodite koplanar s točkami A, B in C je to do Valga -1. Sicer ne bo koplanar.

Rešene vaje

- Vaja 1

Ravnina seka kartezijanske osi x, y, z v 1, 2 in 3. Presečišče omenjene ravnine z osi določa točke A, B in C. Poiščite DZ komponento točke D, katere kartezijanske komponente so:

 D (-DZ, DZ+1, DZ) 

Pod pogojem, da je d koplanar s točkami A, B in C. 

Rešitev

Ko so znani prestrezanje ravnine s kartezijanskimi osi, se lahko uporabi segmentarna oblika ravninske enačbe:

x/1 + y/2 + z/3 = 1

Ker mora točka D pripadati prejšnji ravnini, morate:

-Dz/1 + (dz + 1)/2 + dz/3 = 1

To pomeni:

-Dz + dz/2 + ½ + dz/3 = 1

Dz (-1 + ½ + ⅓) = ½ 

Dz (-1/6⅙) = ½ 

Dz = -3 

Iz zgoraj navedenega izhaja, da je točka D (3, -2, -3) povezati z točkami A (1, 0, 0); B (0, 2, 0) in C (0, 0, 3).

Lahko vam služi: Trikotna merila podobnosti

- Vaja 2

Ugotovite, ali točke A (0, 5, 3); B (0, 6, 4); C (2, 4, 2) in D (2, 3, 1) sta koplanares.

Rešitev

Oblikujemo matrico, katere vrste so koordinate D-A, B-A in C-A. Potem se izračuna determinant in preveri, ali nič.

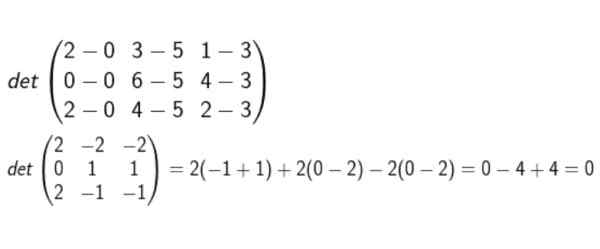
Po izvedbi vseh izračunov se sklepa, da so koplanares.

- Vaja 3

Dve vrstici sta podani v vesolju. Ena od njih je črta (r), katere parametrična enačba je:

(R): x = 1 + 2 λ; y = 1 - λ; Z = 1

In druga je črta (-e), katerih enačba je:

(S): x + 2 y = 1; Z = -1

Dokažite, da sta (r) in (i) koplanarium naravnost, torej v isti ravnini.

Rešitev

Začnimo samovoljno dve točki na črti (R) in dve na vrsti:

Naravnost (r): λ = 0; A (1, 1, 1) in λ = 1; B (3, 0, 1)

Naredimo x = 0 na vrstici=> y = ½; C (0, ½, -1). In na drugi strani, če to storimo y = 0 => x = 1; D (1, 0, -1).

To pomeni, da smo vzeli točke A in B, ki pripadata črti (R), in točkam C in D, ki spadata v črto (-e). Če so te točke koplanare, potem bosta tudi obe vrstici.

Zdaj se odločimo, da bomo pokazali, kako se vrti in nato najdemo koordinate vektorjev Ab, AC in Oglas. Na ta način dobite:

B - A: (3-1, 0 -1, 1 - 1) => Ab= (2, -1, 0)

C -A: (0-1, 1/2 -1, -1 -1) => AC= (-1, -1/2, -2)

D -A: (1-1, 0 -1, -1 -1) => Oglas= (0, -1, -2)

Naslednji korak je graditi in izračunati determinant, katerega prva vrstica so vektorski koeficienti Ab, Druga vrstica so tiste AC in tretjo vrsto vektorja Oglas:

Vam lahko služi: Miletus tak teorem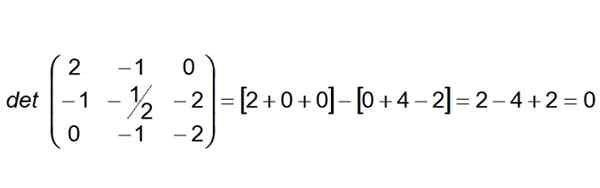

Ker se determinant izkaže za nične, potem lahko sklepamo, da so štiri točke koplanarios. Poleg tega lahko rečemo, da so črte (r) in (i) tudi koplanare.

- Vaja 4

Črte (r) in (i) so koplanare, kot je prikazano v vaji 3. Poiščite enačbo ravnine, ki jih vsebuje.

Rešitev

Točke A, B, C popolnoma definirajo to ravnino, vendar želimo naložiti, da vsaka točka X koordinat (x, y, z) pripada istemu.

X - a: (x -1, y -1, z - 1) => Sekira= (X -1, y -1, z -1)

B - A: (3-1, 0 -1, 1 - 1) => Ab= (2, -1, 0)

C -A: (0-1, 1/2 -1, -1 -1) => AC= (-1, -1/2, -2)

Tako da X pripada ravnini, ki jo določa A, B, C in v kateri so vsebovane črte (R) in (S) Sekira, v drugem Ab In v tretjem tistih AC:

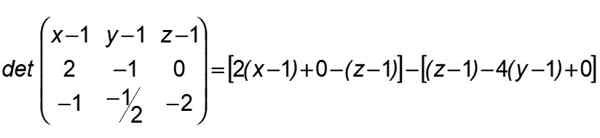
Po tem rezultatu se na ta način združimo:

2 (x-1) + 4 (y-1) -2 (z-1) = 0

In takoj je videti, da ga je mogoče napisati tako:

x - 1 + 2y - 2 - z + 1 = 0

Zato je x + 2y - z = 2 enačba ravnine, ki vsebuje črte (r) in (S).

Reference

1. Fleming, w. 1989. Prealculus matematika. Prentice Hall Ptr.
2. Kolman, b. 2006. Linearna algebra. Pearson Education.
3. Zvest, J. M. 2005. Ravna analitična geometrija. Mérida - Venezuela: Venezuelska uredništvo c. Do.
4. Navarro, Rocio. Vektorji. Obnovi se od: Knjige.Google.co.pojdi.
5. Pérez, c. D. 2006. Prekalenkulacija. Pearson Education.
6. Prenowitz, w. 2012. Osnovni koncepti geometrije. Rowman & Littlefield.
7. Sullivan, m. 1997. Prekalenkulacija. Pearson Education.