Primeri notranje in zunanje konjugirane kote, vaje

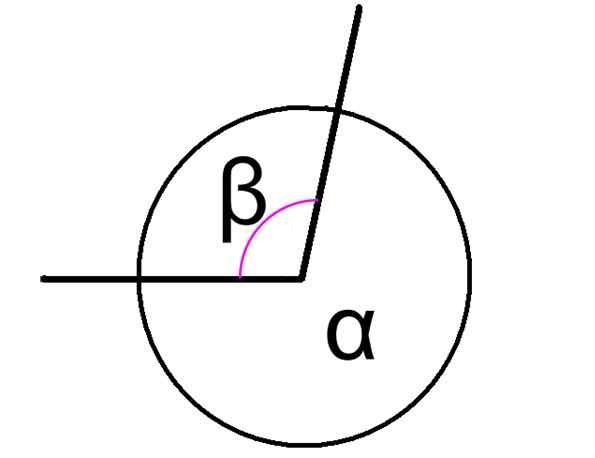
The konjugirani koti Oni so tisti, ki so dodani kot rezultat 360 °, ne glede na to, ali so ti koti sosednji ali ne. Slika 1 prikazuje dva konjugirana kota, označena kot α in β.

V tem primeru imata kota α in β na sliki skupno točko in njihove strani so pogoste, zato so sosednje. Razmerje med njimi je izraženo na naslednji način:

α + β = 360 °

Slika 1. Dva konjugirana osrednja kota, vsota. Vir: Wikimedia Commons. Noben strojno berljiv avtor ni zagotovil. Thiago R Ramos je domneval (na podlagi zahtevkov za avtorske pravice). [CC BY-SA 3.0 (http: // creativeCommons.Org/licence/by-sa/3.0/)] To je razvrstitev kotov po vsoti. Druge pomembne opredelitve vključujejo komplementarni koti, katere vsota je 90 ° in dodatni koti, kar šteje 180 °.

Po drugi strani pa razmislimo o dveh vzporednih črtah, ki jih razrežemo secan, katerih razpoloženje je takrat prikazano:

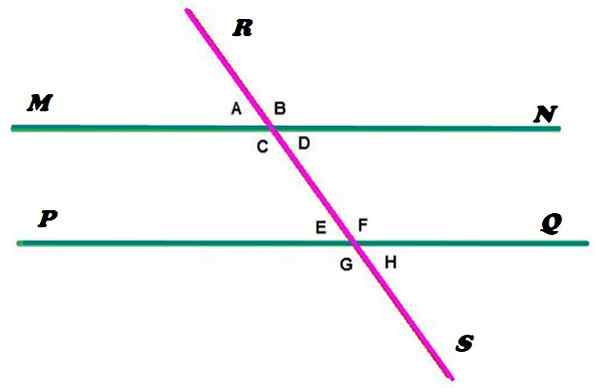Slika 2. Vzporedne črte, ki jih razreže secat. Vir: f. Zapata.

Črte MN in PQ sta vzporedni, medtem ko se linija RS suši in seka vzporednice v dveh točkah. Kot je razvidno, ta konfiguracija določa tvorbo 8 kotov, na katere je bila označena z drobnimi črkami.

No, v skladu z definicijo, podano na začetku, so koti A, B, C in D konjugirani. In na enak način sta E, F, G in H, saj sta oba primera izpolnjena:

A+b+c+d = 360 °

In

E+F+G+H = 360 °

Za to konfiguracijo sta dva kota konjugirana, če sta na isti strani glede na sušenje RS in oba sta notranja ali zunanja. V prvem primeru se govori o kotih Notranji konjugati, Medtem ko so v drugem, so koti zunanji konjugat.

[TOC]

Primeri

Na sliki 2 so zunanji koti tisti, ki so zunaj regije, ki jih omejujeta Mn in PQ linije, so koti A, B, G in H. Medtem ko so koti, ki sta med obema vrsticama, C, D, E in F.

Vam lahko služi: Coplanares Točke: enačba, primer in rešene vaje

Zdaj je treba analizirati, kateri koti so na levi in ​​kateri desno od secata.

Na levi strani Rs so koti A, C, E in G. In na desni so B, D, F in H.

Takoj nadaljujemo z določitvijo parov konjugiranih kotov v skladu z opredelitvijo v prejšnjem razdelku:

-A in G, zunanji in levi od Rs.

-D in F, notranja in desno od Rs.

-B in H, zunanji in desno od Rs.

-C in E, notranji in levo od Rs.

Lastnost konjugiranih kotov med vzporednimi črtami

Konjugirani koti med vzporednimi črtami so dodatni, to je, da je njihova vsota enaka 180 °. Na ta način je za sliko 2 izpolnjeno naslednje:

A + g = 180 °

D + F = 180 °

B + H = 180 °

C + E = 180 °

Ustrezni koti pari za vzporedne črte

So tisti, ki so na isti strani sušilne črte, niso sosednji, ena od njih pa je notranja, druga. Pomembno jih je vizualizirati, saj je njihov ukrep enak, saj so nasprotni koti z vrhom.

Vrnitev na sliko 2 so ustrezni koti identificirani kot:

-A in e

-C in g

-B in f

-D in h

Notranji koti štirikotnika

Quadrilaterals so 4 -veliki poligoni, vključno s kvadratom, pravokotnikom, trapezom, paralelogramom in rombom, na primer, na primer. Ne glede na njegovo obliko je v kateri koli od njih izpolnjeno, da je vsota njegovih notranjih kotov 360 °, zato so v skladu z definicijo na začetku.

Poglejmo nekaj primerov štirikotnikov in kako izračunati vrednost njenih notranjih kotov glede na informacije prejšnjih odsekov:

Vam lahko služi: kakšnih je 7 elementov oboda?

Primeri

a) Trije koti kvadrilateralnega ukrepa 75 °, 110 ° in 70 °. Koliko naj meri preostali kot?

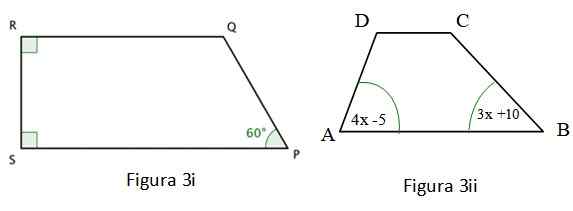
b) Poiščite vrednost kota ∠q na sliki 3 i.

c) Izračunajte, koliko meri kot ∠a slike 3 ii.

Rešitev

Naj bo α manjkajoči kot, izpolni se:

α + 75 º + 110 ° + 70 ° = 360 → α = 105 °

Rešitev b

Slika 3i prikazana je a Trapezoid In dva njegova notranja kota sta ravna, ki sta bila poudarjena z barvnim kvadratom v vogalih. Za to kvadrilateralno preverjeno je naslednje:

∠r + ∠s + ∠p + ∠q = 360 °; ∠s = ∠r = 90 °; ∠p = 60 °

Zato:

∠ Q = 2 x 90 ° + 60 ° = 240 °

Rešitev c

Quadrilateral slike 3 II je tudi trapez, za katerega je izpolnjeno naslednje:

∠a + ∠b + ∠c + ∠d = 360 °

Zato:

4x -5 + 3x + 10 +180 = 360

7x + 5 = 180

X = (180 - 5) / 7

x = 25

Za določitev zahtevanega kota v izjavi se uporablja, da je ∠A = 4x - 5. Zamenjava vrednosti X predhodno izračunanega sledi, da je ∠A = (4 × 25) -5 = 95 °

Vaje

- Vaja 1

Vemo, da je eden od prikazanih zornih kotov vreden 125, in iskanje ukrepov preostalih 7 kotov na naslednji sliki in utemeljitev odgovorov.

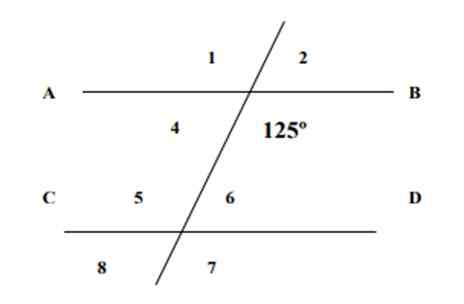Slika 4. Črte in koti vaje 1. Vir: f. Zapata.

Rešitev

Kot 6 in kot 125 sta notranji konjugat, katerega vsota je vredna 180 °, zato glede na lastnost konjugiranih kotov:

∠6 + 125º = 180º → ∠6 = 180 ° - 125 ° = 55 °

Po drugi strani sta ∠6 in ∠8 nasprotna kota z točki, katerih ukrep je enak. Zato ∠8 meri 55 °.

Vam lahko služi: vektorska algebra

Kot je podvržen kot, nasprotuje tudi tolici pri 125, nato pa lahko potrdimo, da je ∠1 = 125 °. Prav tako se lahko pritožimo na dejstvo, da imajo ustrezni pari kotov enak ukrep. Na sliki so ti koti:

∠7 = 125 °

∠2 = ∠6 = 55 °

∠1 = ∠5 = 125 °

∠4 = ∠8 = 55 °

- Vaja 2

Poiščite vrednost x na naslednji sliki in vrednosti vseh kotov:

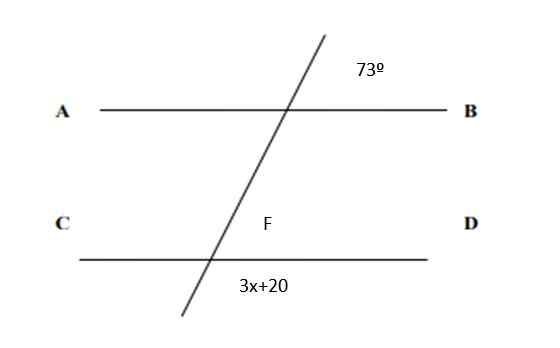Slika 5. Črte in koti za vajo 2. Vir: f. Zapata.

Rešitev

Ker so ustrezni pari, sledi, da je F = 73 °. In na drugi strani je vsota konjugiranih parov 180 °:

3x + 20 ° + 73 ° = 180 °

3x = 180 ° - 73 ° -20 ° = 87

Končno je vrednost X:

x = 87/3 = 29

Kar se tiče vseh kotov, se pojavijo na naslednji sliki:

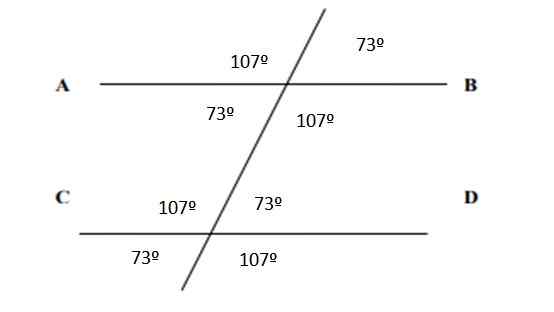Slika 6. Koti, ki imajo vajo 2. Vir: f. Zapata.

Reference

1. Kotne skupine. Komplementarna, dopolnilna in enačbna razlaga. Okrevano od: Thieget.com/
2. Baldor, a. 1983. Ravna in vesoljska in trigonometrijska geometrija. Kulturna domovinska skupina.
3. Corral, m. Matematika librettexts: koti. Okrevano od: matematika.Librettexts.org.
4. Mathmania. Razvrščanje in gradnjo kotov po njihovi meritvi. Okreval od: Mathemania.com/
5. Wentworth, g. Geometrija planeta. Okreval od: Gutenberg.org.
6. Wikipedija. Konjugirani koti. Okrevano od: je.Wikipedija.org.