Pojasnilo kompozita sorazmernosti, tri sestavljene pravila, vaje

The Sestavljena ali večkratna sorazmernost Gre za razmerje med več kot dvema velikosti, kjer je mogoče opaziti neposredno in obratno sorazmernost med podatki in neznanim. Gre za naprednejšo različico preproste sorazmernosti, čeprav so tehnike, uporabljene v obeh postopkih, podobne.

Na primer, če je za prenos 10 ton blaga v 3 urah potrebno 7 ljudi, lahko sestavljeno sorazmernost uporabite za izračun, koliko ljudi bo potrebnih za prenos 15 ton v 4 urah.

Vir: Pixabay.com

Če želite odgovoriti na to vprašanje, je primerno narediti tabelo vrednosti za preučevanje in povezovanje velikosti in neznank.

Analizirajo se vrste odnosov med vsako magnitudo in sedanjo neznano, kar v tem primeru ustreza številu ljudi, ki bodo delali.

Ko se teža blaga povečuje, se poveča tudi število ljudi, potrebnih za prenos. Zaradi tega je odnos med težo in delavci neposreden.

Po drugi strani pa se s povečanjem števila delavcev delovni čas zmanjšuje. Zaradi tega je odnos med ljudmi in delovnim časom obratno.

[TOC]

Kako izračunati sestavljene proporcionalnosti

Za reševanje primerov, kot je prej, se večinoma uporablja metoda treh sestavljenih pravil. To je sestavljeno iz vzpostavljanja vrst razmerij med magnitudami in neznanimi ter nato predstavljati izdelek med ulomki.

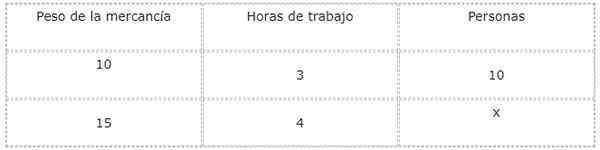
Glede na začetni primer so organi, ki ustrezajo tabeli vrednosti, organizirani na naslednji način:

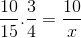
Toda pred reševanjem in čiščenjem neznanega je treba frakcije, ki ustrezajo obratnemu razmerju. Da za ta primer ustreza časovni spremenljivki. Na ta način bo operacija, ki jo je treba rešiti,:

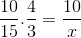
Katerih edina razlika je naložba deleža, ki ustreza spremenljivemu času 4/3. Vrednost X se uporablja in jasna.

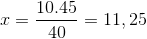
Tako je potrebnih več kot enajst ljudi za prenos 15 ton blaga v 4 urah ali manj.

Pojasnilo

Sorazmernost je stalna povezava med velikostmi, ki so podvrženi spremembam, kar bo simetrično za vsako od vpletenih velikosti. Obstajajo neposredno in obratno sorazmerna razmerja, s čimer določajo parametre preproste ali sestavljene sorazmernosti.

Usmerite tri pravilo

Sestavljen je iz razmerja deleža med spremenljivkami, ki predstavljajo enako vedenje, ko je spremenjena. Je zelo pogost pri izračunu odstotkov, povezanih z različnimi stopnjami sto, kjer je cenjena njena temeljna struktura.

Kot primer lahko izračunate 15% od 63. Na prvi pogled omenjenega odstotka ni mogoče videti na preprost način. Toda pri izvajanju pravila treh lahko vzpostavite naslednje razmerje: Če je 100% 63, potem 15%, koliko bo?

Vam lahko služi: faktorski teorem: razlaga, primeri, vaje

100%-63

15%-x

In ustrezna operacija je:

(Petnajst% . 63) / 100% = 9,45

Kadar so poenostavljeni odstotni znaki in je dosežena 9,45, ki predstavlja 15% od 63.

Tri obratno pravilo

Kot že ime pove, je v tem primeru razmerje med spremenljivkami nasprotno. Pred nadaljevanjem izračuna je treba vzpostaviti obratno razmerje. Njegov postopek je homologn trem neposrednim pravilom, z izjemo naložb v delček, ki ga je treba izračunati.

Na primer, 3 slikarji potrebujejo 5 ur za zaključek stene. Koliko ur bi končali 4 slikarji?

V tem primeru je razmerje obratno, saj bi se s povečanjem števila slikarjev delovni čas zmanjšal. Odnos je vzpostavljen;

3 slikarji - 5 ur

4 slikarji- x ure

Ko je razmerje obratno, se vrstni red delovanja obrne. To je pravilen način;

(3 slikarji) . (5 ur) / 4 slikarji = 3,75 ure

Izraz slikarji so poenostavljeni, rezultat pa 3,75 ure.

Stanje

Če želite biti v prisotnosti spojine ali večkratne sorazmernosti, je treba najti obe vrsti razmerja med magnitudami in spremenljivkami.

- Neposredna: Spremenljivka predstavlja isto vedenje kot neznano. To je s povečanjem ali zmanjševanjem enega, drugega pa je enako spremenjen.

- Inverzno: spremenljivka predstavlja vedenje Antonim neznanim. Del, ki definira to spremenljivko v tabeli vrednosti, mora biti obrnjen, da se predstavlja obratno sorazmerno razmerje med spremenljivko in neznano.

Preverjanje rezultatov

Zelo pogosto je zamenjati vrstni red velikosti pri delu s sestavljenimi proporcionalnostmi, za razliko od tega, kar se dogaja v običajnih izračunih razmer, katerih narava je večinoma neposredna in rešena s preprostim trem pravilom.

Zato je pomembno preučiti logični vrstni red rezultatov in preveriti skladnost figur, ki jih je vrglo tri sestavljene pravila.

V prvotnem primeru bi to napako pomenilo pridobitev 20 kot rezultat. To pomeni, da 20 ljudi v 4 urah prenese 15 ton blaga.

Na prvi pogled se ne zdi nori rezultat, vendar je skoraj 200% povečanje osebja (od 7 do 20 ljudi) radovedno, ko je povečanje blaga 50% in celo z večjo mejo časa za izvajanje delo.

Lahko vam služi: splošna enačba parabole (primeri in vaje)

Na ta način logično preverjanje rezultatov predstavlja pomemben korak z izvajanjem pravila treh sestavkov.

Odmik

Čeprav je bolj osnovna narava glede matematične tvorbe, je očist pomemben korak v primerih sorazmernosti. Napačen odmik zadostuje za razveljavitev kakršnega koli rezultata, pridobljenega v vrstnem redu treh preprostih ali spojin.

Zgodovina

Pravilo treh je postalo znano na Zahodu prek Arabcev, z več avtorji. Med njimi al-jwarizmi in al-biruni.

Al-Biruni je imel zaradi večkulturnega znanja dostop do obsežnih informacij o tej praksi na potovanjih v Indijo, saj je bil odgovoren za najobsežnejšo dokumentacijo o treh pravilih treh.

V svoji preiskavi se pojavlja, da je bila Indija prvo mesto, kjer je bila skupna uporaba treh pravil. Pisatelj zagotavlja, da je bil tekoče izdelan v svoje neposredne, obratne in celo sestavljene različice.

Natančen datum, ko je tri pravilo postalo del matematičnega znanja Indije, še vedno ni znan. Vendar je bil leta 1881 odkrit najstarejši dokument, namenjen tej praksi, Bakhshalijev rokopis. Trenutno je v Oxfordu.

Številni zgodovinarji matematike zagotavljajo, da ta rokopis izvira od začetka sedanje dobe.

Rešene vaje

Vaja 1

Letalska družba mora preseliti 1535 ljudi. Znano je, da bi s tremi ravninami trajalo 12 dni, da se do zadnjega potnika odnesejo na cilj. 450 več ljudi je doseglo letalsko družbo in 2 letali je ukazano, da sodelujeta s to nalogo. Koliko dni bo letalska družba odpeljala do zadnjega potnika do cilja?

Razmerje med številom ljudi in dnevi dela je neposredno, saj več ljudi bo potrebnih več dni za opravljanje tega dela.

Po drugi strani je razmerje med letali in dnevi obratno sorazmerno. S povečanjem količine letal se potrebni dnevi zmanjšajo za prenos na vse potnike.

Tabela vrednosti, ki se nanašajo na ta primer.

Kot je podrobno opisano v začetnem primeru, je treba štetje in imenovalec vložiti v delček, ki ustreza obratni spremenljivki glede na neznano. Zapuščanje operacije na naslednji način:

Vam lahko služi: izračun pristopov z uporabo diferencialov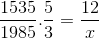

X = 71460/7675 = 9,31 dni

Za prehod na leta 1985 ljudi, ki uporabljajo 5 letal, je potrebnih več kot 9 dni.

Vaja 2

25 -tonska letina koruze se odpelje v tovorne tovornjake. Znano je, da je preteklo leto trajalo 8 ur s plačo 150 delavcev. Če se za to leto plačilne liste povečajo za 35%, koliko časa bo trajalo, da napolnite tovornjake s 40 -tonskim žetvijo?

Preden predstavljate tabelo vrednosti, je treba določiti število delavcev za letošnje leto. To je povečalo 35% začetne številke 150 delavcev. Za to se uporablja neposredno tri pravilo.

100% - 150

35% - x

X = (35 . 100)/100 = 52,5. To je število dodatnih delavcev v zvezi s preteklim letom, pri čemer pridobimo skupno število 203 delavcev, nezadovoljno, da bi zaokrožili pridobljeni znesek.

Določena je ustrezna podatkovna tabela

V tem primeru teža predstavlja spremenljivko neposrednega odnosa z neznanim časom. Po drugi strani pa spremenljivka delavcev upravlja z obratnim odnosom s časom. Večje število delavcev, dan bo krajši.

Upoštevanje teh pomislekov in vlaganje dela, ki ustreza delavcem, se izračuna.

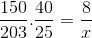
X = 40600 /6000 = 6,76 ure

Dan bo trajal nekaj manj kot 7 ur.

Predlagane vaje

- Določite 73% od 2875.

- Izračunajte količino ur, ki jih Tereza spi, če je znano, da le 7% celotnega spanja. Določite, koliko ur spanja na teden.

- Javni časopis 2000 vsakih 5 ur, pri čemer uporabljam samo 2 tiskana stroja. Koliko izvodov bo ustvarilo v 1 uri, če uporabljate 7 strojev? Kako dolgo bo proizvedlo 10.000 izvodov s 4 stroji?

Reference

1. Encyclopedia Alvarez-i-Inciacion. Do. Álvarez, Antonio Álvarez Pérez. Edaf, 2001.
2. Celoten elementarni in vrhunski priročnik za primarno navodilo: Za uporabo prosilcev za učitelje in zlasti učence običajnih šol v provinci, letnik 1. Joaquín Avendaño. Tiskanje d. Dionisio Hidalgo, 1844.
3. Približek resničnih funkcij. Str. Str. Petrushev, Vasil Atanasov Popov. Cambridge University Press, 3. marca. 2011.
4. Elementarna aritmetika za poučevanje v šolah in šolah v Srednji Ameriki. Darío González. Nasvet. Arenales, 1926.
5. Študija matematike: o študiju in težavah matematike. Augustus de Morgan. Baldwin in Cradock, 1830.