Dinamične značilnosti programiranja, primer, prednosti, slabosti

The Dinamično programiranje To je algoritmski model, ki rešuje zapleten problem z deljenjem na podprobleme in shranjevanje njihovih rezultatov, da se izognete izračunu teh rezultatov.

Ta program se uporablja, kadar lahko težave razdelimo na podobne podprobleme, tako da lahko njihove rezultate ponovno uporabijo. Za večino se ta program uporablja za optimizacijo.

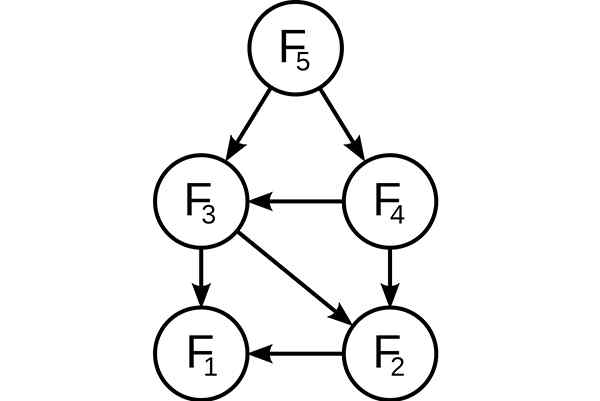
Dinamično programiranje. Podproblemi, nameščeni v nasledstvu Fibonacci. Vir: Wikimedia Commons, AT: Uporabnik: dcoatzee, izsledil uporabnik: STANNERED / JAVNA DOMAIN

Pred reševanjem razpoložljive podprobleme bo dinamični algoritem poskušal preučiti rezultate predhodno rešenih podproblemov. Rešitve podproblemov so združene, da bi dosegli najboljšo rešitev.

Namesto da bi vedno znova izračunali isto podproblemo, lahko vašo rešitev shranite v neki pomnilnik, ko se prvič srečate s to podproblemo. Ko se spet pojavi med rešitvijo drugega podproblema, bo rešitev, ki je že shranjena v pomnilniku.

To je čudovita ideja, da popravite čas s pomnilnikom, kjer lahko pri uporabi dodatnega prostora izboljšate čas, potreben za iskanje rešitve.

[TOC]

Značilnosti dinamičnega programiranja

Naslednje bistvene značilnosti so tiste, ki jih je mogoče uporabiti za dinamično programiranje:

Optimalna podkonstrukcija

Ta značilnost izraža, da je problem z optimizacijo mogoče rešiti s kombiniranjem optimalnih rešitev sekundarnih težav, ki jo nadoknadijo. Te optimalne podstrukture opisujejo rekurzija.

Na primer, v grafu bo na najkrajši poti predstavljena optimalna podkonstrukcija, ki sega od vrha do vrha T:

To pomeni, da lahko na tej najkrajši poti r vzamete katero koli vmesno točko I. Če je R res najkrajša pot, ga lahko razdelimo na Subrutas R1 (od S do I) in R2 (od I do T), tako da so te najkrajše poti med ustreznimi vrhovi.

Zato lahko poiščete najkrajše poti, ki jih lahko raztopino enostavno oblikujete, kar počne algoritem Floyd-Warshall.

Nadgrajeni podproblemi

Prostor podproblemov mora biti majhen. To pomeni, da mora vsak rekurzivni algoritem, ki rešuje problem.

Na primer, za ustvarjanje serije Fibonacci je mogoče upoštevati to rekurzivno formulacijo: fn = f (n-1) + f (n-2), pri čemer upoštevamo kot osnovni primer, ki je f1 = f2 = 1. Potem boste morali: F33 = F32 + F31 in F32 = F31 + F30.

Kot je razvidno, se F31 rešuje v rekurzivnih poddejh obeh F33 in F32. Čeprav je skupno število podproblemov res majhno, če bo sprejeta rekurzivna rešitev, saj bo to na koncu in znova rešilo iste težave.

Vam lahko služi: 7 komponent informacijskega sistema

To se upošteva z dinamičnim programiranjem, zato vsak podproblem reši samo enkrat. To je mogoče doseči na dva načina:

Vrhunski pristop

Če lahko rešitev za katero koli težavo rekurzivno formuliramo z uporabo raztopine njihovih podproblemov in če se ti podproblemi prekrivajo, lahko rešitve za podprobleme enostavno zapomnite ali shranite v tabelo v tabeli.

Vsakič, ko bo iskana rešitev nove podprobleme, jo bomo pregledali v tabeli, če je prej rešena. V primeru, da je rešitev shranjena, bo uporabljena, namesto da bi jo ponovno izračunala. V nasprotnem primeru bo rešena podproblema in raztopino shrani v tabelo.

Vzpon pristop

Ko se rešitev problema rekurzivno oblikuje v smislu njegovih podproblemov, lahko težavo preizkusimo navzgor: najprej bodo poskušali rešiti podprobleme in uporabiti svoje rešitve za doseganje rešitev za največje podprobleme.

To se običajno izvaja tudi v obliki tabele, ki ustvarja iterativne rešitve za vse večje podprobleme z uporabo rešitev za majhne podprobleme. Na primer, če sta vrednosti F31 in F30 že znane, lahko vrednost F32 izračunamo neposredno.

Primerjava z drugimi tehnikami

Pomembna pripadnost problemu, ki jo je mogoče rešiti z dinamičnim programiranjem, je, da bi moral imeti prekrivanje podproblemov. To je tisto, kar razlikuje dinamično programiranje tehnike delitve in osvajanja, kjer ni treba shraniti najpreprostejših vrednosti.

Podobna je kot rekurzija, saj lahko z izračunom osnovnih primerov končno vrednost določimo induktivno. Ta naraščajoči pristop deluje dobro, kadar je nova vrednost odvisna le od predhodno izračunanih vrednosti.

Primer

Najmanjši koraki za dosego 1

Za katero koli pozitivno celotno številko "E" lahko izvedete katero koli od naslednjih treh korakov.

- Odštejte 1 od številke. (E = E-1).

- Če je deljen z 2, je razdeljen z 2 (če je E%2 == 0, potem je E = E/2).

- Če je deljen s 3, je razdeljen s 3 (če je E%3 == 0, potem je E = E/3).

Na podlagi prejšnjih korakov morate najti najmanjšo količino teh korakov in 1. Na primer:

- Če je E = 1, rezultat: 0.

- Če je E = 4, rezultat: 2 (4/2 = 2/2 = 1).

- Ko je E = 7, rezultat: 3 (7-1 = 6/3 = 2/2 = 1).

Pristop

Vedno lahko razmislite o izbiri koraka, ki je N čim nižji in se nadaljuje tako, dokler ne doseže 1. Vendar je razvidno, da ta strategija tukaj ne deluje.

Vam lahko služi: komercialna programska oprema

Na primer, če bi bili E = 10, bi bili koraki: 10/2 = 5-1 = 4/2 = 2/2 = 1 (4 koraki). Vendar je optimalen način: 10-1 = 9/3 = 3/3 = 1 (3 koraki). Zato je treba dokazati vse možne korake, ki jih je mogoče izvesti za vsako vrednost n, pri čemer izberete minimalno količino teh možnosti.

Vse se začne z rekurzijo: f (e) = 1 + min f (e-1), f (e/2), f (e/3), če je E> 1, ki jemlje kot osnovni primer: F (1 ) = 0. Če imate enačbo ponovitve, lahko začnete kodirati rekurzijo.

Vendar pa lahko opazimo, da ima podpredmetne podprobleme. Poleg tega je optimalna rešitev za dani vhod odvisna od optimalne rešitve njegovih podproblemov.

Kot v pomnjenju, kjer so rešitve podproblemov, ki so rešene, shranjene za njihovo uporabo. Ali kot v dinamičnem programiranju se začne od spodaj, napreduje v dani E. Nato obe kodi:

Spomin

Dinamično programiranje navzgor

Prednosti

Ena glavnih prednosti uporabe dinamičnega programiranja je, da pospešuje obdelavo, saj se uporabljajo reference, ki so bile prej izračunane. Kot je rekurzivna programska tehnika, zmanjšuje programske kodne vrstice.

Vorace algoritmos vs dinamično programiranje

Voracious algoritmi so podobni dinamičnemu programiranju v smislu, da sta oba orodja za optimizacijo. Vendar algoritem Voraza išče optimalno rešitev v vsakem lokalnem koraku. To pomeni, da išče pohlepno izbiro z upanjem, da bo našla globalno optimalno.

Zato lahko glasni algoritmi predpostavljajo, da je v tem času videti optimalno, vendar to v prihodnosti postane drago in ne zagotavlja globalnega optimalnega.

Po drugi strani pa dinamično programiranje najde optimalno rešitev za podprobleme in nato informirano izbira s kombiniranjem rezultatov teh podproblemov, da resnično najdete najbolj optimalno rešitev.

Slabosti

- Za shranjevanje izračunanega rezultata vsakega podproblema je potrebno veliko pomnilnika, ne da bi lahko zagotovili, da bo shranjena vrednost uporabljena ali ne.

- Izhodna vrednost se večkrat shrani, ne da bi se med izvedbo kdaj uporabljali v naslednjih podproblemih. To vodi do nepotrebne uporabe pomnilnika.

- V dinamičnem programiranju se funkcije imenujejo rekurzivno. Zaradi tega je pomnilnik baterije ostal v stalnem povečanju.

Rekurzivnost proti dinamičnemu programiranju

Če imate omejen pomnilnik za izvajanje kode in hitrost obdelave ne skrbi, se lahko uporabi rekurzivnost. Na primer, če se razvija mobilna aplikacija, je pomnilnik zelo omejen za izvedbo aplikacije.

Vam lahko služi: mešane naprave: značilnosti in primeri

Če je program zaželeno izvajati hitreje in ni omejitev pomnilnika, je bolje uporabiti dinamično programiranje.

Prijave

Dinamično programiranje je učinkovita metoda za reševanje težav, ki bi se sicer lahko v razumnem času izredno težko rešili.

Algoritmi, ki temeljijo na paradigmi dinamičnega programiranja.

Algoritmi dinamičnega programiranja

Dinamično programiranje je precej učinkovito in zelo dobro služi za široko paleto težav. Številne algoritme je mogoče obravnavati kot aplikacije glasnih algoritmov, kot so:

- Serija številk Fibonacci.

- Hanoi stolpi.

- Vse najkrajše poti pari Floyd-Warshall.

- Nahrbtnik.

- Programiranje projekta.

- Najkrajša pot Dijkstra.

- Nadzor in nadzor letenja robotike.

- Težave z matematično optimizacijo.

- Skupni čas: Delo programirajte za povečanje uporabe CPU -ja.

Serija številk Fibonacci

Številke Fibonacci so številke, ki jih najdemo v naslednjem zaporedju: 0, 1, 1, 3, 5, 8, 13, 21, 34, 55, 89, 144 itd.

V matematični terminologiji je nasledstvo FN fibonaccijevih številk opredeljeno s formulo ponovitve: f (n) = f (n -1) + f (n -2), kjer f (0) = 0 in f (1) = 1 = 1.

Vrhunski pristop

V tem primeru se iskalna matrica z vsemi začetnimi vrednostmi inicializira z -1. Kadar koli je potrebna rešitev podproblema, bo najprej iskana v tej iskalni matriki.

Če obstaja izračunana vrednost, se bo ta vrednost vrnila. V nasprotnem primeru bo rezultat izračunan tako, da ga shranimo v iskalno matrico in ga tako lahko pozneje ponovno uporabimo.

Vzpon pristop

V tem primeru se za isto serijo Fibonacci F (0), nato F (1), F (2), F (3) in tako naprej najprej izračuna. Tako bodo izdelane rešitve podproblemov od spodaj.

Reference

1. Vineet Choudhary (2020). Uvod v dinamično programiranje. Nerazvojnik insider.Vzeto od: razvijalci.co.
2. Alex Allain (2020). Dinamično programiranje v c++. C programiranje. Vzet od: cprogrammming.com.
3. Po oskarici (2020). Ideja o dinamičnem programiranju. Vzeto od: avacademy.com.
4. Aniruddha Chaudhari (2019). Dinamično programiranje in rekurzija | Drugačen. CSE sklad. Vzet od: csestack.org.
5. Code Chef (2020). Za vadnico za dinamično programiranje. Vzet od: codhef.com.
6. Programiz (2020). Dinamično programiranje. Vzeto od: Programiz.com.