Navzkrižni izdelek

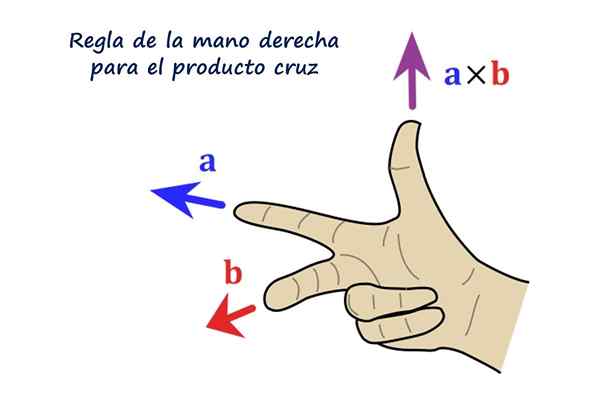
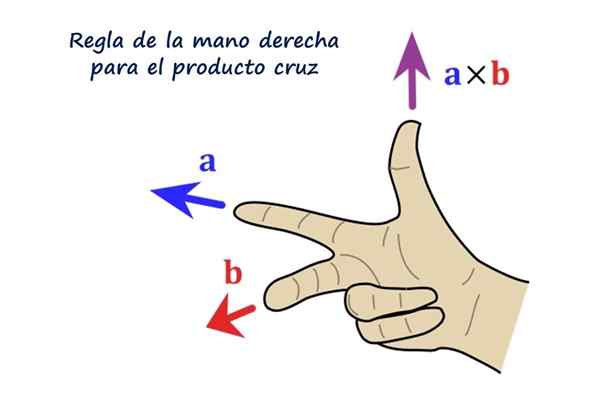Pravo pravilo za vektorski izdelek. Vir: f. Zapata.

Kakšen je križni izdelek ali vektorski izdelek?

On Navzkrižni izdelek, Imenuje se tudi vektorski izdelek, je vrsta izdelka, ki se izvaja med dvema vektorjem in ima za posledico drug vektor, pravokotno na ravnino, ki jo določita prva dva.

Križni izdelek med katerim koli dvema vektorjema do in b, Ima za posledico drug vektor R, Matematično je napisano na naslednji način:

do × b = R

Tako bere: "A cruz b, enak r ".

V tiskanem besedilu so vektorji napisani s krepkimi besedili ali s puščico na črki, da jih ločijo od njihove razsežnosti ali modula. Za to se uporabljajo, zamenljivo, modulske palice in trenutne črke, tako da absolutna vrednost vektorja do Simbol je napisan takole:

│do│ = a

Absolutna vrednost ali modul vektorskega izdelka med dvema vektorji se izračuna tako, da se pomnoži modul obeh vektorjev skozi kota θ med njima:

R = a ∙ b ∙ sen θ

Smer vektorja R Je pravokotna na vektorje do in b. Občutek R Je dextrogyr do proti b In v praksi se določi s pravilom desne roke, ki je sestavljeno iz pozicioniranja indeksa, medija in palca desne roke na naslednji način:

• Kazalec je nameščen po vektorju do
• S srednjim prstom sledi vektorju b
• Palec, razširjen, označuje smer in smer vektorja R.

To naročilo je treba natančno upoštevati, saj vektorski izdelek ni komutativen, to je do × b ≠ b × do In če se vektorji izmenjujejo, pravilnega rezultata ne bomo dobili.

Vam lahko služi: Teorem o obstoju in edinstvenosti: demonstracija, primeri in vaje

Bralcu svetujemo, da postavi desno roko, kot kaže figura, indeks, ki kaže na levo, predstavlja vektor do, Srednji prst sledi b In to kaže neposredno na bralca, končno pa palec označuje navzgor in kaže na smer in smer vektorja do × b = R.

Lastnosti izdelka CRUZ

-Cross ali vektorski izdelek med dvema vektorjem vedno povzroči drug vektor.

-Navzkrižni izdelek ni komutativen, zato: do × b ≠ b × do.

-Za križni izdelek je res, da: do × b = - (b × do). Ta lastnost se imenuje proti sporazumu.

-Nastali vektor vektorja med dvema vektorji je pravokoten (normalen) do omenjenih vektorjev.

-Iz zgoraj navedenega izhaja, da je vektorski izdelek med vektorji z isto smerjo ničen. Še posebej do × A = 0.

-Izdelek za navzkrižni izdelek je v skladu z vsoto distribucijskega zakona: do × (b+c) = do × b + do × c

-Če je m skalar, potem m (do × b) = m do × b = do × m b

Navzkrižni izdelek med enotami

Tri enotne vektorje, imenovani Yo, J in k, Med seboj so pravokotni in označujejo tri pomembne smeri prostora: visoke, široke in globine. Ti naslovi so med seboj pravokotni.

Vektorski izdelek med enotnimi vektorji je enostavno določiti skozi pravilo desne roke in upoštevati lastnosti križnega izdelka:

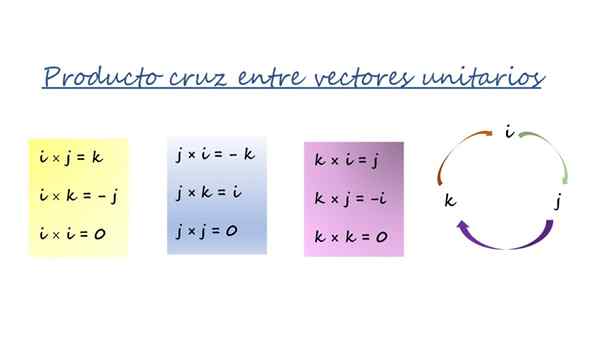Vektorski produkt kartezijanskih enot vektorjev. Vir: f. Zapata.

Tri barvne škatle na sliki so povzete v krogu s puščicami na desni in se uporabljajo na ta način:

-Pri pomnožitvi v smeri puščice je rezultat vektor pred puščico in ima pozitiven znak. Na primer z množitvijo vektorskega J in k, Tretji vektor je Yo, In ko naročilo sledi pomenu puščice, je znak +.

Vam lahko služi: vektorske funkcije

-In če se pomnoži v nasprotni smeri do puščice, je rezultat tretji vektor pred puščico, vendar z negativnim znakom.

Vektorji enot predstavljajo osnovo, zato je mogoče v njih mogoče zapisati kateri koli drug vektor. To močno olajša izračun navzkrižnega izdelka med dvema poljubnimi vektorji v vesolju.

Kako analitično analizirati navzkrižni produkt dveh vektorjev

Ko vektorji do in b V vesolju imajo poljubno smer, s komponentami vzdolž vsakega, lažje je izračunati navzkrižni izdelek na analitični način in jih izraziti v smislu vektorjev enot Yo, J in k:

• do = a_x Yo + do_in J + do_z k
• b = b_x Yo + b_in J + b_z k

Zdaj se uporablja distribucijska lastnost množenja, ki velja tudi za navzkrižni izdelek:

do × b = (a_x Yo + do_in J + do_z k) × (b_x Yo + b_in J + b_z k) =

= (a_x Yo × b_x Yo) + (a_x Yo × b_in J) + (a_x Yo × b_z k) + (a_In J × b_x Yo) + (a_In J × b_in J) + (a_In J × b_z k) + (a_Z k × b_x Yo) + (a_Z k × b_in J) + (a_Z k × b_z k)

Križni izdelki med enakimi enotnimi vektorji se prekličejo, saj so vzporedni vektorji, kar zmanjšuje ta izraz na 6 izrazov:

do × b = (a_x Yo × b_in J) + (a_x Yo × b_z k) + (a_In J × b_x Yo) + (a_In J × b_z k) + (a_Z k × b_x Yo) + (a_Z k × b_in J)

Končno z uporabo zgornje slike vsak izdelek povzroči:

do × b = a_x b_in k + do_x b_z ( - -J) + a_In b_x ( - -k) + a_In b_z Yo + do_Z b_xJ + do_Z b_in ( - -Yo) =

= (a_In b_z - a_Z b_in) Yo + (do_Z b_x - a_x b_z) J + (do_x b_in - a_In b_x) k

Cruz izdelek prek determinanta

Zgoraj navedene formule ni treba zapomniti, vendar priročno uporabiti krog predhodne slike ali preprosto skrbno izvesti spodnje determinant, ki je popolnoma enakovreden:

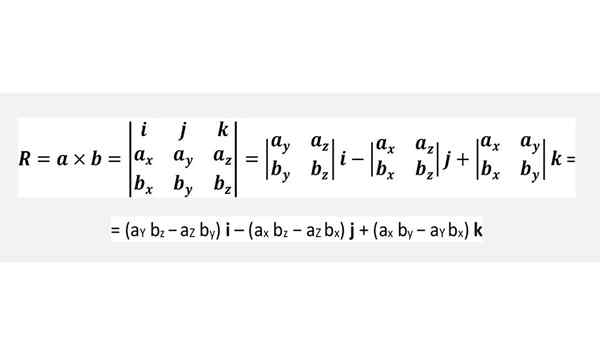
Primer

Ob predpostavki vektorjev do in b so:

• do = 5 Yo - J + 4 k
• b = -Yo + 0J +7 k

Križni izdelek med njimi se izračuna z identifikacijo in zamenjavo ustreznih koordinat:

Vam lahko služi: hiperbolični paraboloid: definicija, lastnosti in primeri

do_x = 5; do_in = −1; do_z = 4; b_x = −1; b_in = 0: b_z = 7

do × b = [(−1) ∙ 7 - 4 ∙ 0] Yo + [(4 ∙ (−1) - 5 ∙ 7) J + [5 ∙ 0 - (−1) ∙ (−1)] k = [−7 - 0] Yo + [(−4 - 35) J + [0 - 1] k =

= (−7) Yo - 39 J - k

Določilna metoda ponuja enak rezultat.

Vaja

Izračunajte po determinanti, navzkrižni izdelek med vektorji:

• ali = 2 Yo +J + 5 k
• v = Yo + 4J +7 k

In določite območje paralelograma, ki ga podredi prejšnji vektorji, kot je prikazano na sliki:

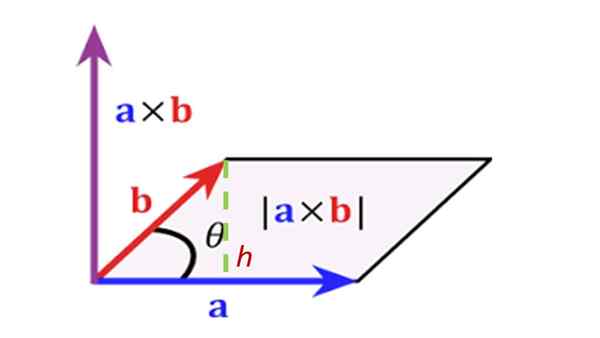
Rešitev

Vrednosti koordinat vektorjev se v določitvi nadomestijo:

Določeno območje paralelograma je modul vektorskega izdelka med njimi, ki ima: r = 17.3 enote območja.