Formula in enačbe pogojne verjetnosti, lastnosti, primeri

The pogojna verjetnost To je možnost pojavljanja določenega dogodka, saj se drugi pojavi kot pogoj. Te dodatne informacije lahko (ali morda ne) spremenijo zaznavanje, da se bo nekaj zgodilo.

Na primer, lahko se vprašamo: "Kakšna je verjetnost, da bo danes deževalo, saj pred dvema dnevoma ne dežuje?". Dogodek, za katerega želimo vedeti, da je verjetno, da danes dežuje, in dodatne informacije, ki bi pogojevale odgovor, so, da "pred dvema dnevoma ne dežuje".

Slika 1. Verjetnost, da danes dežuje, odkar je včeraj deževalo, je tudi primer pogojne verjetnosti. Vir: Pixabay.

Biti Verjetnostni prostor Sestavljen iz ω (vzorčni prostor), ℬ (naključni dogodki) in p (verjetnost vsakega dogodka), ter dogodki A in B, ki pripadata ℬ.

Pogojena verjetnost, ki se pojavi, saj je B, ki je označena kot P (A│B), opredeljena na ta način:

P (a│b) = p (a∩b) / p (b) = p (a in b) / p (b)

Kjer: p (a) je verjetnost pojava a, p (b) verjetnost dogodka B in se razlikuje od 0, P (A∩B) ,, verjetnost, da se zgodita oba dogodka (skupna verjetnost).

To je izraz za Bayesovo izrek, ki se uporabljata za dva dogodka, ki sta ga leta 1763 predlagala angleški teolog in matematik Thomas Bayes.

[TOC]

Lastnosti

-Vsa pogojna verjetnost je med 0 in 1:

0 ≤ p (a│b) ≤ 1

-Verjetnost, da se bo dogodek zgodil, ker se ta dogodek zgodi, je očitno 1:

P (a│a) = p (a∩a) / p (a) = p (a) / p (a) = 1

-Če sta dva dogodka ekskluzivna, torej dogodki, ki se ne morejo zgoditi hkrati, potem je pogojna verjetnost, da se eden od njih zgodi, 0, saj je križišče nično:

P (a│b) = p (a∩b) / p (b) = 0 / p (b) = 0

-Če je B podskupina A, je tudi pogojna verjetnost 1:

Vam lahko služi: Toroid ali Toro Dona

P (b│a) = p (a∩b) / p (a) = 1

Pomembno

P (A│B) Na splošno ni enak P (B│A), zato morate pri iskanju pogojne verjetnosti paziti, da ne boste zamenjali dogodkov.

Splošno pravilo množenja

Velikokrat želite najti skupno verjetnost P (A∩B), namesto pogojne verjetnosti. Torej, skozi naslednji izrek:

P (a∩b) = p (a in b) = p (a│b). P (b)

Teorem se lahko razširi za tri dogodke A, B in C:

P (a∩b∩c) = p (a in b in c) = p (a) · p (b│a) · p (c│a∩b)

In tudi za več dogodkov, na primer₁, Do₂, Do₃ In še več, lahko se izrazi na naslednji način:

P (a₁∩ a₂ ∩ a₃… ∩ A_n) = P (a₁) . P (a₂│a₁). P (a₃│a₁∩ a₂) ... P (a_n│a₁∩ a₂∩… a_N-1)

Kadar gre za dogodke, ki se pojavljajo v zaporedju in v različnih fazah, je primerno organizirati podatke v diagramu ali tabeli. To olajša vizualizacijo možnosti za dosego zahtevane verjetnosti.

Primeri tega so Diagram drevesa in Tabela ob nepredvidljivih dogodkih. Od enega od njih lahko sestavite drugo.

Primeri pogojne verjetnosti

Poglejmo nekaj situacij, v katerih se verjetnosti dogodka spremenijo s pojavom drugega:

- Primer 1

V sladki trgovini se prodajata dve vrsti tort: ​​jagoda in čokolada. Pri registraciji preferenc 50 strank obeh spolov so bile določene naslednje vrednosti:

-27 žensk, od tega 11 raje jagode in 16 čokoladne torte.

-23 moških: 15 čokolade in 8 jagod.

Verjetnost, da kupec izbere čokoladno torto, je mogoče določiti z uporabo pravila Laplacea, v skladu s katerim je verjetnost katerega koli dogodka:

P = število ugodnih dogodkov/skupno število dogodkov

V tem primeru 50 strank skupno 31 raje čokolado, tako da bi bila verjetnost p = 31/50 = 0.62. To pomeni, da 62% kupcev raje čokoladno torto.

Vam lahko služi: polinomne enačbe

A bi bilo drugače, če bi stranka ženska? To je primer pogojne verjetnosti.

Tabela ob nepredvidljivih dogodkih

Skozi takšno tabelo izrednih dogodkov se vsote zlahka vizualizirajo:

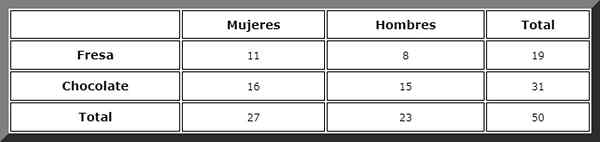
Potem se opazijo ugodni primeri in uporabimo pravilo Laplacea, vendar preden določimo dogodke:

-B je dogodek "ženska stranka".

-A je dogodek "raje čokoladno torto" biti ženska.

Gremo v stolpec z oznako "ženske" in tam vidimo, da je skupno 27.

Potem se v vrstici "čokolade" poišče ugoden primer. Obstaja 16 dogodkov, zato je iskana verjetnost neposredno:

P (a│b) = 16/27 = 0.5924

59.24 % žensk raje čokoladno torto.

Ta vrednost sovpada, ko v nasprotju s prvotno dano definicijo pogojne verjetnosti:

P (a│b) = p (a∩b) / p (b)

Zagotavljamo se skozi pravilo Laplaceja in vrednosti tabele:

P (b) = 27/50

P (a in b) = 16/50

Kjer je p (a in b) verjetnost, da ima stranka raje čokolado in je ženska. Zdaj so vrednosti zamenjane:

P (a│b) = p (a in b)/p (b) = (16/50)/(27/50) = 16/27 = 0.5924.

In dokazano je, da je rezultat enak.

- Primer 2

V tem primeru velja pravilo za množenje. Recimo, da so na razstavi trgovine hlače v treh velikostih: majhne, ​​srednje in velike.

V veliko s skupno 24 hlačami, od katerih je 8 vsake velikosti in vse je mešano. Kakšna bi bila verjetnost, da bosta izvlekli dve in da sta bila oba majhna?

Jasno je, da je verjetnost izvlečenja majhnih hlač v prvem poskusu 8/24 = 1/3. Zdaj je druga ekstrakcija pogojena s prvim dogodkom, saj ko vzamete hlače, jih ni več 24, ampak 23. In če se majhne hlače odstranijo, jih je 7 namesto 8.

Lahko vam služi: Multiplikativno načelo: Tehnike štetja in primeri

Dogodek A je vzeti majhne hlače, saj je v prvem poskusu vzel še enega. In dogodek B je prva hlača do prvega. Zato:

P (b) = 1/3; P (a│b) = 7/24

Končno s pravilom množenja:

P (a∩b) = (7/24).(1/3) = 7/72 = 0.097

Vaja rešena

V študiji točnosti na komercialnih letalskih poletih so na voljo naslednji podatki:

-P (b) = 0.83, je verjetnost, da letalo traja pravočasno.

-P (a) = 0.81, je verjetnost pristanka pravočasno.

-P (b∩a) = 0.78 Verjetnost je, da bo polet prišel pravočasno.

Zahteva se za izračun:

a) Kakšna je verjetnost, da bo letalo takoj pristalo, odkar je pravočasno vzletelo?

b) Zgornja verjetnost je enaka verjetnost, da se je pravočasno pojavila, če vam je uspelo takoj pristati?

c) in končno: kakšna je verjetnost, da bo prišla pravočasno, saj ni prišla pravočasno?

Slika 2. Točnost na komercialnih poletih je pomembna, saj zamude ustvarjajo milijonarje. Vir: Pixabay.

Rešitev

Za odgovor na vprašanje se uporablja opredelitev pogojne verjetnosti:

P (a│b) = p (a∩b) / p (b) = p (a in b) / p (b) = 0.78/0.83 = 0.9398

Rešitev b

V tem primeru se dogodki izmenjujejo v definiciji:

P (b│a) = p (a∩b) / p (a) = p (a in b) / p (a) = 0.78/0.81 = 0.9630

Upoštevajte, da se ta verjetnost nekoliko razlikuje od prejšnje, kot smo že nakazali.

Rešitev c

Verjetnost, da ne bo natančna, je 1 - p (b) = 1 - 0,83 = 0.17, rekli ga bomo p (b^C), Ker je dopolnilni dogodek pravočasno. Pogojna iskana verjetnost je:

P (a│b^C) = P (a∩b^C) / P (b^C) = P (a in b^C)/P (b^C)

Po drugi strani:

P (a∩b^C) = P (čas pristanišča) - p (čas pristanišča in pokuka) = 0.81-0.78 = 0.03

V tem primeru je iskana verjetnost:

P (a│b^C) = 0.03/0.17 = 0.1765

Reference

1. Canavos, g. 1988. Verjetnost in statistika: aplikacije in metode. McGraw Hill.
2. Devore, j. 2012. Verjetnost in statistika za inženirstvo in znanost. 8. Izdaja. Cengage.
3. Lipschutz, s. 1991. Serija Schauma: verjetnost. McGraw Hill.
4. Obregón, i. 1989.Teorija verjetnosti. Uredništvo Limusa.
5. Walpole, r. 2007. Verjetnost in statistika za inženirstvo in znanost. Pearson.
6. Wikipedija. Pogojena verjetnost. Okrevano od: je.Wikipedija.org.