Šesterokotna prizma

Pojasnjujemo, kaj je šesterokotna prizma, njene značilnosti, elemente, območje, vrhove, robove in kako jih izračunati.

Kaj je šesterokotna prizma?

A Šesterokotna prizma To je tridimenzionalno telo, sestavljeno iz dveh šesterokotnikov in strani, oblikovanih kot pravokotnik ali paralelogram. Najdemo ga v naravi, v kristalni strukturi mineralov, kot so na primer berilij, grafit, cink in litij.

Elementi šesterokotne prizme so osnova, obraz, rob, višina, vrhovi, radio in apotem. Od njih lahko izračunate območja in količine.

Zgornja figura prikazuje šesterokotno prizmo s pravokotnimi stranskimi obrazi; to pomeni, Ravna šesterokotna prizma. Šesterokotniki so redni, torej njihove notranje strani in koti so enaki. Vendar so šesterokotni prizmo lahko nepravilni šesterokotniki.

Značilnosti šesterokotne prizme

1- Šesterokotna prizma je tridimenzionalna figura s šesterokotnimi bazami.

2- Obstajajo najrazličnejši predmeti, ki se odzivajo na to definicijo in vendar so precej različni.

Na naslednji sliki so različne šesterokotne prizme: na levi naravni šesterokotni prizmi navadnih obrazov, na desni in navzdol dve šesterokotni prizmi nepravilnih obrazov. Šesterokotnik na dnu prizme spodaj ima posebnost: je konkavno, Kar pomeni, da so nekateri njegovi notranji koti večji od 180 °.

Raznolikost šesterokotnih prizmov. Vir: Wikimedia Commons.

Po drugi strani so šesterokotne baze zgornjih prizmov poligoni konveksna: Vsi notranji koti merijo manj kot 180 °.

Šesterokotni prizmatični elementi

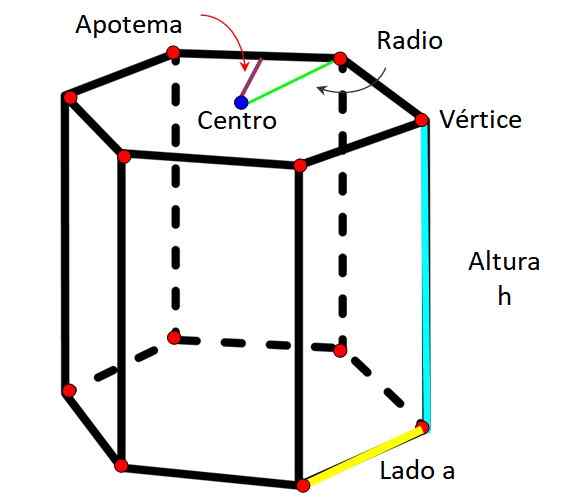Šesterokotni prizmatični elementi. Vir: f. Zapata

Kot vsaka prizma je tudi za šesterokotno prizmo značilna za naslednje elemente:

Vam lahko služi: multiplikativno inverzno: razlaga, primeri, rešene vaje

-Baze: v številu dveh (2), v obliki šesterokotnika in kongruenta, torej enakega merila. Šesterokotni obrazi so lahko redni ali nepravilni.

-Obraze: Šesterokotna prizma ima skupno osem (8) obrazov, ki jih je mogoče šteti s sliko 1. Od 8 obrazov sta dve (2) baze in šest (6) stranskih.

-Rob: Segment se pridruži dvema ali dve strani prizme.

-Višina: To je razdalja med obema obrazoma prizme. Sovpada z dolžino roba v primeru ravne prizme.

-Vertex: Skupna točka med osnovno in dvema stranskima stranema.

Če so baze prizme redne, simetrija figure omogoča določitev dodatnih elementov navadne šesterokotne strani do.

-Radio: To je razdalja, izmerjena od središča šesterokotnika in katerega koli vrha.

-Apotem: To je segment, ki sega od središča šesterokotnega obraza na sredino ene strani.

S pomočjo teh elementov se izračunajo območja in količine, kot bomo videli kasneje.

Formule

Obstajajo številne formule, povezane s šesterokotno prizmo. Služijo za izračun območja svojih stranskih baz in obrazov, njenega prostornine in drugih pomembnih značilnosti. Območja rednega šesterokotnika, nepravilnega šesterokotnika in paralelograma ter oboda so koristna.

Obod ravne figure

To je merilo njegove konture, ki je v primeru poligona, kot je šesterokotnik. Če je šesterokotnik redno stransko do, Obstaja formula za obod Str:

P = 6.do

Redno območje šesterokotnikov

Pokličimo ALS in L_Do Na dolžini apotema. Območje daje:

Vam lahko služi: ne -združeni podatki: primeri in rešeni primeri in vaja

A = p. L_Do/2 = 6a. L_Do/2

Kje Str je obod slike.

Odvisno od velikosti strani do, Območje se lahko izračuna tudi z:

A = 2.5981.do²

Nepravilno območje šesterokotnika

Ni posebne formule, saj je odvisna od razporeditve strani, vendar lahko šesterokotnik razdelimo na trikotnike, izračunamo območje vsakega in jih dodajte.

Druga metoda za iskanje območja je Gaussova determinanta, za katero je treba poznati koordinate šestnajstih vrhov.

Območje paralelograma

A = osnovna x višina

Ja do je osnova in h To je višina, območje je:

A = a.h

Šesterokotno območje prizme

To je vsota območij baz -dva heksagona -in tisti iz obrazov -6 pravokotnikov ali paralelogramov-.

Redno območje šesterokotne prizme

Če ima šesterokotna prizma osnove v obliki rednih šestkotnikov in so stranski robovi pravokotni na te baze, je njegovo območje podano z vsoto:

A = 2 x 2.5981.do² + 6.h

Kje do Je stran šesterokotnika in h To je višina prizme.

Nepravilno in ravno šesterokotno območje prizme

Če so baze nepravilne šesterokotnike, se območje izračuna z:

A = 2a_baza  + Str.h

Kje:

-Do_baza To je nepravilno šesterokotno osnovno območje.

-P je obod osnove.

-H je višina prizme

Točke

Vsak šesterokotni obraz ima 6 vogalov ali vrhov, kar daje skupno 12 vrhov za šesterokotno prizmo.

Robovi

Obstaja formula za iskanje števila robov prizme. Odkril ga je veliki matematik Leonhard Euler (1707-1783) in se imenuje Eulerjev teorem za polihedros. Pravi tako:

Vam lahko služi: algebrsko sklepanje

Če je C število obrazov in količina Vértices V in skupni robovi. Res je, da:

C+V = A+2

Znesek za šesterokotno prizmo so: C = 8 in V = 12. Zato je A:

A = C + V - 2 = 8 + 12-2 = 18

Glasnost

Zvezek V katere koli prizme, bodisi ravne ali poševne, rednih ali nepravilnih obrazov, je podan:

V = osnovno območje x višina

Zato bomo potrebovali formule za območje, ki smo ga videli prej.

Na primer, za ravno šestkotno prizmo, katere baze so redni šesterokotniki, glasnost daje:

V = 2.5981.do².h

Reference

1. Open Reference Math Open. Območje poligona. Okreval od: Mathpenref.com.
2. Wikipedija. Prizma. Okrevano od: je.Wikipedija.com.