Formula hidrostatičnega tlaka, izračun, primeri, vaje

The Hidrostatični tlak To je tisti, ki izvaja tekočino v statičnem ravnovesju kjer koli v notranjosti, bodisi območje, potopljeno vanj, stene posode ali del tekočine, ki je del skupne mase.

Način, kako tekočine izvajajo tlak, se razlikuje od trdnih snovi. Ti izvajajo tlak, vendar tekočina ali plin to stori v vse smeri.

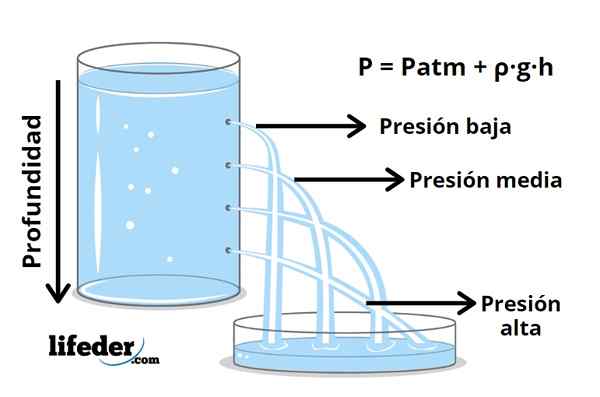
Slika 1- Pri večji globini večji tlak

Ko gre za tekočino, se tlak poveča z globino, kot je znano z izkušnjami, ko potopite v vodo, v kateri se v ušesih čuti povečanje tlaka. Ta tlak izhaja iz teže tekočine in nenehnega gibanja delcev, ki ga sestavljajo, ki nenehno zadenejo površino telesa, potopljene v tekočino.

Če predpostavimo, da je nestisljiva tekočina - kar velja v veliki večini aplikacij, - njegova gostota ostaja konstantna in v tem primeru je tlak linearno odvisen od globine.

[TOC]

Formula

Hidrostatični tlak se izračuna z naslednjim izrazom:

P = p_Bankomat + ρ · g · h

Kje:

-P Tlak, ki se izvaja v točki

-Str_Bankomat Je pritisk atmosfere na prosti površini

-ρ je gostota tekočine

-G je pospešek gravitacije

-H je globina, ki jo želite izračunati hidrostatični tlak 

Formula vključuje učinke atmosfere, vendar veliko tlaka ali manometrov postavlja 0 v atmosferskem tlaku, zaradi česar merijo diferencialni ali relativni tlak Tlak merilnika:

Str_m = ρ · g · h

Kar zadeva pline, jih zelo enostavno stisnemo ali razširimo. Zato je njegova gostota, ki je razlog med maso in prostornino, običajno funkcija drugih parametrov, kot sta nadmorska in temperatura, v primeru atmosferskih plinov.

Lahko vam služi: magnetizacija: orbitalni in vrteni magnetni trenutek, primeri

Tlak, ki ga izvajajo plini, se običajno imenuje Aerostatični tlak, izraz hidrostatični tlak za rezervacije tekočin.

Primeri hidrostatičnega tlaka

Hidrostatični tlak je odvisen samo od globine, zato oblika ali območje dna posode ni pomembna.

Ker je tlak P opredeljen kot pravokotna komponenta sile F na enoto območja A:

P = f/a

Potem je sila, ki jo ima tekočina na dnu posode, lahko drugačna, vendar je porazdeljena po različnih podaljških, tlak, ki je razmerje sile/območja, je enak za točke do iste globine.

Razmislite o zabojnikih slike. Tlak je enak za vse rdeče točke, ki so na isti ravni, čeprav je v centralni vsebniki večja količina tekočine nad to stopnjo -več širine -, od katerih sta cilindrična in tanka cev skrajne levice.

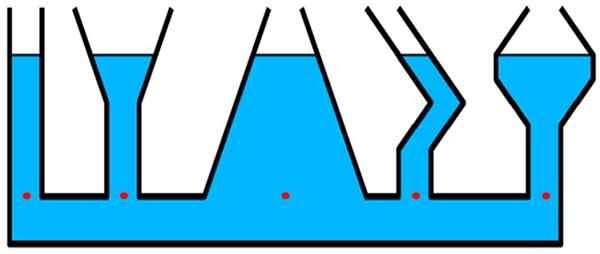Slika 2.- Pritisk na kateri koli od rdečih točk je enak, ne glede na obliko posode. Vir: Wikimedia Commons.

Strukture, kjer je hidrostatični tlak pomemben

-Stene jezu: Čeprav je sila enaka za vse točke ravnega dna, na navpični steni raste, ko se globina povečuje, zato so podporne stene v dnu širše kot v zgornjem delu.

-Na stenah in dnu bazena.

-V zvezdah, kot je naše sonce, kjer hidrostatični tlak uravnoteži silo gravitacije in ohranja zvezdo v operaciji. Ko je omenjeno ravnovesje pokvarjeno, se zvezda zruši in trpi izjemne spremembe v svoji strukturi.

Vam lahko služi: kaj je magnetni trenutek?

-Tekoči rezervoarji za shranjevanje, zasnovani za umor hidrostatičnega tlaka. Ne samo sten, ampak vrata, ki olajšajo polnjenje in ekstrakcijo. Za njegovo zasnovo se upošteva, če je tekočina jedska in tudi tlak in sila, ki jo izvaja v skladu z njegovo gostoto.

-Pnevmatike in baloni, ki so okuženi tako, da se upirajo tlaku tekočine (plina ali tekočine).

-Vsako potopljeno telo, ki doživlja navpični potisk ali "olajšanje" svoje teže, zahvaljujoč hidrostatičnemu tlaku, ki ga izvaja tekočina. To je znano kot Načelo Archimeda.

Vaje

Načelo Archimeda potrjuje, da bo s potopljenjem telesa popolnoma ali delno doživela navpično silo navzgor, znano kot potisk. Obseg potiska je številčno enaka teži volumna vode, ki jo je predmet premikal.

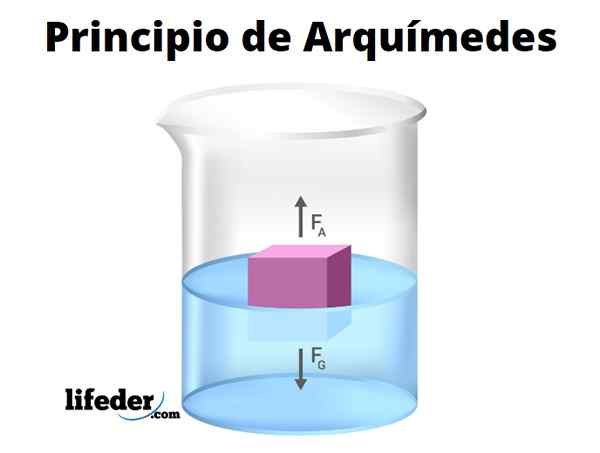
Biti ρ_tekoče Gostota tekočine, v_s Potopljeni volumen, g Pospešek gravitacije in B, velikost potiska, ki jo lahko izračunamo z naslednjim izrazom:

B = ρ_tekoče .V_s .g

- Vaja 1

Pravokoten blok, katerega dimenzije so 2.0 cm x 2.0 cm x 6.0 cm lebdi v sladki vodi z najdaljšo navpično osi. Dolžina bloka, ki izstopa nad vodo, je 2.0 cm. Izračunajte gostoto blokov.

Rešitev

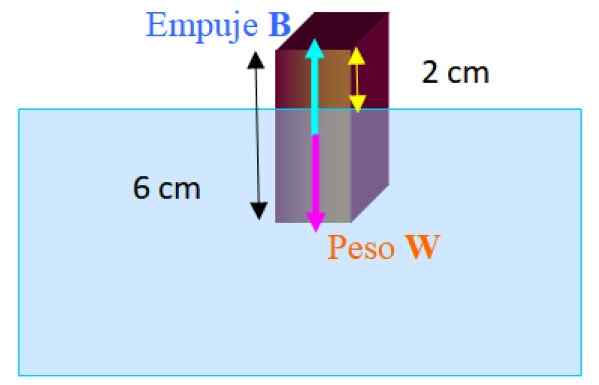Slika 3.- Brezplačen karoserijski diagram za blok, ki lebdi delno potopljen v vodo. Vir: f. Zapata.

Sile, ki delujejo na blok, so teža W navzdol in potisni B navzgor. Ko blok lebdi v ravnovesju, imate:

∑ f_in = B - W = 0

B = w

Obseg teže W je produkt mase m bloka zaradi pospeška gravitacije. Uporabili bomo definicijo gostote ρ_tudi Kot količnik med maso m in glasnost V bloka:

Lahko vam služi: Analiza mrežice: pojmi, metode, primeri

ρ_tudi = m / v → m = ρ_tudi . V

Svoje delo je potis:

B = ρ_tekoče .V_s .g

Izenačujoča velikost potiska in velikosti teže:

ρ_tekoče .V_s .G = ρ_tudi . V.g

Gravitacija se prekliče, ker je dejavnik na obeh straneh in gostota bloka je mogoče očistiti kot:

ρ_tudi = ρ_tekoče . (V_s  / V)

Gostota vode v mednarodnih sistemskih enotah je 1000 kg/m³. Skupni V količini in potopljeni V_s, Izračunajo jih z v = širina x visoka x globina:

V = 2.0 cm x 2.0 cm x 6.0 cm = 24.0 cm³

V_s = 2.0 cm x 2.0 cm x 4.0 cm = 16.0 cm³

Zamenjava vrednosti:

ρ_tudi = ρ_tekoče . (V_s  / V) = 1000 kg/ m³ . (16/24) = 667 kg/m³

- Vaja 2

Izračunajte potopljeni volumski odstotek kosa ledu, ki plava v morski vodi na 0 ° C.

Rešitev

Ledeni lebdi v vodi, saj je njegova gostota nižja: 916.8 kg/m³, kar pomeni, da se širi, ko se ohladi, za razliko od večine snovi, da se, ko segrejejo.

Slika 4. Skoraj celotna količina ledene gore ostane potopljena. Vir: Pixabay.

To je zelo srečna okoliščina za življenje, od takrat pa mase vode zamrznejo le na površini, v globini pa ostanejo tekočine.

Gostota morske vode je nekoliko večja kot pri sladki vodi: 1027 kg/m³. Izračunali bomo volumsko frakcijo v_s  / V:

V_s  / V = ​​ρ_tudi / ρ_tekoče = 916.8 kg/m³  / 1027 kg/ m³ = 0.8927

To pomeni, da približno 89 % ledu ostane pod vodo. Samo 11 % je vidno, ki plava na morju.

Reference

1. Giambattista, a. 2010. Fizika. 2. mesto. Ed. McGraw Hill.
2. Vitez, r.  2017. Fizika za znanstvenike in inženiring: strateški pristop. Pearson.
3. Cimbala, c. 2006. Mehanika tekočin, osnov in aplikacij. MC. Graw Hill.
4. Hibbeler, R. 2015. Mehanika tekočine. 1. Ed. Pearson.
5. Mott, r.  2006. Mehanika tekočine. 4. Izdaja. Pearson Education.
6. Streeter, v. 1999. Mehanika tekočine. McGraw Hill.