Redne lastnosti poligonov, elementi, koti, primeri

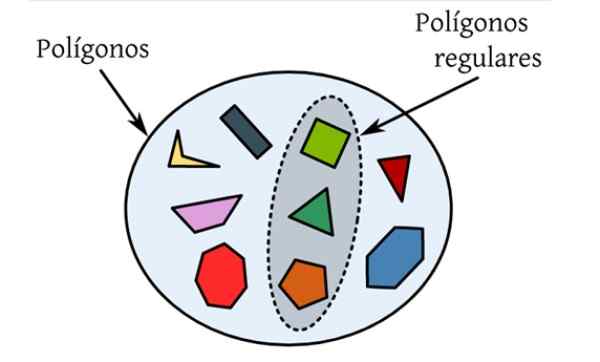
The Redni poligoni Oni so tisti, ki imajo vse svoje strani in enake notranje kote. Na naslednji sliki je nabor različnih poligonov, ki so ravne številke omejene z zaprto krivuljo in samo tisti, ki so izpostavljeni, izpolnjujejo pogoje, ki so redni.

Na primer, enakostranični trikotnik je redni poligon, saj njene tri strani merijo enako, pa tudi njegove notranje kote, ki so vredni 60 °.

Slika 1. Redni poligoni so tisti, katerih stranice in notranji koti so enaki, na primer enakostranični trikotnik in kvadrat. Vir: Wikimedia Commons.

Trg je kvadrilateralen s štirimi stranicami enake mere in katerih notranji koti so 90 °. Sledi navadni pentagon, s petimi stranicami enake velikosti in petimi notranjimi koti 108 °.

Ko je poligon reden, se ta beseda doda v svoje posebno ime, zato imamo običajni šesterokotnik, redni heptagon in tako naprej.

[TOC]

Lastnosti rednih poligonov

Najpomembnejše lastnosti rednih poligonov je mogoče povzeti na naslednji način:

-Strani merijo enako, zato so enakostranski.

-So Equiagularni, No, vsi njegovi notranji koti imajo enako mero.

-Vedno se lahko registrirajo v obodu, kar pomeni, da se popolnoma prilegajo enemu, ki se imenuje Osmerjeni obod.

-Za redni poligon N strani je merilo notranjega kota α:

α = [180 (n-2)]/n

-N-3)/2 diagonale lahko črpate iz vrhov poligona, ne glede na to, ali so redni ali ne.

-Vsota Zunanji koti Je enak 360 °.

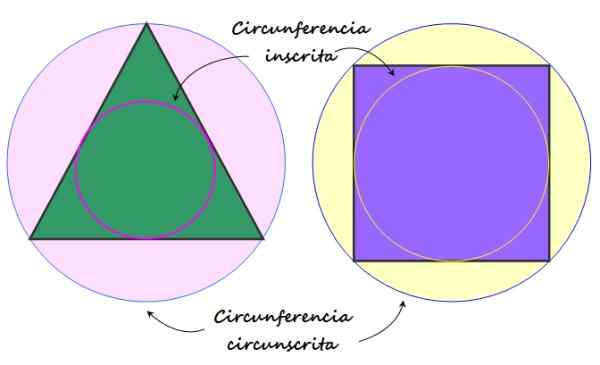Slika 2. Registriran obseg in obod, opisan na redni poligon. Vir: f. Zapata.

Elementi rednega poligona

Nato predstavimo glavne elemente navadnega poligona, ki so vizualizirani na spodnji sliki.

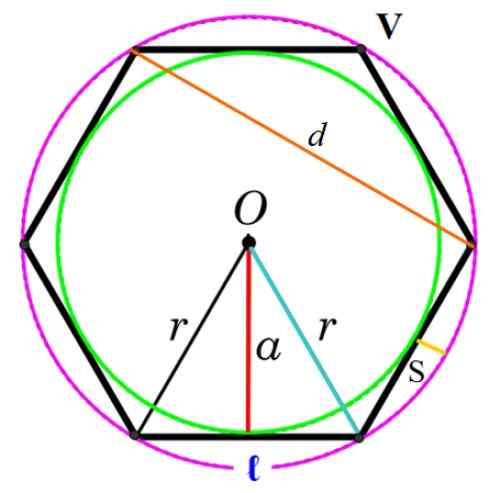Slika 3. Elementi rednega poligona. Vir: f. Zapata.

Vertex

Skupna točka, ki imata dve zaporedni strani, označene kot V na sliki.

Stran

To je segment, ki se pridruži dve zaporedni točki poligona in je označen kot ℓ ali L.

Diagonala

Segment, ki se pridruži dvema ne -zaključljivimi točki poligona, na sliki je označen kot kot d.

Center

To je skupno središče registriranega oboda in omejenega oboda, označeno s pismom ali. To je mogoče razumeti tudi kot edino točko, ki je enakosta tako vrhov kot na srednjih točkah na vsaki strani.

Radio

To je radio r Omejenega obsega in sovpada z razdaljo med O in Vertexom.

Lahko vam služi: aksiomi verjetnosti: vrste, razlaga, primeri, vaje

Apotem

Se imenuje apotem do polmera oboda, vpisanega v poligon, predstavljen na sliki s črko do. Apotem je pravokoten na stran in to združuje s središčnim O (rdeči segment na sliki 3).

Če poznamo polmer r in dolžino strani, se apotem izračuna z:

Ker je apotem v bistvu ena od kategorij pravokotnika trikotnika (glej sliko 3), drugi kateto je vrednost ℓ/2 (polovica ene strani) in hipotenuza radia r poligona.

Ko se teorem pitagore uporablja za omenjeni trikotnik, je ta enačba pridobljena, kar velja ne le za šesterokotnike, ampak za vsak redni poligon.

Osrednji kot

To je kot, katerega točka sovpada s središčem ali katerih strani so segmenti, ki združujejo center z dvema zaporednima točkoma. Njegova mera v seksualnih stopnjah je 360 ​​°/N, kjer n Je število strani poligona.

Sagita

To je razlika med polmerom poligona in apotemom (glej sliko 3). Označevanje sagite kot S:

S = r - a

Obod in območje

Obseg

Enostavno se izračuna z dodajanjem dolžin strani. Ker je katera koli stran enaka dolžina L in obstajajo N strani, je obod P izražen kot:

P = n.L

Območje

V običajnem poligonu je območje A podano z izdelkom med pol-perimetrom (polovico oboda) in dolžino apotema do.

A = p.A /2

Ker je obod odvisen od števila strani n, se izkaže, da:

A = (nl).A /2

Dva navadna poligona imata lahko enak obod, tudi če nimata enakega števila strani, saj bi potem odvisni od dolžine strani.

V knjigi V vaše Zbirka, Aleksandrijski matematik Pappus (290-350), zadnji od velikih grških matematikov antike, je pokazal, da je med vsemi običajnimi poligoni z istim obodom tisti z največjim območjem z največjim številom strani.

Koti

Slika 4 prikazuje ustrezne kote v običajnem poligonu, označene z grškimi črkami α, β in γ.

Osrednji kot

Prej omenjamo osrednji kot, med elementi običajnega poligona, je kot, katerega točka je v središču poligona, in stranice so segmenti, ki združujejo središče z dvema zaporednima točkama.

Za izračun ukrepa osrednjega kota α je 360 ​​° razdeljen na n, število strani. Ali 2π radianov med n:

Vam lahko služi: injektivna funkcija: iz česa je sestavljena, kaj je in primeri

α = 360 °/N

Enakovredno v radianih:

α = 2π /n

Notranji kot ali notranji kot

Na sliki 4 je notranji kot β tisti, katerega točka sovpada z eno od slik in njene strani so tudi stranice slike. Izračuna se v stopinjah SexagesImal z:

β = [180 (n-2)]/n

Ali v radianih, ki uporabljajo:

β = [π (n-2)]/n

Zunanji koti

Označuje jih grško pismo γ. Na sliki je opaziti, da je γ + β = 180 °. Zato:

γ = 180 ° - β

Vsota vseh zunanjih kotov na običajni poligon je 360 ​​°.

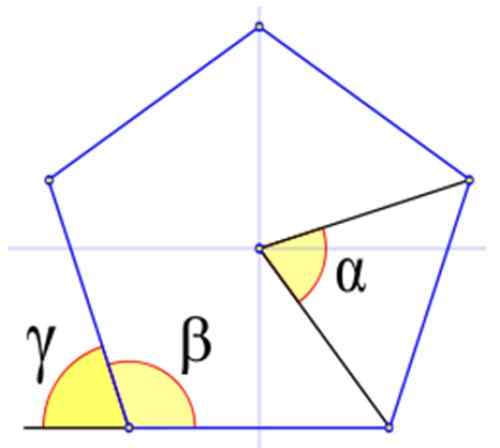Slika 4. Koti v običajnem poligonu, v tem primeru navaden pentagon. Vir: Wikimedia Commons.

Primeri rednih poligonov

Spodaj imamo prvih 8 rednih poligonov. Opažamo, da s povečanjem števila strani poligon postaja vse bolj do oboda, v katerem so registrirani.

Lahko si predstavljamo, da dolžina strani vse bolj majhna in povečata število teh, dobimo obod.

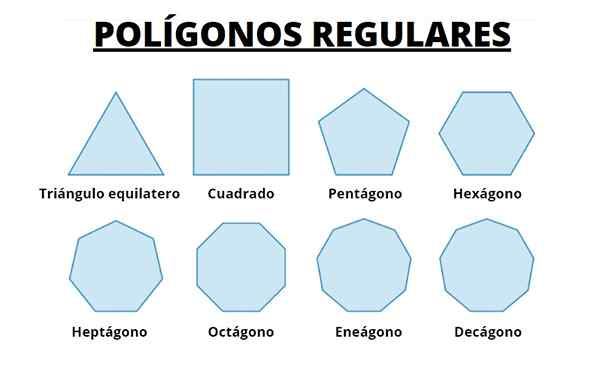Slika 5. Prvih osem rednih poligonov. Vir: Wikimedia Commons.

- Redni poligoni v vsakdanjem življenju in naravi

Redni poligoni najdemo povsod v vsakdanjem življenju in celo v naravi. Poglejmo nekaj primerov:

Prometni signali

V signaliziranju, ki jih vidimo na avtocestah in cestah, obiluje redne poligone, kot so enakostranični, kvadratni in rombski trikotniki. Na sliki 6 vidimo signalni signal z visoko zasnovo.

Slika 5.- Prometni signal z osmerokotno obliko. Vir: Pixabay.

Pohištvo

Nešteto pohištva so na primer kvadratni, kot značilna geometrijska figura, pa tudi številne mize, stoli in banke so kvadratni. Paralelepiped je na splošno škatla z stranicami v obliki pravokotnika (kar ni običajni poligon), lahko pa tudi kvadratno.

Arhitektura in gradnja

Ploščice ali ploščice tal in sten, tako v domovih kot na ulicah, imajo pogosto obliko rednih poligonov.

Tesels so površine, pokrite v celoti s ploščicami, ki imajo raznolike geometrijske figure. S trikotnikom je mogoče narediti kvadrat in šesterokotnike, ki so navadni Tesselve, tisti, ki uporabljajo samo eno vrsto figure za odlično prevleko, brez praznih presledkov (glej sliko 6).

Tudi stavbe uporabljajo redne poligone v elementih, kot so okna in dekoracija.

Slika 6. Kvadratna ploščica. Vir: Pixabay.

- Redni šesterokotniki v naravi

Presenetljivo je, da je redni šesterokotnik poligon, ki se pogosto pojavlja v naravi.

Vam lahko služi: diskretne distribucije

Satja, ki jih čebele izdelujejo za shranjevanje med. Kot je opazil pappus iz Aleksandrije, na ta način čebele optimizirajo prostor, da prihranijo čim več medu.

In v lupini želv in snežinkov obstajajo tudi redni šesterokotniki, ki sprejemajo tudi različne zelo lepe geometrijske oblike.

Vaja rešena

Navadni šesterokotnik je del polmera polmera 6 cm, kot je prikazano na sliki. Kakšna je vrednost senčenega območja?

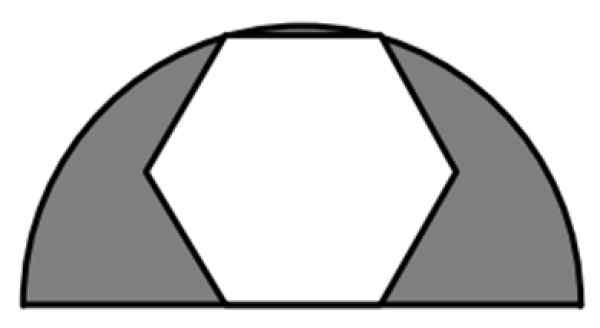Slika 7. Navaden šesterokotnik, registriran v polkrogu. Vir: f. Zapata.

Rešitev

Zasenčeno območje je razlika med polmerom polkroga območja r = 6 cm in polnim območjem šesterokotnika, običajnim 6 -stranskim poligonom. Tako bomo potrebovali formule za območje vsake od teh številk.

Podmestno območje

Do₁ = π r² /2 = π (6 cm)² /2 = 18π cm²

Redno območje šesterokotnikov

Formula za izračun območja rednega poligona je:

A = p.A /2

Kje Str To je obod in do To je apotem. Ker je obod vsota strani, bomo potrebovali vrednost le -teh. Za redni šesterokotnik:

P = 6ℓ

Zato:

A = 6ℓa /2

Če želite najti vrednost strani ℓ, je treba zgraditi pomožne številke, ki jih bomo razložili spodaj:

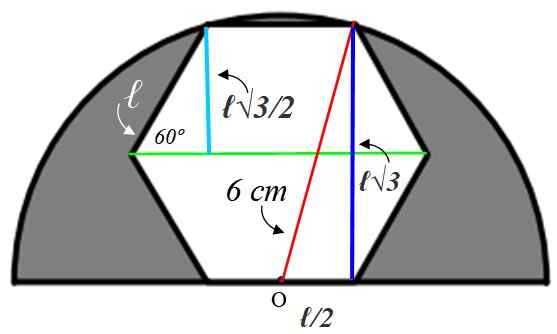
Začnimo z majhnim pravokotnim trikotnikom na levi strani, katere hipotenuza je ℓ. Notranji kot šesterokotnika je vreden:

α = [180 (n-2)]/n = α = [180 (6-2)]/6 = 120 °

Polmer, ki smo ga narisali v Bisecta Green, ta kot, zato je akutni kot majhnega trikotnika 60 °. S predloženimi informacijami je ta trikotnik razrešen in poišče svetlo modro stran, ki meri enako kot apotem:

Nasproti Cateto = a = ℓ x sin 60º = ℓ√3 / 2 cm

Ta vrednost je dvakrat temno modra noga velikega trikotnika v desno, toda iz tega trikotnika vemo, da hipotenuza meri 6 cm, ker je polmer polkroga. Preostali kateto (spodaj) je vreden ℓ/2, saj je točka ali je na sredini strani.

Ker notranji koti tega trikotnika niso znani, lahko zanj dvignemo teorem pitagore:

36 = 3 ℓ² + ℓ² / 4

(13/4) ℓ² = 36 → ℓ = √ (4 x36) /13 cm = 12 /√13 cm

S to vrednostjo se izračuna apotem:

A = ℓ√3 /2 cm = (12 /√13) x (√3 /2) cm = 6√3 /√13 cm

Pokličimo a₂ na redno območje šesterokotnika:

= 28. 8 cm²

Zasenčeno območje figure

Do₁ - Do₂ = 18π cm²  - 28.8 cm² = 27.7 cm²

Reference

1. Baldor, a. 1973. Geometrija in trigonometrija. Srednjeameriški kulturni uvodnik.
2. Uživajte v matematiki. Tesels. Okrevano od: Uživajte.com.
3. In. Do. 2003. Elementi geometrije: z vajami in geometrijo kompasa. Univerza v Medellinu.
4. Šesterokotniki v naravi. Okrevano od: Malvargamath.WordPress.com.
5. Jiménez, r. 2010. Matematika II. Geometrija in trigonometrija. Druga izdaja. Dvorana Prentice.
6. Redni poligoni. Okreval od: Mate.inženiring.USAC.Edu.Gt.
7. Wikipedija. Apotem. Okrevano od: je.Wikipedija.org.