Koncept, značilnosti, primeri, vaje Bravais Networks

The Bravais Networks So nabor štirinajstih tridimenzionalnih enot celic, v katerih atomi kristala. Te celice so sestavljene iz tridimenzionalne ureditve točk, ki tvorijo osnovno strukturo, ki se občasno ponavlja v treh prostorskih smereh.

Izvor tega poimenovanja za osnovne kristalne strukture izvira iz leta 1850, ko je Auguste Bravais pokazal, da je možnih le 14 možnih osnovnih tridimenzionalnih enot celic.

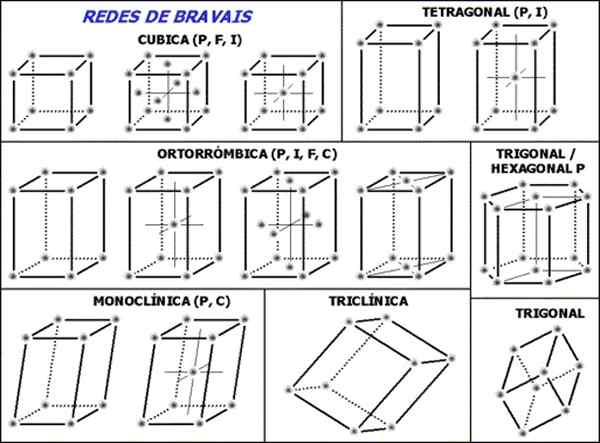
Slika 1. Bravais omrežja so nabor 14 potrebnih in dovolj enotnih celic, da opišejo katero koli kristalno strukturo. (Wikimedia Commons)

Nabor 14 Bravais Networks je razdeljen v sedem skupin ali struktur glede na geometrijo celic, teh sedem skupin je:

1- kubični

2- tetragonalni

3- ORTORROMBIC

4- trigonalno-heksagonalni

5- monoklinic

6- triklinični

7- Trigonal

Vsaka od teh strukture določa enotno celico, kar je najmanjši del, ki ohrani geometrijsko razporeditev atomov v kozarcu.

[TOC]

Značilnosti Bravais Networks

Štirinajst Bravais, kot je navedeno zgoraj, je razdeljenih v sedem skupin. Toda vsaka od teh skupin ima svoje enotne celice z značilnimi parametri, ki so:

1- omrežni parameter (a, b, c)

2- Število atomov na celico

3- Razmerje med omrežnim parametrom in atomskim radiem

4- Koordinacijska številka

5- embalažni faktor

6- Intersticijski prostori

7- s prevodi vzdolž vektorjev A, B, C Kristalna struktura se ponovi.

Kubična omrežja

Sestavljen je iz preprostega ali kubičnega kubičnega omrežja, kubično omrežje, osredotočeno na obraze ali kubično omrežje F, in kubično omrežje, osredotočeno na kubično telo ali omrežje.

Vsa kubična omrežja imajo tri Omrežni parametri ustreza X, y naslovom, z isto vrednostjo:

A = b = c

Kubično omrežje str

Priročno je poudariti, da atome predstavljajo krogle, katerih središča so v točki kubične celice P.

Vam lahko služi: umetni sateliti

V primeru kubičnega omrežja p Število atomov na celico To je 1, ker je v vsaki tolici samo osmi del atoma znotraj enotne celice, nato 8*⅛ = 1.

On Koordinacijska številka Označuje število atomov, ki so bližnji sosedje v kristalni mreži. V primeru kubičnega omrežja je koordinacijska številka 6.

Kubično omrežje i

V tej vrsti omrežja poleg atomov v točki kocke je v središču kocke atom. Tako atom številka na celico Enota v kubični mreži P je 2 atoma.

Slika 2. Kubično omrežje s telesom.

Kubično omrežje f

Kubična mreža je, da ima poleg atomov v točki atom na sredini obraza vsake kocke. On Število atomov na celico To je 4, saj ima vsak od šestih atomov obraza polovico znotraj celice, če reče 6*½ = 3 plus 8*⅛ = 1 v točki.

Slika 3. Kubično omrežje, osredotočeno na obraze.

Šesterokotna mreža

V tem primeru je enotna celica ravna šesterokotna prizma. Šesterokotne mreže imajo tri Omrežni parametri ustrezno izpolnjevanje naslednjega razmerja:

A = b ≠ c

Kot je kot med vektorjem A in B 120 °, kot je prikazano na sliki. Medtem ko sta med vektorji A in C, pa tudi med B in C, ravni koti.

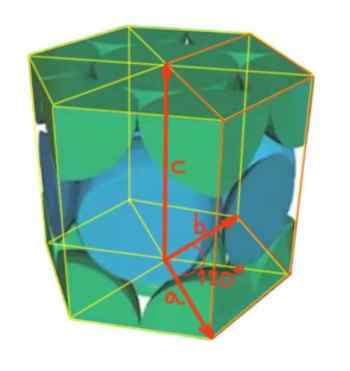Slika 4. Šesterokotna mreža.

On Število atomov na celico Izračunana bo na naslednji način:

- V vsaki od dveh baz šesterokotne prizme je 6 atomov v šestih točkah. Vsak od teh atomov zavzema ⅙ enotne celice.

- V središču vsake od dveh šesterokotnih baz je 1 atom, ki zaseda 1/2 enotne celice.

- Na 6 stranskih obrazih šesterokotne prizme so 3 atomi, od katerih vsak zaseda ⅔ enotne celice, in 3 atome, ki zasedajo vsak ⅓ volumna enotne celice.

Lahko vam služi: Slišite silo: površinske in masne sile

(6 x ⅙) x 2 + ½ x 2 + ⅔ x 3 + ⅓ x 3 = 6 

Razmerje med omrežnimi parametri A in B z atomskim polmerom R pod predpostavko, da so vsi atomi enaki radiu in so v stiku, je: 

a/r = b/r = 2

Primeri

Kovine so glavni primeri kristalnih struktur in tudi najpreprostejši, ker so na splošno sestavljene iz ene same vrste atoma. Obstajajo pa druge nemetalne spojine, ki tvorijo tudi kristalne strukture, kot so Diamond, Quartz in mnogi drugi.

- Železo

Iron ima preprosto kubično enotno celico z omrežnim parametrom ali robom A = 0,297 nm. V 1 mm je 3,48 x 10^6 enotnih celic.

- baker

Ima kubično kristalno strukturo, osredotočeno na obraze, ki jo tvorijo samo bakreni atomi.

- Dragoceni dragulji

Dragoceni dragulji so kristalne strukture v bistvu ista spojina, vendar z majhnimi deli nečistoč, ki so pogosto odgovorni za barvo njih.

Diamant

Sestavljen je samo iz ogljika in ne vsebuje nečistoč, zato nima barve. Diamant ima Kubična kristalna struktura (izometrično-heksoktaedral) in je najtežje znan material.

Kremen

Sestavljen je iz kremenčevega oksida, je običajno brezbarven ali bel. Njegova kristalna struktura je trigonalno-trapezoédrica.

Ruby 

Sestavljen je iz aluminijevega oksida s kromiranimi nečistočami, ki mu dajo značilno rdečo barvo. Oblikuje eno Šesterokotna kristalna mreža.

Sapphire 

Je tudi kristal aluminijevega oksida, vendar z nečistočami titana in železa, ki so odgovorni za njihovo modro barvo v različnih odtenkih. Kot ima Ruby Šesterokotna struktura.

Jade

Dragoceni kamen na splošno zelen, ima Monoklinična struktura In je sestavljen iz železno-magnezij-kalcijevega silikata.

Topaz 

Je brezbarven z a OrTorrambična struktura aluminijevega hidroksida-silikatnega fluorida.

Rešene vaje

Vaja 1

Poiščite razmerje med omrežnim parametrom in atomskim polmerom za kubično omrežje F.

Lahko vam služi: Teorija velikega poka: značilnosti, stopnje, dokazi, problemi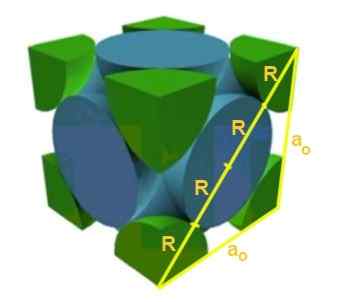

Rešitev: Najprej se domneva, da so atomi predstavljeni kot kroglice, ki so v "stiku" med seboj, kot je prikazano na sliki. Nastavljen je pravokotnik Trikotnik, v katerem je izpolnjeno:

(4 r)^2 = a^2 + a^2 = 2 a^2

Torej imate, da je odnos Edge-Radio:

A/r = 4/√2

Vaja 2

Poiščite razmerje med omrežnim parametrom in atomskim polmerom za kubično omrežje I (osredotočeno na telo).

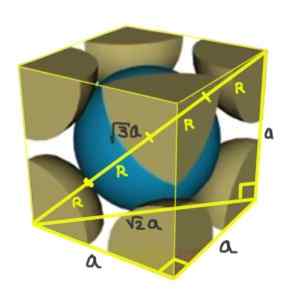
Rešitev: Atomi naj bi bili predstavljeni kot vse polmer r kroglice v "stiku" med seboj, kot je prikazano na sliki.

Dva pravokotnika sta oblikovana ena od hipotenusa √2a, druga hipotenuza √3a. Od tam se morate povezati med omrežnim parametrom in atomskim polmerom za kubično omrežje I (osredotočeno v telo) je:

A/r = 4/√3

Vaja 3

Poiščite faktor pakiranja F za enotno celico kubične strukture F (kubično osredotočeno na obraze), v kateri imajo atomi radio R in so v "stiku".

Rešitev: Faktor pakiranja F je opredeljen kot razmerje med prostornino, ki ga zasedajo atomi v enotni celici, in prostornino celice:

F = vatomi / Vcelica

Kot je prikazano zgoraj, je število atomov na enoto celice kubične mreže, osredotočene na obraze, 4, zato bo faktor pakiranja:

F = 4 [4πr^3/3] /[a^3] =…

… 4 [4πr^3/3]/[4r/√2]^3 = (√2) π/6 = 0,74

Reference

1. Akademske vire kristalne strukture. [PDF]. Pridobljeno 24. maja 2018, od: splet.iit.Edu
2. Kristali. Pridobljeno 26. maja 2018, od: Musmatco.com
3. Tiskovnice. 10.6 latičnih struktur v kristalnih trdnih snovi. Pridobljeno 26. maja 2018, od: OpenTextbc.AC
4. Ming. (30. junij 2015). Vrste kristalne strukture. Pridobljeno 26. maja 2018, od: CrystalVision-Film.com
5. Čelada, Anne Marie, ph.D. (31. januarja 2018). Vrste 
6. Kittel Charles (2013) Fizika trdne države, fizika kondenzirane snovi (8. izdaja). Wiley.
7. Khi. (2007). Kristalne strukture. Pridobljeno 26. maja 2018, od: folk.Ntnu.Ne
8. Wikipedija. Bravais Latices. Pridobljeno iz: v.Wikipedija.com.