Paralelepiped

Paralelepipedi so šeststranske geometrijske figure, kjer so nasprotja vzporedna med seboj. Primer: opeka, škatla za čevlje, vedro itd.

Kaj je vzporedni?

A paralelepiped Gre za geometrijsko telo, ki ga tvori šest obrazov, katerih glavna značilnost je, da so vsi njeni obrazi paralelogrami in tudi nasprotni obrazi vzporedni med seboj. To je pogost poliedron v našem vsakdanjem življenju, saj ga lahko najdemo v škatlah za čevlje, obliki opeke, obliki mikrovalovne pečice itd.

Ker je poliedron, paralelepiped vsebuje končni volumen in vsi njeni obrazi so ravni. Je del skupine prizm, ki so tiste poliedre, v katerih so vse njene točke vsebovane v dveh vzporednih ravninah.

Elementi paralelepiped

Obraze

So vsaka od regij, ki jih tvorijo paralelogrami, ki omejujejo vzporednico. Paralelepiped ima šest obrazov, kjer ima vsak obraz štiri sosednje obraze in nasprotno. Poleg tega je vsak obraz vzporeden s svojim nasprotnim.

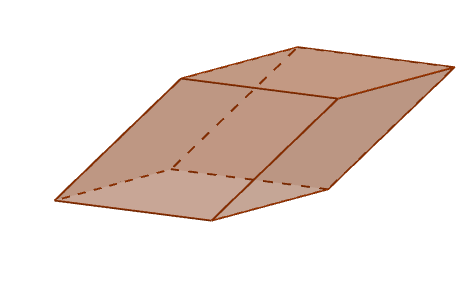Perspektiva paralelepiped

Robovi

So pogosta stran dveh obrazov. Skupno ima paralelepiped dvanajst robov.

Vertex

To je skupna točka treh obrazov, ki so sosednja dva do dva. Paralelepiped ima osem vrhov.

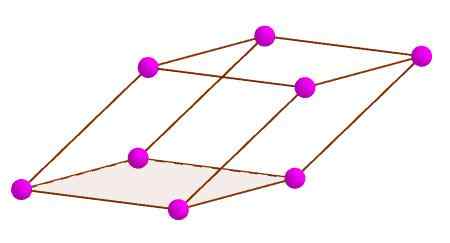Vrhovi paralelepiped

Diagonala

Glede na dva obraza vzporednima nasproti drug drugemu, lahko narišemo črto, ki sega od točke enega obraza do nasprotne točke drugega.

Ta segment je znan kot vzporedna diagonala. Vsak paralelepiped ima štiri diagonale.

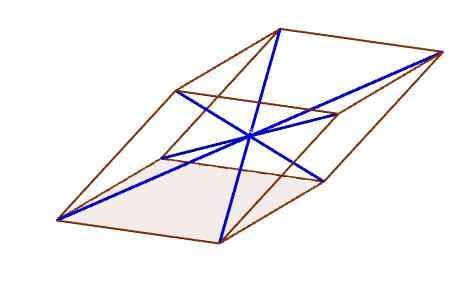Diagonale paralelepiped

Center

To je točka, na kateri se sekajo vse diagonale.

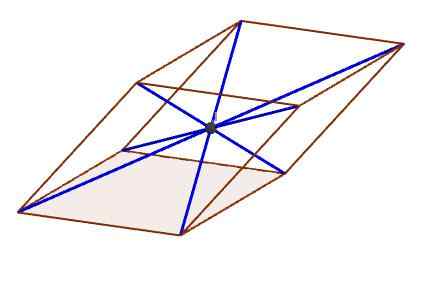Točka na sliki označuje središče, kjer se vse diagonale sekajo

Značilnosti vzporednic

Kot smo že omenili, ima to geometrijsko telo dvanajst robov, šest obrazov in osem vrhov.

V vzporednici lahko prepoznate tri sklope, ki jih tvorijo štirje robovi, ki so vzporedni med seboj. Poleg tega so robovi teh sklopov tudi v skladu z lastnostjo enake dolžine.

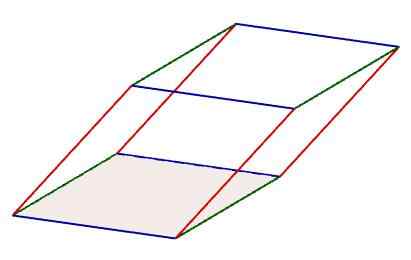Značilnosti vzporednic

Postavljena druga lastnost.

Poleg tega so paralelepipedi, ki so konveksni poliedroni, v skladu z Eulerjevim teoremom za polihedro, kar nam daje razmerje med številom obrazov, številom robov in številom točki. To razmerje je podano v obliki naslednje enačbe:

C + V = A + 2

Ta funkcija je znana kot Eulerjeva značilnost. Kjer je C število obrazov in število vrhov in število robov.

Vrste paralleparípedos

Lahko razvrstimo paralelepípedos glede na njihove obraze, po naslednjih vrstah:

Orthoedro

So paralelepípedos, kjer njihove obraze sestavljajo šest pravokotnikov. Vsak pravokotnik je pravokoten s tistimi, s katerimi si deli rob. So najpogostejši v našem vsakdanjem življenju, to je običajna oblika čevljev in opečnih škatel.

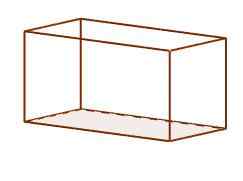Orthoedro paralelepiped

Navadna kocka ali heksaedro

To je poseben primer prejšnjega, kjer je vsak obrazi kvadrat.

Vam lahko služi: elipseNavadna kocka ali heksaedro

Kocka je tudi del geometrijskih teles, imenovanih platonske trdne snovi. Platonska trdna snov je konveksni poliedron, tako da so tako obrazi kot notranji koti enaki drug drugemu.

Romboedro

To je paralelepipe, ki ima rombo. Vsi ti rombusi so enaki drug drugemu, saj si delijo robove.

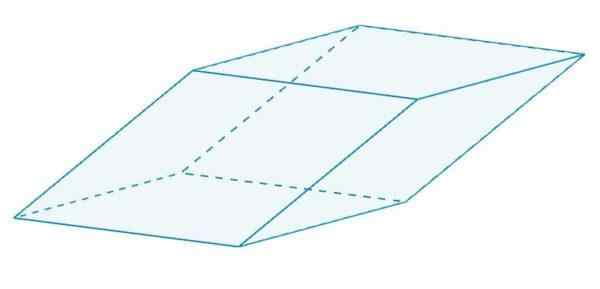Romboedro

Romboiedro

Njegovih šest obrazov je Rhomboid. Spomnimo se, da je romboid štirikotni poligon in štiri kote, ki sta enaka dva do dva. Rhomboidi so paralelogrami, ki niso niti kvadratni, niti pravokotniki, niti rombusi.

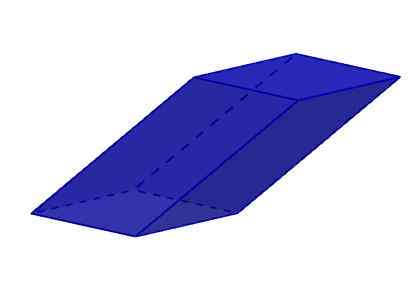Romboiedro

Po drugi strani so poševni paralelepipedi tisti, v katerih se vsaj ena višina ne ujema z njegovim robom. V tej klasifikaciji lahko vključimo Rhomboedros in Rhomboiedros.

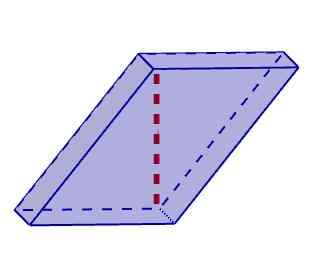Poševno paralelepiped

Diagonalni izračun

Za izračun diagonale ortoedra lahko uporabimo teorem pitagore za r³.

Spomnimo se, da ima ortoedro značilnost, da je vsaka stran pravokotna s stranicami, ki si delijo rob. Iz tega dejstva lahko sklepamo, da je vsak rob pravokoten s tistimi, ki si deli Vertex.

Za izračun dolžine diagonale ortoedra nadaljujemo na naslednji način:

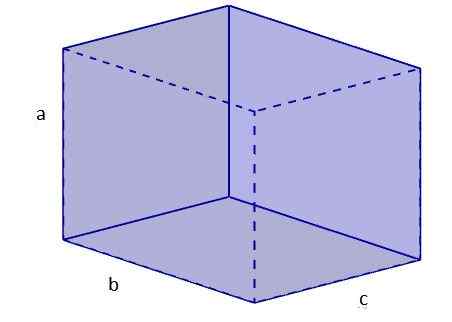
1. Izračunamo diagonalo enega od obrazov, ki jo bomo dali z bazo. Za to uporabljamo teorem Pythagoras. Poimenujmo to diagonalno d_b.

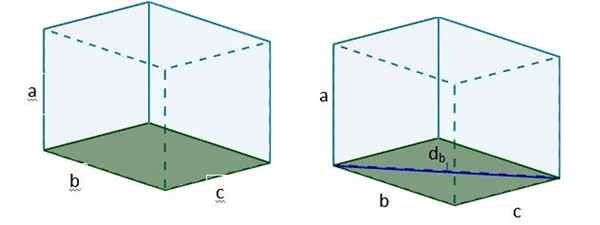
2. Nato z d_b Lahko tvorimo nov pravokotnik trikotnik, tako da je hipotenuza tega trikotnika iskana diagonala d.

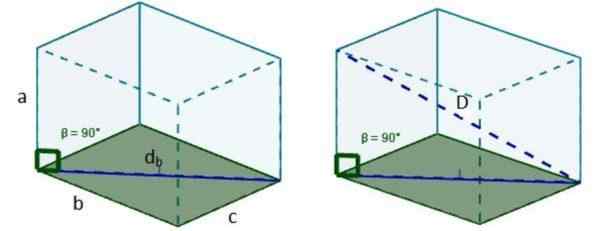
3. Ponovno uporabljamo teorem pitagore in imamo, da je dolžina te diagonale:

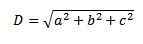
Drug način za izračun diagonale na bolj grafičen način je v vsoti prostih vektorjev.

Spomnimo se, da se dodata dva prosta vektorja A in B tako, da rep vektorja B postavita s konico vektorja A.

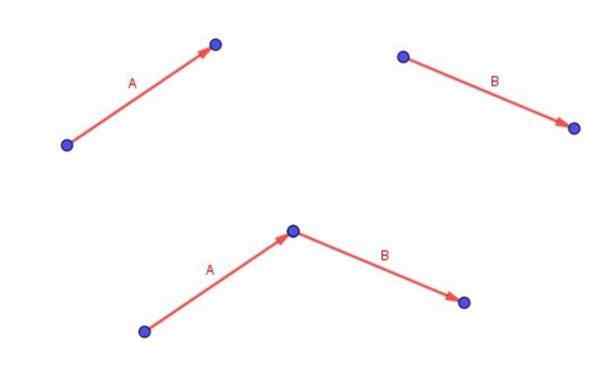
Vektor (A + B) je tisti, ki se začne v repu A in se konča na konici B.

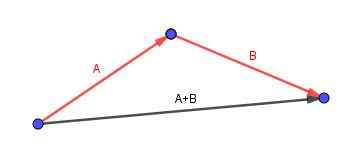
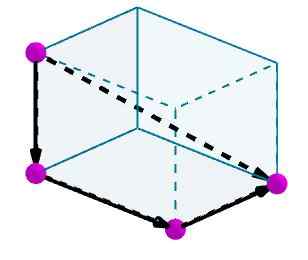
Razmislite o vzporedniku, ki ga želimo izračunati diagonalo. Robove prepoznamo z priročnimi usmerjenimi vektorji.

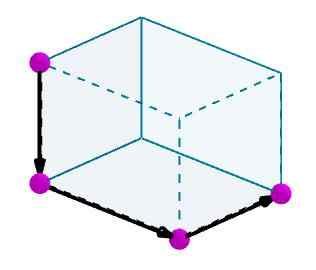
Nato dodamo te vektorje in dobljeni vektor bo diagonala paralelepiped.

Območje paralelepiped

Območje paralelepipe je podano z vsoto vsakega od območij obrazov.

Če kot osnovo določimo eno od strani,

Do_L + 2. mesto_B = Skupna površina

Kje_L Je enak vsoti območij vseh strani, ki mejijo na podlago, imenovano stransko območje in_B To je osnovno območje.

Odvisno od vrste paralelepiped, s katero delamo, lahko prepišemo omenjeno formulo.

Območje ortoedro

Daje formulo

A = 2 (AB + BC + CA).

Primer 1

Glede na naslednje ortoedro z stranicami A = 6 cm, b = 8 cm in c = 10 cm, izračunajte vzporedno in dolžino njene diagonale.

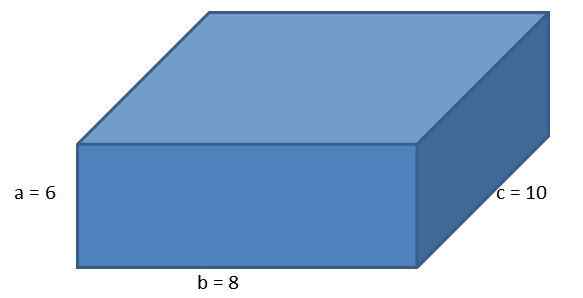
Uporaba formule za območje ortoedrov moramo

A = 2 [(6) (8) + (8) (10) + (10) (6)] = 2 [48 + 80 + 60] = 2 [188] = 376 cm².

Upoštevajte, da je kot ortoedro dolžina katere koli od njegovih štirih diagonalov enaka.

Lahko vam služi: nedoločen integral: lastnosti, aplikacije, izračun (primeri)

Z uporabo teorema pitagore za vesolje moramo

D = (6² + 8² + 10²)^1/2 = (36 + 64 + 100)^1/2 = (200)^1/2

Območje kocke

Ker ima vsak rob enako dolžino, imamo to A = B in A = C. Zamenjava v prejšnji formuli, ki jo imamo

A = 2 (aa + aa + aa) = 2 (3a²) = 6a²

A = 6a²

Primer 2

Škatla igralne konzole ima obliko kocke. Če želimo to škatlo zaviti z darilnim papirjem, koliko papirja bi porabili, če vemo, da je dolžina robov kocke 45 cm?

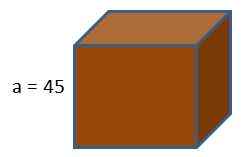
Z uporabo formule območja kocke to dobimo

A = 6 (45 cm)² = 6 (2025 cm²) = 12150 cm²

Območje romboedro

Ker so vsi njeni obrazi enaki, je dovolj, da izračunamo območje enega od njih in ga pomnožite s šestimi.

Imamo, da lahko območje rombusa izračunamo z njenimi diagonali z naslednjo formulo

Do_R = (Dd)/2

S to formulo sledi, da je skupna površina romboedro

Do_T = 6 (dd)/2 = 3dd.

Primer 3

Obrazi naslednjega romboedro tvori romb, katerega diagonala je d = 7 cm in d = 4 cm. Vaše območje bo

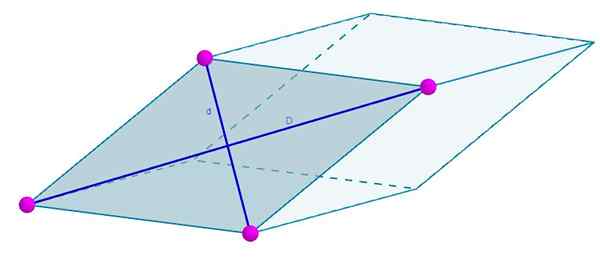
A = 3 (7 cm) (4 cm) = 84 cm².

Območje romboiedro

Za izračun območja romboiedro moramo izračunati območje romboidov, ki ga sestavljajo. Ker paralelepipede izpolnjujejo lastnost, da imajo nasprotne strani isto območje, lahko stranice povežemo v treh vrstnikih.

Na ta način bomo imeli, da bo vaše območje

Do_T = 2b₁h₁ + 2B₂h₂ + 2B₃h₃

Kjer b_Yo so baze, povezane s stranicami in h_Yo njegova relativna višina, ki ustreza omenjenim bazam.

Primer 4

Razmislite o naslednjem vzporednici,

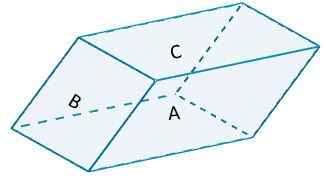
Kjer sta a in strani A '(njihova nasprotna stran) temeljita b = 10 in na višino h = 6. Označeno območje bo imelo vrednost

Do₁ = 2 (10) (6) = 120

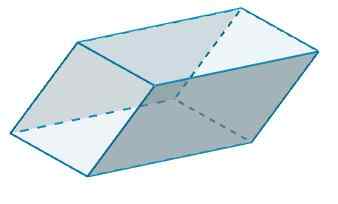
B in B 'imata B = 4 in H = 6

Do₂ = 2 (4) (6) = 48

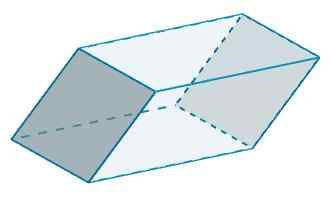
In c in c 'imata tudi b = 10 in h = 5

Do₃ = 2 (10) (5) = 100

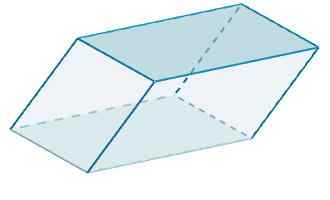
Končno je območje Rhomboiedro

A = 120 + 48 + 100 = 268.

Prostornina paralelepiped

Formula, ki nam daje količino vzporednic, je produkt območja enega od njegovih obrazov zaradi višine, ki ustreza omenjenemu obrazu.

V = a_Ch_C

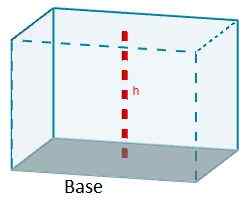
Glede na vrsto paralelepiped lahko to formulo poenostavimo.

Tako imamo na primer, da bi glasnost ortoedra dala

V = ABC.

Kjer a, b in c predstavljajo dolžino orthoedrovih robov.

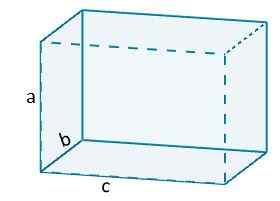
In v posebnem primeru je kocka

V = a³

Primer 1

Obstajajo trije različni modeli za škatle za piškote in želite.

Prva je kocka, katere rob ima dolžino a = 10 cm.

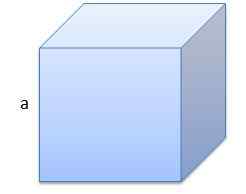
Njegova glasnost bo v = 1000 cm³

Drugi je b = 17 cm, c = 5 cm, d = 9 cm.

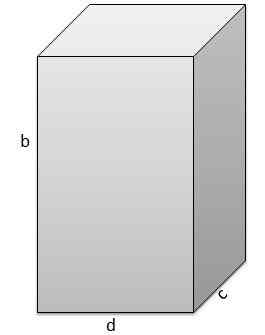
In zato je njegova glasnost v = 765 cm³

In tretji ima E = 9 cm, f = 9 cm in g = 13 cm.

In njegova glasnost je v = 1053 cm³

Vam lahko služi: vrste kotov, značilnosti in primerov

Zato je škatla z največjo glasnostjo tretja.

Druga metoda za pridobitev količine paralelepiped je, da se zateče k vektorski algebri. Zlasti trojni skalarni izdelek.

Ena od geometrijskih interpretacij trojnega skalarnega izdelka je glasnost paralelepiped, katerih robovi so trije vektorji, ki imajo isto točko kot izhodišče.

Na ta način, če imamo paralelepipe in želimo vedeti, kakšen je njen glasnost, je dovolj, da ga predstavljamo v koordinatnem sistemu v R³ sovpada eno od svojih točk z izvorom.

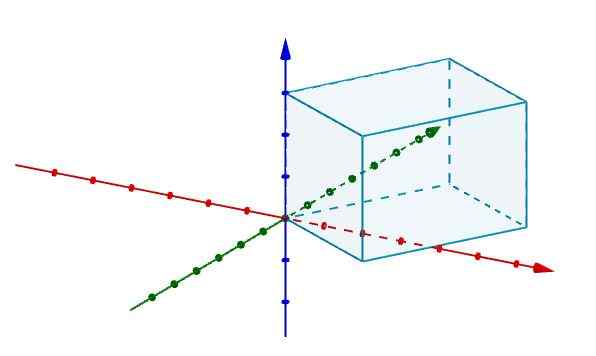
Nato predstavljamo robove, ki se pri izvoru strinjajo z vektorji, kot je prikazano na sliki.

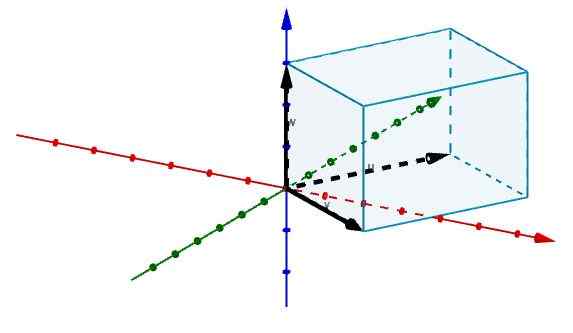
In na ta način imamo, da količino omenjenega paralelepiped daje

V = | AXB ∙ C |

Ali enakovreden, prostornina je determinanta matrice 3 × 3, ki jo tvorijo komponente ročnih vektorjev.

Primer 2

Z zastopanjem naslednjega paralelepiped v r³ Vidimo, da so vektorji, ki ga določajo, naslednje

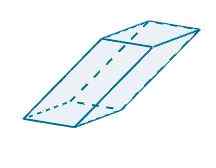
u = (-1, -3,0), v = (5, 0, 0) in w = (-0.25, -4, 4)

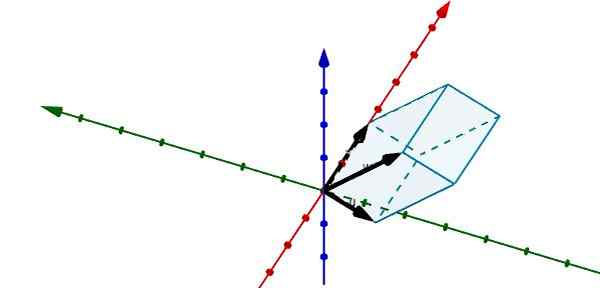
Z uporabo trojnega skalarnega izdelka, ki ga imamo

V = | (UXV) ∙ W |

Uxv = (-1, -3,0) x (5, 0, 0) = (0,0, -15)

(UXV) ∙ W = (0,0, 15) ∙ (-0.25, -4, 4) = 0 + 0 + 4 ( - 15) = - 60

To zaključuje, da je v = 60

Razmislite o tem, da je naslednje vzporedno v r³ katerih robovi določajo vektorji

A = (2, 5, 0), b = (6, 1, 0) in c = (3, 4, 4)

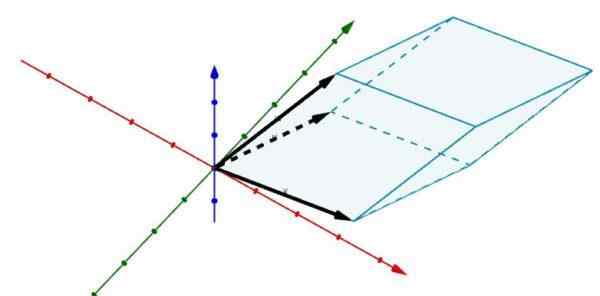
Uporaba determinantov nam to daje

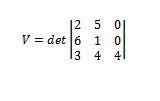
Tako imamo, da je obseg omenjenega paralelepiped 112.

Oba sta enakovredna načina izračuna prostornine.

Popolno paralelepiped

Znana je kot Eulerjeva opeka (ali Euler Block) v ortoedro, ki izpolnjuje lastnost, da sta dolžina robov in dolžina diagonalov vsakega obraza celotna številka.

Medtem ko Euler ni bil prvi znanstvenik, ki je preučil ortoederje, ki se srečujejo s to lastnino, je našel zanimive rezultate o njih.

Najmanjšo Eulerjevo opeko je odkril Paul Halcke (1662-1731), dolžine njegovih robov pa so A = 44, B = 117 in C = 240.

Odprta težava v teoriji številk je naslednji:

Ali obstajajo popolni ortoederji?

Trenutno to vprašanje še vedno nima odgovora, saj ni bilo mogoče dokazati, da ni teles, a nikogar ni bilo mogoče najti.

Do zdaj je bilo dokazano, da to počne popolna paralelepiped. Prva, ki jo je mogoče odkriti, ima dolžino svojih robov vrednosti 103, 106 in 271.

Reference

1. Fant, r. (1981). Nerešeni problemi v teoriji številk. Springer.
2. Landaverde, f. d. (1997). Geometrija. Napredek.
3. Leithold, l. (1992). Izračun z analitično geometrijo. Harla, s.Do.
4. Rendon, a. (2004). Tehnična risba: zvezek z dejavnostjo 3 2. baccalaureate. Tebar.
5. Resnick, r., Halliday, d., & Krane, k. (2001). Vol fizika. 1. Mehika: Continental.