Koncept linearnih valov, značilnosti, primeri

The Linearni valovi To so tisti, v katerih je uporabno načelo superpozicije, to je, da lahko valovna oblika in njeni vesoljski in čas evolucije dosežemo kot vsota osnovnih rešitev, na primer harmoničnega tipa. Vsi valovi ne ustrezajo načelu superpozicije, ki ga ne upoštevajo nelinealni valovi.

"Linearno" poimenovanje izhaja iz dejstva, da linearni valovi vedno izpolnjujejo diferencialno enačbo v delnih derivatih, v katerih se vsi izrazi, ki vključujejo odvisno spremenljivko ali njene izpeljane, dvignejo na prvo moč.

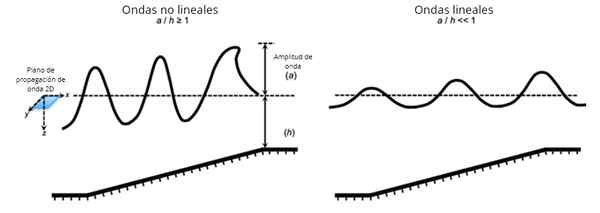
Valovi, ki jih vidimo v daljavi, so linearni valovi, vendar so prestrašeni valovi ospredja nelinealni. Vir: Pixabay.

Po drugi strani pa nelinealni valovi izpolnjujejo enačbe valov, ki imajo kvadratne ali višje stopnje v odvisni spremenljivki ali v svojih derivatih.

Včasih je zmeden na linearne valove z vzdolžnimi valovi, ki so tisti, v katerih se vibracije pojavljajo v isti smeri širjenja, kot so zvočni valovi.

Toda vzdolžni valovi, pa tudi prečni, so lahko linearni ali nelinearni, odvisno od drugih dejavnikov.

Na splošno se zgodi, da je, ko je začetna motnja majhne amplitude, enačba, ki opisuje širjenje vala, linearnega tipa ali pa jo lahko določijo določeni pristopi, čeprav ni vedno tako.

[TOC]

Diferencialna enačba v linearnih valovih

V linearnem mediju lahko omejeno valovno obliko v prostoru in času predstavljamo vsota sinusov ali kosinusnih valovnih funkcij različnih frekvenc in valovnih dolžin prek serije Fourier. 

Linearni valovi imajo vedno diferencialno enačbo povezanega linearnega tipa, katere rešitev predstavlja napoved, kakšna bo motnja v zadnjih trenutkih začetne motnje, ki se nahaja v začetnem začetnem trenutku.

Klasična enačba linearnega vala v eni sami prostorski dimenziji, katere rešitve so linearni valovi, so:

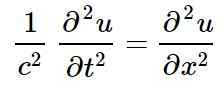
V prejšnji enačbi ali predstavlja motnjo določene fizične količine v položaju x In trenutno t, to pomeni ali Je funkcija x in t:

Lahko vam služi: kaj so koplanares vektorji? (Z rešenimi vajami)

u = u (x, t)

Na primer, če je zvočni val v zraku, ali Lahko predstavlja spreminjanje tlaka glede na njegovo vrednost, ne da bi moteno.

V primeru elektromagnetnega vala ali predstavlja električno polje ali magnetno polje, ki niha pravokotno na smeri širjenja.

V primeru napete vrvi, ali Predstavlja križni premik glede na ravnovesje ravnotežja vrvi, kot je prikazano na naslednji sliki:

Valovna oblika v danem trenutku, v primeru linearnih valov je ta oblika prekrivanje sinusoidnih valov različnih frekvenc in valovnih dolžin. Vir: f. Zapata.

Rešitve diferencialnih enačb

Če imate dve ali več rešitev linearne diferencialne enačbe, bo vsaka rešitev, pomnožena s konstanto. 

Za razliko od nelinearnih enačb, valovične enačbe priznavajo harmonične rešitve tipa: 

ali₁= A⋅sen (k⋅x - ω⋅t) in ali₂= A⋅sen (k⋅x + ω⋅t) 

To je mogoče preveriti s preprosto nadomeščanjem v enačbi linearnega vala.

Prva rešitev predstavlja progresivni val, ki napreduje v desno, drugo pa na levi C = ω/k.

Harmonske rešitve so značilne za enačbe linearnih valov.

Po drugi strani je linearna kombinacija dveh harmoničnih raztopin tudi rešitev za enačbo linearnega vala, na primer:

u = a₁ cos (k₁⋅x - ω₁⋅t) + a₂ greh (k₂⋅x - ω₂⋅t) je rešitev.

Najpomembnejša značilnost linearnih valov je, da lahko katero koli obliko vala, pa čeprav zapletena, dobimo z vsoto preprostih harmoničnih valov v dojki in kosinusu:

u (x, t) = a₀ + ∑_n Do_n cos (k_n⋅x - ω_n⋅t) + ∑_m B_m greh (k_m⋅x - ω_m⋅t).

Disperzivni in ne -desperzivni linearni valovi

V klasični enačbi linearnega vala, c predstavlja hitrost širjenja impulza.

Neisperzivni valovi

V primerih, kjer c To je konstantna vrednost, na primer elektromagnetni valovi v praznini, nato impulz v začetnem trenutku t = 0 Oblika f (x) Širi se po:

u (x, t) = f (x - c⋅t)

Ne da bi trpeli popačenje. Ko se to zgodi, se reče, da medij ni zasnovan.

Disperzivni valovi

Vendar pa je v disperzivnih medijih hitrost širjenja C lahko odvisna od valovne dolžine λ, torej: C = C (λ).

Vam lahko služi: enačba kontinuitete

Elektromagnetni valovi so disperzivni pri potovanju skozi materialni medij. Tudi površinski valovi vode potujejo z različno hitrostjo glede na globino vode.

Hitrost, s katero se širi harmonični val A⋅sen (k⋅x - ω⋅t) je Ω/k = c in fazna hitrost se imenuje. Če je medij disperziven, potem c To je funkcija valovne številke k: C = C (k), kje k Je povezan z valovno dolžino s pomočjo K = 2π/λ.

Disperzijske odnose

Razmerje med frekvenco in valovno dolžino se imenuje Razpršeno razmerje, ki se izraža v kotni frekvenci Ω in valovno številko k je: Ω = C (k) ⋅K.

Nekatere značilnosti disperzijskih razmerij linearnih valov so naslednje:

V valovih, v katerih je valovna dolžina (razdalja med grebeni) veliko večja od globine H, Toda da je njegova širina veliko manjša od globine, je razpršeno razmerje:

Ω = √ (gh) ⋅K

Od tam je sklenjeno, da se širijo s konstantno hitrostjo √ (gh) (ne -disperzivna polovica).

Toda valovi v zelo globokih vodah so disperzivni, saj je njihovo disperzijsko razmerje:

ω = √ (g/k) ⋅K

To pomeni, da fazna hitrost Ω/k Je spremenljiva in je odvisna od števila valov in s tem valovne dolžine vala.

Skupinska hitrost

Če se dve harmonični linearni valovi prekrivata, vendar napredujeta z različnimi hitrostmi, se skupina skupin (torej valovitega paketa) ne ujema s fazno hitrostjo.

Skupinska hitrost v_g Opredeljen je kot frekvenčni derivat glede na število valov v razmerju disperzije: v_g = Ω '(k).

Naslednja slika prikazuje prekrivanje ali vsoto dveh harmoničnih valov ali₁= A⋅sen (k₁⋅x - ω₁⋅t) in ali₂= A⋅sen (k₂⋅x - ω₂⋅t) to potuje z različnimi hitrostmi v₁= Ω₁/k₁ in v₂= Ω₂/k₂. Upoštevajte, kako se hitrost skupine razlikuje od fazne hitrosti, v tem primeru je skupina skupine ∆ω/∆K.

Lahko vam služi: magnetne lastnosti materialov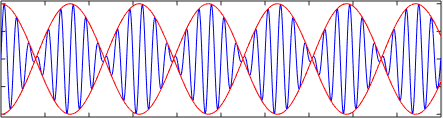Linearni (modri) val v disperzivnem mediju. Rdeča krivulja je dodana, da poudari, da se hitrost skupine razlikuje od hitrosti širjenja

Odvisno od disperzijskega razmerja imata fazna hitrost in hitrost skupine v nasprotnih smereh celo nasprotna smeri.

Primeri linearnih valov

Elektromagnetni valovi

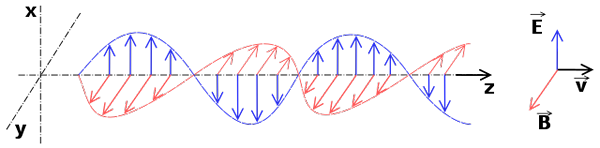Elektromagnetni valovi, ki sestavljajo elektromagnetno sevanje

Elektromagnetni valovi so linearni valovi. Njegova valovna enačba je razvidna iz enačb elektromagnetizma (Maxwell enačbe), ki so tudi linearne.

Schrödingerjeva enačba

Enačba opisuje dinamiko delcev na atomskem lestvici, kjer so valovilne značilnosti pomembne, na primer primer elektronov v atomu.

Potem je "elektronski val" ali valovna funkcija, kot se imenuje, linearni val.

Valovi v globoki vodi

Linearni valovi so tudi tisti, pri katerih je amplituda veliko nižja od valovne dolžine in valovne dolžine, veliko večji od globine. Valovi v globoki vodi sledijo linearni teoriji (znani kot Airyjeva valovita teorija).

Vendar je val, ki se približuje obali in tvori značilni greben, ki je valjan (in da deskarji ljubi) nelinearni val.

Zvok

Ker je zvok majhna motnja atmosferskega tlaka, se šteje za linearni val. Vendar so udarni val eksplozije ali valovnega fronta nadzvočne ravnine tipični primeri nelinearnih valov.

Valovi na napeti vrvi

Valovi, ki se širijo skozi napeto vrv.

Linearni valovi na strunah se odražajo na njihovih koncih in prekrivanju, kar povzroča stacionarne valove ali vibracijske načine, ki dajejo harmonične in podzemne tone, značilne za godalne instrumente.

Reference

1. Griffiths G in Schiesser W. Linearni in nelinearni valovi. Okrevano od: sholarpedia.org.
2. Whitham g.B. (1999) "Linearni in nelinearni valovi". Wiley. 
3. Wikipedija. Nelinearni valovi. Okrevano od: je.Wikipedija.com
4. Wikipedija. Nelinearna akustična. Pridobljeno iz: v.Wikipedija.com
5. Wikipedija. Valovi. Pridobljeno iz: v.Wikipedija.com
6. Wikivav. Nelinearni valovi. Okrevano od: wikivav.org