Lastnosti serije Fibonacci, naravni odnosi, aplikacije

The O serija Fibonacci nasledstvo je zaporedje števil, ki jih dobimo z začetkom z 0 in 1, nadaljuje z vsoto od njih: 0 + 1 = 1, nato vsota prejšnjih dveh: 1 + 1 = 2 in tako naprej.

Po tem postopku dobimo drugi izrazi, poglejmo: 2 + 1 = 3, 3 + 2 = 5, 5 + 3 = 8, 8 +5 = 13…

Prve številke serije Fibonacci

Postopek se ponovi tolikokrat, kot želite. Na ta način je v obliki Fibonaccijevega nasledstva: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 .. Številke, ki jih imenujejo Fibonaccijeve številke.

[TOC]

Zgodovina

Nasledek Fibonaccija se imenuje italijanski matematik, ki je živel v srednjem veku: Leonardo de Pisa, znan tudi kot Fibonacci (1175-1250). 

Leonardo de Pisa

Leonardo je otroštvo preživel v Severni Afriki in potoval po Sredozemlju, kjer je poznal indo -arabski sistem za oštevilčenje in bil navdušen nad njim. Verjetno so ga Leonardovi arabski učitelji naučili o nasledstvu, ki so ga že poznali hindujski matematiki.

Kasneje, ko se je vrnil v Pisa Fibonacci, je napisal knjigo z naslovom Liber Abaci (Knjiga Abakusa), kjer je poleg poudarjanja prednosti indoarabskih številk pred rimskim oštevilčenjem in uvajanjem 0 sprožil težavo glede reprodukcije zajcev.

In rešitev tega problema je natančno število nasledstva Fibonacci.

Leonardo de Pisa ni prejel ustvarjanja nasledstva; Omenil ga je le v svoji knjigi kot radovednost, ki je pritegnila pozornost številnih učenjakov, ki so mu sledili. Med njimi je bil francoski matematik devetnajstega stoletja Edouard Lucas, ki jo je med preučevanjem nasledstva krstila z imenom srednjeveškega žajblja.

Problem fibonaccijevih zajcev

Težava pravi: za vedno živi nekaj zajcev, ki je v dveh mesecih rodovitna. Ko je zrelost dosežena, imajo vsak mesec nekaj dojenčkov različnih seksa, ki trajajo tudi dva meseca za razmnoževanje in imajo mesečno par zajcev.

Vam lahko služi: de Morgan zakoni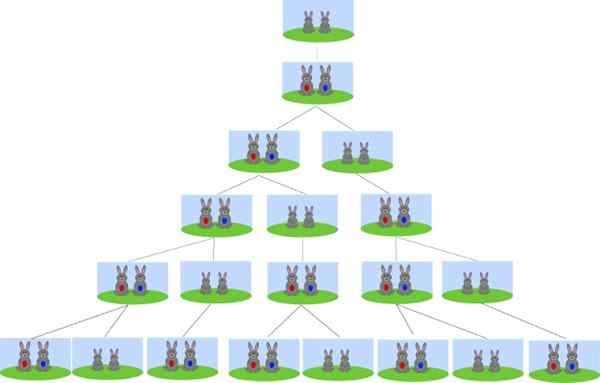Izvor Fibonaccijevega nasledstva je v problemu razmnoževanja zajcev. Vir: Wikimedia Commons.

Začenši z nekaj novorojenčki, koliko parov zajcev bo čez en mesec? Koliko parov zajcev bo po 2, 3 in 4 mesecih? In koliko jih bo po 6 mesecih?

Odgovor je v številkah Fibonacci. Po 1 mesecu je 1 par zajcev, originalni par, saj se razmnožujejo šele po 2 mesecih.

Po 2 mesecih sta dva para zajcev: originalni par in njihovo prvo leglo.

Pri 3 mesecih bomo imeli 3 pare, vključno z originalnim parom, njihovo prvo leglo in novo.

Ko bomo dosegli 4. mesec, bomo imeli originalni par, prvo leglo, ki ima svoje prve otroke, leglo tretjega meseca in novo leglo. Skupaj 5 parov zajcev.

Toda to je število Fibonaccijevih zaporedja, zato bo po 6 mesecih 13 parov zajcev, saj se vsak mesec dodajo pari prejšnjih dveh mesecev.

Lastnosti serije Fibonacci

Tu je nekaj zanimivih lastnosti nasledstva Fibonacci.

Lastnina 1

Rekurzivna formula za iskanje pogojev nasledstva je:

do_N+1 = a_n + do_N-1  Za n večje ali enake 2.

Kjer je n = 2, 3, 4,… to je, da bi našli sedmi izraz a₇, Naredimo n = 6, tako da je 6+1 = 7. Pogoje moramo vedeti₅  že₆, seznama, ki se pojavi v uvodu v₅ = 5 in a₆ = 8, torej do₇ = 5+8 = 13.

Lastnina 2

Če dva izraza, ki jih želita najti, nista znana, potem lahko uporabimo naslednjo formulo:

Lahko vam služi: tesseldos: značilne, vrste (redne, nepravilne), primeri

Lastnina 3

Številke a_n že_N+1 so  Coprmos, to pomeni, da so bratranci med seboj, kar pomeni, da nimajo skupnih skupnih dejavnikov.

Lastnina 4

Zelo zanimiva lastnost je količina med pogoji_2N že_n, ki je vreden 1, ko je n = 1. To pomeni:

do₂ / do₁ = 1

Z lahkoto ga lahko preverimo s seznamom Fibonaccijevih številk.

Po drugi strani, če je n ≠ 1, potem je količnik:

do_2N / do_n = a_n  + 2. mesto_N-1

Na primer, če je n = 3, potem a _2N = a₆ = 8 in₃ = 2. No, potem:

8/2 = 2 + 2. do₂ = 2 + 2. 1

Dejansko: 8/2 = 4 in 2 + (2.1) = 4. Preveriti je mogoče, da je izpolnjena katera koli N vrednost.

Lastnina 5

Razmerje r_n = a_N+1 / do_{n ,} Ko n postane odličen, se zbliža v Zlati razlog tudi Aurea delež, Iracionalna številka, ki se pogosto pojavlja v naravi, daje:

Naravni odnosi nasledstva Fibonacci

Fibonaccijevo nasledstvo v rastlinah

Manifestacije nasledstva Fibonaccije so v rastlinskem kraljestvu

Podružnice nekaterih dreves vsako leto izidejo v skladu z naslednikom Fibonaccija. Prvo leto deblo raste, ne da bi vrgel nobeno vejo, po enem letu ustvari eno in tako v vsakem letu. Vsaka veja lahko po enem letu vrže še enega novega, tako kot se zajci razmnožujejo.

Center za sončnične rože vsebuje semena, razporejena v logaritmičnih spiralnih tramovih, v obeh pomenu, katerih količine ustrezajo dvema zaporednima številkama Fibonacci.

Številke Fibonacci so prisotne v številu cvetnih listov sončnic in margarita, pa tudi v številnih vzorcih, v katerih imajo rastline svoje liste.

Vam lahko služi: ordinalna spremenljivka

Strokovnjaki pravijo, da na ta način rastline optimizirajo prostor za liste in rože, da imajo optimalno rast.

Z osrednjo točko kot izhodišče te strukture rastejo in prejemajo sončno svetlobo, zato morajo novi listi in cvetni listi pokriti čim manj tiste, ki so se najprej pojavili. In najboljši način za dosego tega je sprejeti vzorec rasti v smislu zaporedja Fibonacci.

Fibonaccijevo nasledstvo pri živalih

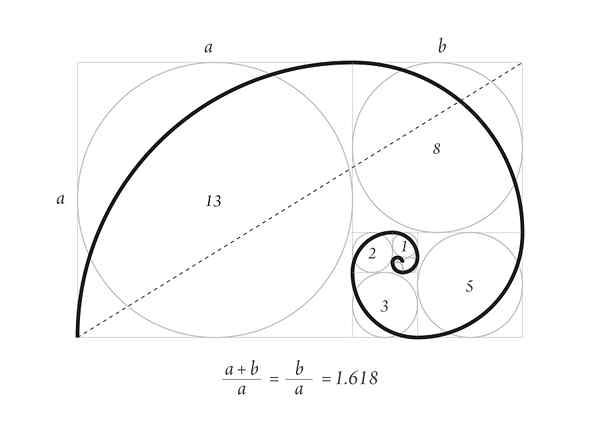Durerova spirala s prvim številom nasledstva Fibonaccija

Trpežna spirala nadrejene podobe je del rastnega vzorca školjk pri morskih živalih in rogov nekaterih prežvekovalcev.

Začnite z dvema kvadratma 1, enega na vrhu drugega, nato kvadrat strani 2 poleg njega, ki sestavlja pravokotnik strani 3, katere stranice imajo zlati delež.

Spodaj je kvadrat strani 3 in na levi kvadrat strani 5. Zgoraj je kvadrat strani 8 in desno kvadrat strani 13. To je prva številka nasledstva.

Končno se spirala nariše z dotikom točk vogalov kvadratov, kot je razvidno iz slike.

Prijave

Nasledek Fibonaccija se uporablja na različnih področjih:

-V umetnosti se zlati delež, povezan z nasledstva Fibonaccija, pojavlja pri ljudeh in stvareh, ki jih predstavljajo veliki umetniki, kot so Leonardo Da Vinci, Miguel Ángel in Alberto Durero.

-Delež partnerja v Atenah se odziva tudi na številko zlata.

-V skladbah Mozarta, Beethoven, Schubert in Debussy.

-Za oblikovanje predmetov, katerih deleži so harmonični za človeške oči, kot so kreditne kartice, zabojnike, zastave.

-Na borzi se uporablja za napovedovanje, kakšne cene se spreminjajo v njen trend.

Reference

1. Fibonacci nasledstvo. Okrevano od: blogeducastur.je.
2. Stewart, J. 2007. Prekalenkulacija. 5. Izdaja. Cengage učenje.
3. Vargas, m. Aplikacije za nasledstvo Fibonacci. Okreval od: matesUp.Cl.
4. Wikipedija. Številka fibonaccije. Pridobljeno iz: v.Wikipedija.org.