Lastnosti namišljenih številk, aplikacije, primeri

The Namišljene številke So tisti, ki dajejo rešitev za enačbo, v kateri je neznano, kvadratno povišano, enake resničnemu negativnemu številu. Namišljena enota je I = √ (-1).

V enačbi: z²= - a, z To je namišljena številka, ki je izražena na naslednji način:

 Z = √ (-a) = i√ (a)

Biti do Pozitivno resnično število. Ja A = 1, tako z = i, kje Yo je namišljena enota.

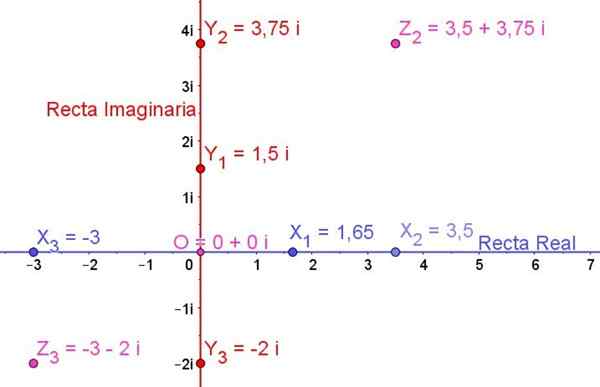Slika 1. Kompleksna ravnina, ki prikazuje nekaj resničnih številk, nekaj namišljenih in nekaj zapletenih številk. Vir: f. Zapata.

Na splošno je namišljena številka Z vedno izražena v obliki: 

z = y⋅i

Kje in Je resnično število in Yo je namišljena enota.

Kot tudi realne številke so predstavljene na vrsti, imenovani Res naravnost, Analogno namišljene številke so predstavljene na Namišljeno naravnost.

The Namišljeno naravnost Je vedno pravokotna (oblika 90 °) Res naravnost in obe vrstici določata kartezijansko ravnino, imenovano Zapletena ravnina.

Slika 1 prikazuje kompleksno ravnino in nekaj resničnih števil, na njej je predstavljenih nekaj namišljenih števil in tudi nekaj zapletenih števil:

X₁, X₂, X₃ So resnične številke

In₁, In₂, In₃ So namišljene številke

Z₂ in z₃ So zapletene številke

Številka ali je resnična ničla in je tudi namišljena ničla, tako da je izvor ali je ničelni kompleks, izražen z:

0 + 0i 

[TOC]

Lastnosti

Nabor namišljenih številk označuje:

I = …, -3i,…, -2i,… .,-Yo, .. .,0i, .. .,Yo, .. .,2i, .. .,3i,…

In nekatere operacije o tem numeričnem nizu je mogoče določiti. Namišljena številka ni vedno pridobljena iz teh operacij, zato jih bomo videli z malo več podrobnosti:

Vsota in odštevanje namišljenih

Namišljene številke lahko dodajajo in odštejejo drug od drugega, zato bo prišlo do novega namišljenega števila. Na primer:

Vam lahko služi: relativni bratranci: kaj so, razlaga, primeri

 3i + 2i = 5i

4i - 7i = -3i

Namišljeni izdelek

Ko je izdelan produkt namišljene številke z drugo, je rezultat resnično število. Naredimo naslednjo operacijo, da preverimo:

2i x 3i = 6 x i² = 6 x (√ (-1))² = 6 x (-1) = -6.

In kot vidimo, je -6 resnično število, čeprav je bilo pridobljeno z množenjem dveh čistih namišljenih številk.

Produkt resnične številke za drugo namišljeno

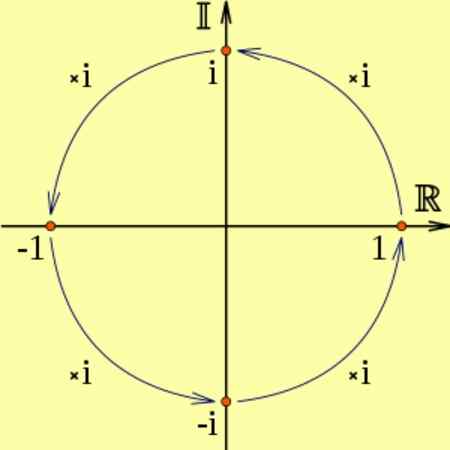
Če resnično število pomnoži I, bo rezultat namišljena številka, ki ustreza vrtenju 90 stopinj.

In je to² ustreza dvema zaporednimi rotacijami 90 stopinj, kar je enakovredno množitvi za -1, to je jaz² = -1. To je razvidno iz naslednjega diagrama:

Slika 2. Množenje namišljene enote in ustreza rotaciji 90 °. Vir: Wikimedia Commons.

Na primer:

-3 x 5i = -15i

-3 x i = -3i.

Potenciranje namišljenega

Potenciacijo namišljenega števila na celoten eksponent je mogoče določiti:

Yo¹ = i

Yo² = i x i = √ (-1) x √ (-1) = -1

Yo³ = i x i² = -I

Yo⁴ = i² x i² = -1 x -1 = 1

Yo⁵ = i x i⁴ = i

Na splošno morate Yoⁿ = i^(n mod 4), kje Mod To je ostanek delitve med n in 4.

Prav tako je mogoče izvesti potencial negativnih celih števil:

Yo^-1 = 1 / i¹ = i / (i x i¹) = I / (i²) = I / (-1) = -i

Yo-² = 1 / i² = 1/ (-1) = -1

Yo-³= 1 / i³ = 1 / (-i) = (-1) / i = -1 x i^-1 = (-1) x (-i) = i

Na splošno je namišljena številka B⋅i, povišana za moč n,::

(B⋅i) iⁿ = bⁿ Yoⁿ = bⁿ i^(n mod 4)

Nekaj ​​primerov je naslednje:

(5 i)¹² = 5¹² Yo¹² = 5¹² Yo⁰ = 5¹² x 1 = 244140625

(5 i)^enajst = 5^enajst Yo^enajst = 5^enajst Yo³ = 5^enajst x (-i) = -48828125

(-2 i)¹⁰ = -2¹⁰ Yo¹⁰ = 2¹⁰ Yo² = 1024 x (-1) = -1024

Vsota resničnega števila in ene namišljene

Ko se z namišljenim doda resnično število, rezultat ni niti resničen niti namišljen, je nova vrsta številke, ki se imenuje Zapletena številka.

Na primer, če je x = 3,5 in y = 3,75i, potem je rezultat zapletena številka:

Vam lahko služi: minimalni kvadratki

Z = x + y = 3,5 + 3,75 i

Upoštevajte, da resničnih in namišljenih delov ni mogoče razvrstiti v vsoto, zato bo zapletena številka vedno imela resničen del in drug namišljeni del.

Ta operacija razširja niz realnih številk na najširše kompleksne številke.

Prijave

Ime namišljenih številk je francoski matematik René Descartes (1596-1650) predlagal kot posmeh ali nesoglasje s predlogom, ki ga je podal italijanski matematik Raffaelle Century Bomballi.

Drugi veliki matematiki, kot sta Euler in Leibniz, so v tem nesoglasju dodelili Descartes in kot namišljene številke imenovali kot namišljene številke Številke dvoživk, o katerih so razpravljali med bitjem in nič.

Ime namišljenih številk se danes vzdržuje, vendar je njen obstoj in pomen zelo resničen in občutljiv, saj se naravno pojavljata na številnih področjih fizike, kot so:

-Teorija relativnosti.

-V elektromagnetizmu.

-Kvantna mehanika.

Vadite z namišljenimi številkami

- Vaja 1

Poiščite rešitve naslednje enačbe:

z² + 16 = 0

Rešitev

z² = -16

Vzeti kvadratni koren pri obeh članih:

√ (z² ) = √ (-16)

± z = √ (-1 x 16) = √ (-1) √ (16) = i x 4 = 4i

Z drugimi besedami, rešitve izvirne enačbe so:

z = +4i ali z = -4i.

- Vaja 2

Poiščite rezultat dviga namišljene enote na moč 5 minus odštevanje namišljene enote, dvignjene na moč -5.

Rešitev

Yo⁵ - Yo-⁵ = i⁵ - 1/i⁵ = i - 1/i = i - (i)/(i x i) = i - i/( - 1) = i + i = 2i

- Vaja 3

Poiščite rezultat naslednje operacije:

(3i)³ + 9i 

Rešitev

3³ Yo³ - 9 = 9 (-i) + 9i = -9i + 9i = 0i

- Vaja 4

Poiščite rešitve naslednje kvadratne enačbe:

Vam lahko služi: Teorem o obstoju in edinstvenosti: demonstracija, primeri in vaje

(-2x)² + 2 = 0

Rešitev

Enačba je preurejena na naslednji način:

(-2x)² = -2

Nato vzemite kvadratni koren v obeh članih

√ ((-2x)²) = √ (-2)

± (-2x) = √ (-1 x 2) = √ (-1) √ (2) = i √ (2) = √2 i

Potem se končno dobi X:

x = ± √2 / 2 i

To pomeni, da obstajata dve možni rešitvi:

x = (√2 / 2) i

Ali to drugo:

x = - (√2 / 2) i

- Vaja 5

Poiščite vrednost z, ki jo definira::

Z = √ (-9) √ (-4) + 7

Rešitev

Vemo, da je kvadratni koren negativnega resničnega števila namišljeno število, na primer √ (-9) je enak √ (9) x √ (-1) = 3i.

Po drugi strani je √ (-4) enak √ (4) x √ (-1) = 2i.

Tako da lahko prvotno enačbo nadomestimo z:

3i x 2i - 7 = 6 i² - 7 = 6 (-1) -7 = -6 -7 = -13

- Vaja 6

Poiščite vrednost z, ki je posledica naslednje delitve dveh zapletenih števil:

Z = (9 - i²) / (3 + i)

Rešitev

Ekspresijski števec lahko upošteva z naslednjo lastnostjo:

Razlika v kvadratih je produkt vsote glede na razliko binoma, ne da bi dvignili kvadrat.

Tako:

Z = [(3 - i) (3 + i)] / (3 + i)

Nastali izraz se nato poenostavi s preostalo

Z = (3 - i)

Reference

1. Earl, r. Zapletene številke. Okrevano od: matematike.vol.AC.Združeno kraljestvo.
2. Figuera, j. 2000. Matematika 1. Raznovrstno. Co-Bo izdaje.
3. Hoffmann, J. 2005. Izbira vprašanj matematike. Monfort Publications.
4. Jiménez, r. 2008. Algebra. Dvorana Prentice.
5. Wikipedija. Namišljena številka. Pridobljeno iz: v.Wikipedija.org