Komplementarni koti, ki in kako se izračunajo, primeri, vaje

Dva ali več kotov sta komplementarni koti Če vsota njegovih ukrepov ustreza pravemu kotu. Kot je znano, je merilo desnega kota v stopinjah 90 °, v radianih pa π/2.

Na primer, dva kota, ki mejita na hipotenuzo trikotnika pravokotnika, se med seboj dopolnjujeta, saj je vsota njihovih ukrepov 90 °. Naslednja številka je v zvezi s tem zelo ponazoriva:

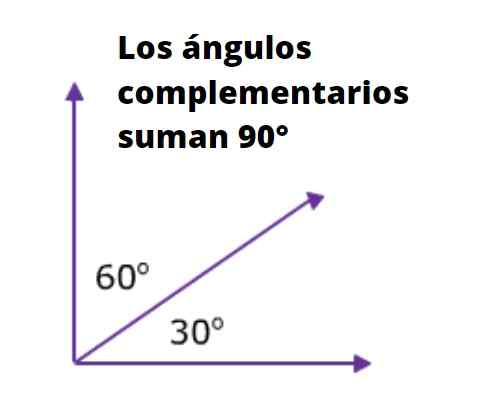
Slika 1. Na levi strani je več kotov s skupno točko. Na desni kot 60 °, ki dopolnjuje kot α (alfa). Vir: f. Zapata.

Slika 1 prikazuje skupno štiri kote. α in β se dopolnjujeta, saj sta v bližini in njen polna vsota pravi kot. Podobno β dopolnjuje γ, kjer sledi, da sta γ in α enaka merila.

Ker je vsota α in δ enaka 90 stopinjah, lahko rečemo, da sta α in δ komplementarna. Poleg tega imata β in Δ enaka dopolnilna α, lahko rečemo, da imata β in Δ enak ukrep.

 [TOC]

Primeri dopolnilnih kotov

V naslednjih primerih je treba najti neznane kote, navedene z zasliševanjem na sliki 2.

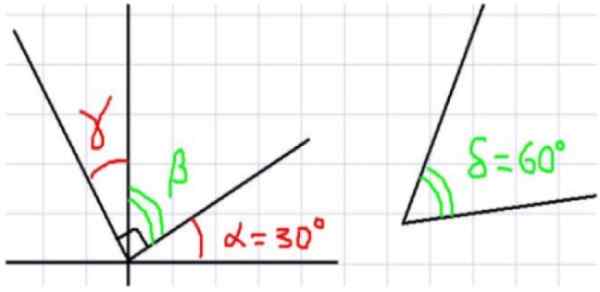
Slika 2. Različni primeri dopolnilnih kotov. Vir: f. Zapata.

- Primeri A, B in C

Naslednji primeri so v vrstnem redu zapletenosti.

Primer a

Na zgornji sliki imamo, da se sosednji koti α in 40 ° seštevata do desnega kota. To je α + 40 ° = 90 °, torej α = 90 °- 40 ° = 50 °.

Primer b

Ker se β dopolnjuje s kotom 35 °, potem β = 90 ° - 35 ° = 55 °.

Vam lahko služi: Orthoedro: formule, območje, prostornina, diagonala, primeri

Primer c

Na sliki 2C vsota γ + 15 ° + 15 ° = 90 °. To pomeni, da γ dopolnjuje kot 30 = 15 ° + 15 °. Tako da:

γ = 90 °- 30 ° = 60 °

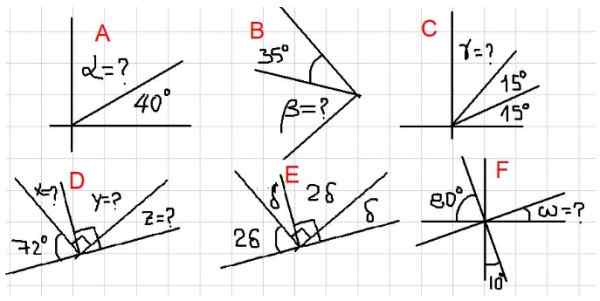
- Primeri D, E in F

V teh primerih je vključenih več kotov. Za iskanje neznank mora bralec uporabiti koncept komplementarnega kota tolikokrat, kolikor je potrebno.

Primer d

Ker je x dopolnjuje s 72 °, sledi, da je x = 90 ° - 72 ° = 18 °. Poleg tega je dopolnjen z x, potem y = 90 ° - 18 ° = 72 °.

Končno se Z dopolnjuje in. Iz vsega zgoraj navedenega izhaja, da:

Z = 90 ° - 72 ° = 18 °

Primer e

Kota δ in 2δ sta torej dopolnjena, torej Δ + 2Δ = 90 °.

To je 3Δ = 90 °, kar pomeni, da je Δ = 90 ° / 3 = 30 °.

Primer f

Če pokličemo kot med ω in 10. Kjer sledi, da u = 80 °. Ker se u dopolnjuje z ω, potem ω = 10 °.

Vaje

Spodaj so predlagane tri vaje. V vseh njih je treba vrednost kotov A in B najti v stopinjah, tako da so razmerja, prikazana na sliki 3, izpolnjena.

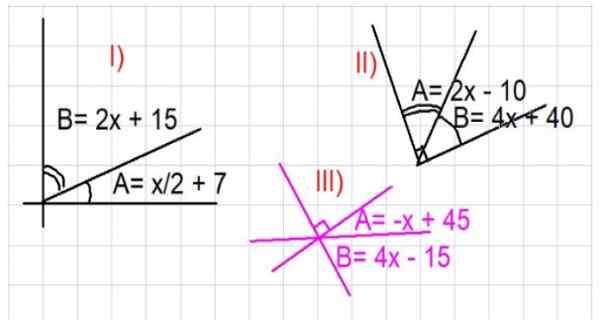Slika 3. Ilustracije za komplementarne kote. Vir: f. Zapata.

- Vaja 1

Določite vrednosti kotov A in B dela I) slike 3.

Rešitev

Iz prikazane slike je razvidno, da sta a in b komplementarna, torej a + b = 90 °. Izraz A in B se nadomesti kot funkcija X, podana v delu I):

Vam lahko služi: konvergenčni radio: definicija, primeri in vaje rešene

(x/2 + 7) + (2x + 15) = 90

Nato so izrazi pravilno razvrščeni in dobimo preprosto linearno enačbo:

(5x/2) + 22 = 90

Odštevanje 22 v obeh članih je:

5x/2 = 90 -22 = 68

In končno je vrednost X očiščena:

x = 2*68/5 = 136/5

Zdaj najdemo kot, ki nadomešča vrednost x:

A = (136/5)/2 +7 = 103/5 = 20,6 °.

Medtem ko je kot B:

B = 2*136/5 + 15 = 347/5º = 69,4 ° .

- Vaja 2

Poiščite vrednosti kotov A in B slike II, slika 3.

Rešitev

Spet kot a in b sta komplementarni koti, morate: a + b = 90 °. Zamenjava izraza A in B kot funkcije X, ki je navedena v delu II) slike 3 je:

(2x - 10) + (4x +40) = 90

Podobni izrazi so združeni za pridobitev enačbe:

6 x + 30 = 90

Dobimo delitev obeh članov med 6:

x + 5 = 15

Kjer sledi, da je x = 10 °.

Zato:

A = 2*10 - 10 = 10 °

B = 4*10 + 40 = 80 °.

- Vaja 3

Določite vrednosti kotov A in B dela III) slike 3.

Rešitev

Slika je skrbno analizirana tako, da išče komplementarne kote. V tem primeru morate + b = 90 stopinj. Nadomeščanje izraza A in B kot funkcije X, ki je podana na sliki, imate:

(-X +45) + (4x -15) = 90

3 x + 30 = 90

Delitev obeh članov za 3 je naslednje:

x + 10 = 30

Kjer sledi, da je x = 20 °.

To pomeni, da je kot A = -20 +45 = 25 °. In v svojem delu: B = 4*20 -15 = 65 °.

Pravokotne strani kotov

Govori se, da sta dva kota pravokotne strani Če ima vsaka stran ustrezno pravokotno v drugi. Naslednja slika pojasnjuje koncept:

Vam lahko služi: sestavljeno nasledstvo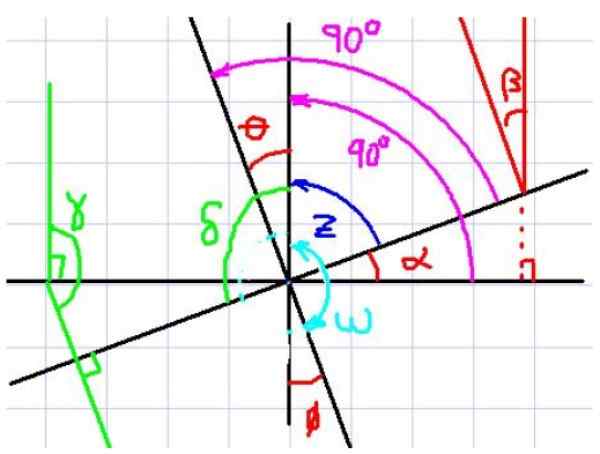Slika 4. Pravokotne strani kotov. Vir: f. Zapata.

Na sliki 4 opazimo kota α in θ, na primer. Zdaj opazite, da ima vsak kot ustrezen pravokotni pod drugim kotom.

Vidimo tudi, da imata α in θ enak komplementarni kot z, Zato opazovalec takoj ugotovi, da imata α in θ enak ukrep. Zdi se, da če imata dva kota pravokotne strani med seboj, sta enaka, a poglejmo drug primer.

Zdaj razmislite o kotih α in ω. Ta dva kota imata tudi ustrezne pravokotne strani, vendar ni mogoče reči, da sta enakovredna, saj je eden akuten, drugi.

Upoštevajte, da je ω + θ = 180 °. Poleg θ = α. Če ta izraz Z zamenjate v prvi enačbi:

Δ + α = 180 °, saj sta Δ in α kota medsebojno pravokotnih strani.

Splošno pravilo za pravokotne strani kotov 

Iz prej omenjenega pravila, ki se vedno izpolnjuje, da imajo koti pravokotne strani lahko vzpostavljene:

Če sta dva kota medsebojno pravokotne strani, potem sta enaka, če sta oba akutna ali oba obljubna. V nasprotnem primeru, če je eden akuten, drugi pa je obljubljen, potem so dodatni, to je, da dodajo 180 °.

Z uporabo tega pravila in glede na kote slike 4 lahko potrdimo naslednje:

α = β = θ = φ

γ = δ

Z ω dodatnim kotom α, β, θ in φ.

Reference

1. Baldor, j. Do. 1973. Ravna in vesoljska geometrija. Srednjeameriška kulturna. 
2. Matematični zakoni in formule. Sistemi za merjenje kotov. Pridobljeno od: Ingemecanica.com.
3. Wentworth, g. Geometrija planeta. Okreval od: Gutenberg.org.
4. Wikipedija. Komplementarni koti. Okrevano od: je.Wikipedija.com
5. Wikipedija. Transporter. Okrevano od: je.Wikipedija.com
6. Zapata f. Goniometer: Zgodovina, deli, delovanje. Pridobljeno iz: Lifer.com