Osrednje simetrične lastnosti, primeri in vaje

Dve točki A in ' Centralna simetrija Glede točke ali ko se segment AA "skozi njega in je tudi sredi točke AA". Do točke ali je poklican Simetrijski center.

Osrednja simetrika ABC trikotnika glede na eno točko ali je še en trikotnik A'B'c ', ki ima naslednje značilnosti:

-Homologni segmenti so enake dolžine 

-Njihovi ustrezni koti imajo enak ukrep.

Slika 1. ABC Triangle in njegov simetrični a'b'c '. Vir: f. Zapata.

Na sliki 1 ABC trikotnik (rdeča) in njegov osrednji simetrični a'b'c '(zelena) glede na središče simetrije ali. 

Na tej isti sliki bi pozorni opazovalec spoznal, da je enak rezultat dosežen z uporabo izvirnega vrtenja trikotnika, dokler je 180 ° in osredotočen na oz.

Zato je osrednja simetrija enakovredna 180 ° zavoju glede na središče simetrije.

[TOC]

Lastnosti osrednje simetrije

Osrednja simetrija ima naslednje lastnosti:

-Simetrijski center je sredi točke segmenta, ki se pridruži točki s svojo simetrično.

-Simetrična točka drugega, ki se nahaja v središču simetrije, sovpada s središčem simetrije.

-Osrednja simetrika trikotnika je skladen trikotnik (enak).

-Slika po osrednji simetriji oboda je še en obod enakega polmera.

-Krog ima osrednjo simetrijo glede na svoj center.

Slika 2. Oblikovanje z osrednjo simetrijo. Vir: Pixabay.

-Elipse ima osrednjo simetrijo glede na njegovo središče.

-Segment ima osrednjo simetrijo glede na svojo sredino.

-Enakostranski trikotnik nima osrednje simetrije glede na svoj center, saj simetrična, čeprav skladna s prvim, daje enakostranični trikotnik.

Lahko vam služi: y = 3sen (4x) funkcijsko obdobje

-Kvadri imajo osrednjo simetrijo glede na njihov center.

-Pentagonu nima osrednje simetrije glede na njegovo središče.

-Redni poligoni imajo osrednjo simetrijo, ko imajo številne strani navora.

Primeri

Merila simetrije imajo veliko aplikacij v znanosti in inženiringu. Osrednja simetrija je prisotna v naravi, na primer ledeni kristali in pajčevine imajo tovrstno simetrijo.

Poleg tega je veliko težav enostavno rešiti, ko se uporablja obstoj centralne simetrije in drugih vrst simetrije. Zato je priročno hitro prepoznati, ko se zgodi.

Slika 3. Ledeni kristali imajo osrednjo simetrijo. Vir: Pixabay.

Primer 1

Glede na točko P koordinat (a, b) morate najti koordinate njegovega simetričnega p 'glede izvora ali koordinat (0, 0).

Prva stvar je, da sestavite P 'P', za katero je narisana črta, ki poteka skozi izvor ali in skozi točko P. Enačba te vrstice je y = (b/a) x.

Zdaj pa pokličimo (a ', b') koordinate simetrične točke p '. Točka str. Poleg tega mora biti razdalja OP enaka OP ', ki analitično piše tako:

√ (a² + b²) = √ (a '² + B '² )

Sledi zamenjava b '= [(b/a).A '] v prejšnjem izrazu in kvadrat na obeh straneh enakosti, da odpravite kvadratni koren: (a² + b²) = [a '² + (b²/do²).do '²]

Z pridobivanjem skupnega faktorja in poenostavitve je dosežen '² = a². Ta enačba ima dve resnični rešitvi: a '= +a ali a' = -a. 

Za pridobitev b 'ponovno uporabimo b' = (b/a) a '. Če je pozitivna raztopina A zamenjana, je doseženo, da je B '= B. In ko se negativna rešitev zamenja, potem b '= -b. 

Vam lahko služi: kakšnih je 7 elementov oboda?

Pozitivna rešitev daje za p 'isto točko P, zato je izključena. Negativna rešitev zagotovo ponuja koordinate simetrične točke:

P ': (-a, -b)

Primer 2

Potrebno je dokazati, da imata AB segment in njegov simetrični osrednji A'b 'enako dolžino.

Začenši s koordinatami točke A, ki so (sekira, ay) in tistim iz točke B: (bx, by), dolžina AB je podana z:

D (AB) = √ ((BX - AX)² + (Avtor - ay)² )

Po analogiji bo imel simetrični segment A'B 'dolžino, ki jo daje:

D (A'B ') = √ ((BX' - AX ')² + (Z ' - ay')² )

Koordinate simetrične točke A 'AX' = -ax in ay '= -ay. Podobno so tisti, ki so B 'BX' = -BX in z '= -By. Če se te koordinate zamenjajo v enačbi razdalje D (a'b '), imate:

D (a'b ') = √ ((-bx + sekira)² + (-By + Ay)²) To je enakovredno:

 √ ((bx - sekira)² + (Avtor - ay)²) = D (ab)

Dokazano, da imata oba segmenta enako dolžino.

Rešene vaje

- Vaja 1

Na analitični način dokazujte, da je centralni simetrični ali krog polmera r in središča ALI, enak izvirni obod.

Rešitev

Enačba polmera R in sredinskega kroga (0,0) je:

x² + in² = R² (Enačba oboda c)

Če v vsaki točki P oboda in koordinat (x, y) najdemo njegovo simetrično koordinato p '), je enačba simetričnega oboda:

x '² + in² = R² (Simetrična enačba oboda c ')

Zdaj se sklicujemo na rezultat 1, ki sklepa, da so koordinate točke P ', simetrične na P in koordinate (a, b), (-a, -b). 

Toda v tej vaji ima točka P koordinate (x, y), tako da bo njegov simetrični p 'koordinate x' = -x e y '= -y. Nadomeščanje tega v simetrični enačbi oboda je:

Vam lahko služi: Rhomboid: značilnosti, kako odnesti obod in območje

(-X)² + (in)² = R²

Kar je enakovredno: x²+ in² = R², sklepa, da je osrednja simetrika kroga glede na njegovo središče sam obod.

- Vaja 2

Na geometrijski način dokazujte, da centralna simetrija ohranja kote.

Rešitev

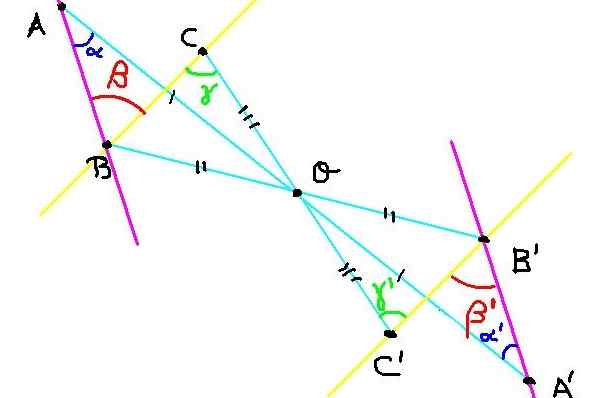Slika 4. Konstrukcija simetričnih točk za vajo 2. Vir: f. Zapata.

Na ravnini so tri točke A, B in C. Njegovi simetrični a ', b' in c 'so zgrajeni glede na središče simetrije ali, kot je prikazano na sliki 4. 

Zdaj moramo dokazati, da ima kot ∡abc = β enak ukrep kot kot ∡a'b'c '= β' '.

Ker sta C in C 'simetrična, potem oc = oc'. Podobno ob = ob 'y oa = oa'. Po drugi strani pa kot ∡boc = ∡b'oc ', ker je nasprotoval vrhovi.

Potem sta trikotnika boc in b'oc 'skladna, ker imata enak kot med dvema stranicama.

Ker je BOC skladen z b'oc ', potem koti  γ in γ ' So enaki. Toda ti koti poleg izpolnjevanja γ = γ ' So notranji nadomestni med črtami BC in B'C, kar pomeni, da je linija BC vzporedna z B'C '.

Podobno je BAA skladen z b'oa 'tistega, kar sledi α = α ' . Ampak  α in α ' So notranji nadomestni koti med črtami BA in B'a, od katerih je sklenjeno, da je črta BA vzporedna z B'a '.

Ker ima kot ∡abc = β svoje vzporedne strani s kotom ∡a'b'c '= β' in sta tudi oba akutna, je sklenjeno, da:

∡abc = ∡a'b'c '= β = β' '

Na ta način dokazuje, da centralna simetrija ohranja mero kotov.

Reference

1. Baldor, j. Do. 1973.Ravna in vesoljska geometrija. Srednjeameriška kulturna. 
2. Matematični zakoni in formule. Sistemi za merjenje kotov. Pridobljeno od: Ingemecanica.com.
3. Wentworth, g. Geometrija planeta. Okreval od: Gutenberg.org.
4. Wikipedija. Centralna simetrija. Okrevano od: je.Wikipedija.com
5. Wikipedija. Transporter. Okrevano od: je.Wikipedija.com
6. Zapata f. Notranji in zunanji konjugatni koti. Pridobljeno iz: Lifer.com