GAUSS-SEIDER METOM Pojasnilo, aplikacije, primeri

On Metoda Gauss-Seidel Iterativni postopek je najti približne rešitve sistema linearnih algebrskih enačb z poljubno izbrano natančnostjo. Metoda velja za kvadratne matrike z ne -nulskimi elementi v njegovih diagonalih in konvergenca je zagotovljena, če je matrica diagonalno prevladujoča.

Ustvaril ga je Carl Friedrich Gauss (1777-1855), ki je leta 1823 zasebno predstavil enemu od njegovih študentov. Nato ga je uradno objavil Philipp Ludwig von Seidel (1821-1896) leta 1874, od tod tudi ime obeh matematikov.

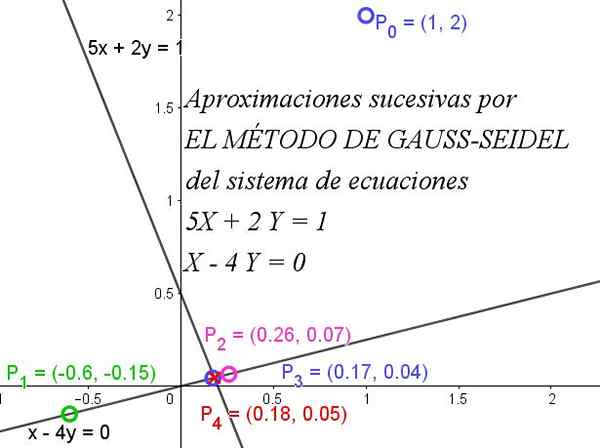
Slika 1. Metoda Gauss-Seidel se hitro zbliža, da pridobi sistem enačb. Vir: f. Zapata.

Za popolno razumevanje metode je treba vedeti, da je matrica diagonalno prevladujoča, kadar je absolutna vrednost diagonalnega elementa vsake vrstice večja ali enaka vsoti absolutnih vrednosti drugih elementov iste vrstice.

Matematično je izraženo na naslednji način:

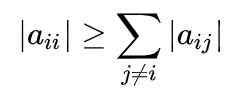
[TOC]

Pojasnilo skozi preprost primer

Za ponazoritev, kaj bo metoda Gauss-Seidel opravila preprost primer, v katerem lahko v spodnjem sistemu linearnih enačb 2 × 2 najdete vrednosti X in Y:

5x + 2y = 1

X - 4y = 0

Korake za sledenje

1- Najprej morate ugotoviti, ali je konvergenca varna. Takoj opazimo, da je dejansko diagonalno prevladujoč sistem, saj ima v prvi vrstici prvi koeficient večjo absolutno vrednost kot drugi v prvi vrsti:

| 5 |> | 2 |

Prav tako je tudi drugi koeficient druge vrste diagonalno prevladujoč:

| -4 |> | 1 |

2- Spremenljivke x in y sta jasni: 

X = (1 - 2y)/5

Y = x/4

3- Postavljena je začetna poljubna vrednost, imenovana "seme": xo = 1, me = 2.

4

Lahko vam služi: ocena po presledkih

X1 = (1 - 2 me)/5 = (1 - 2 × 2)/5 = -3/5 

Y1 = x1 / 4 = (-3/5) / 4 = -3/20 

5- nadaljujte na podoben način, da dosežete drugi približek raztopine sistema enačb:

X2 = (1 - 2 y1)/5 = (1 - 2x (-3/20))/5 = 13/50 

Y2 = x2/4 = (13/50)/4 = 13/200

6- tretjina iteracija:

X3 = (1 - 2 y2)/5 = (1 - 2 (13/200))/5 = 87/500

Y3 = x3/4 = (87/500)/4 = 87/2000

7- Četrta iteracija, kot končna iteracija tega ilustrativnega primera:

X4 = (1 - 2 y3)/5 = (1 - 2 (87/2000))/5 = 913/5000

Y4 = x4/4 = (913/5000)/4 = 913/20000

Te vrednosti precej dobro sovpadajo z rešitvijo, ki jo najdemo z drugimi metodami ločljivosti. Bralec ga lahko hitro preveri s pomočjo spletnega matematičnega programa.

Analiza metode

Kot je razvidno, je treba pri metodi Gauss-Seidel v naslednji spremenljivki zamenjati približne vrednosti, pridobljene za prejšnjo spremenljivko v istem koraku. To ga razlikuje od drugih iterativnih metod, kot je Jacobi, v katerih vsak korak zahteva pristope do prejšnje faze. 

Metoda Gauss-Seidel ni vzporedna postopek, medtem ko je Gauss-Jordan. To je tudi razlog, da ima Gauss-Seidel metoda hitrejše konvergenčne korake-metoda Jordanije.

Kar zadeva diagonalno prevladujoče matrično stanje, to ni vedno zadovoljno. Vendar je v večini primerov dovolj, da si izmenjate vrste originalnega sistema, da izpolnite pogoj. Poleg tega se metoda skoraj vedno zbliža, tudi če stanje diagonalne prevlade ni izpolnjeno.

Prejšnji rezultat, pridobljen s štirimi ponovitvami metode Gauss-Seidel, je mogoče zapisati na decimalen način:

Vam lahko služi: koliko osi simetrije ima krog?

X4 = 0,1826

Y4 = 0,04565

Natančna rešitev dvignjenega sistema enačb je:

X = 2/11 = 0,1818

Y = 1/22 = 0,04545.

Torej samo s 4 ponovitvami dosežemo rezultat s tisočjo natančnosti (0,001).

Slika 1 prikazuje, kako se zaporedne iteracije hitro zbližajo do natančne rešitve.

Prijave

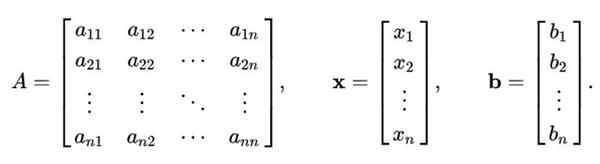
Metoda Gauss-Seidel ni omejena le na sistem linearnih enačb 2 × 2. Zgornji postopek je mogoče posplošiti za reševanje linearnega sistema n enačbe s n Neznanke, ki so predstavljene matrične, kot je ta:

Do X = b

Kje Do To je matrica n x n, medtem X To je vektorska n komponente spremenljivk, ki jih je treba izračunati; in b Je vektor, ki vsebuje vrednosti neodvisnih izrazov.

Če želite posplošiti zaporedje iteracij, uporabljenih v ilustrativnem primeru, v sistemu n x n, ki želi izračunati spremenljivko Xi, Uporablja se naslednja formula:

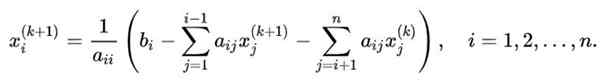
V tej enačbi:

- k Je indeks za vrednost, pridobljeno v iteraciji k.

-K+1 Označuje novo vrednost v naslednjem.

Končno število iteracij se določi, kadar je vrednost, dobljena v iteraciji K+1 se razlikuje od pridobljenega takoj prej, v znesku ε, ki je natančno želena natančnost.

Primeri metode Gauss-Seidel

- Primer 1

Napišite splošni algoritem, ki vam omogoča izračun približnega vektorja rešitve X linearnega sistema NXN enačb, glede na matriko koeficienta Do, Vektor neodvisnih izrazov b, Število ponovitev (iter) in začetno ali "seme" vektorja X.

Rešitev

Algoritem je sestavljen iz dveh "za" cikle, enega za število iteracij, drugi pa za število spremenljivk. Bilo bi naslednje:

Za k ∊ [1 ... iter]

Za i ∊ [1… n]

X [i]: = (1/a [i, i])*(b [i] - ∑_{J = 1}ⁿ(A [i, j]*x [j]) + a [i, i]*x [i])

Vam lahko služi: decimalni zapis

- Primer 2

Preverite delovanje prejšnjega algoritma s prijavo na matematično programsko opremo STATH STUDIO brezplačno in brezplačno, na voljo za Windows in Android. Kot primer vzemite primer matrice 2 × 2, ki nam je služila za ponazoritev metode Gauss-Seidel.

Rešitev

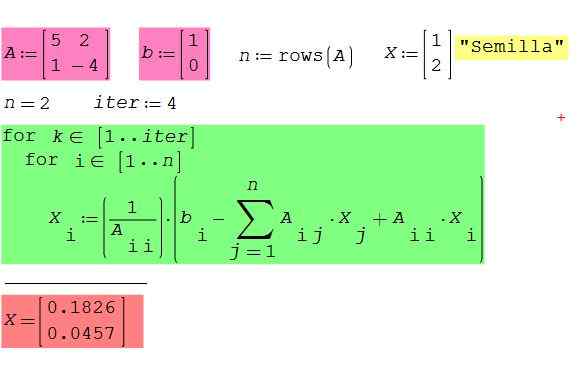Slika 2. Sistem enačb primera 2 x 2 z uporabo programske opreme STATH STUDIO. Vir: f. Zapata.

- Primer 3

Uporabite algoritem Gauss-Seidel za naslednji sistem 3 × 3 enačbe, ki je bil že predhodno naročen tako, da prevladujejo diagonalni koeficienti (torej večje absolutne vrednosti kot absolutne vrednosti koeficientov koeficientov iste vrstice):

9 x1 + 2 x2 - x3 = -2

7 x1 + 8 x2 + 5 x3 = 3

3 x1 + 4 x2 - 10 x3 = 6

Uporabite ničelni vektor kot seme in upoštevajte pet ponovitev. Komentar o rezultatu.

Rešitev

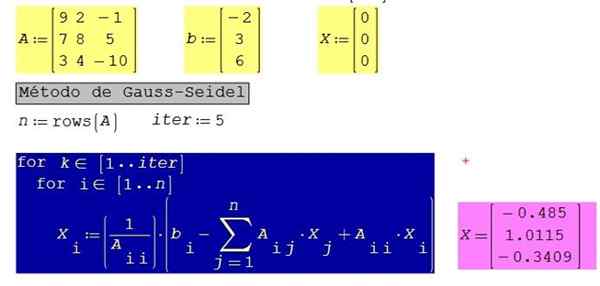Slika 3. Rešitev sistema enačb razrešenega primera 3 z uporabo Smath Studio. Vir: f. Zapata.

Za isti sistem z 10 iteracijami namesto 5 dobimo naslednji rezultati: x1 = -0.485; X2 = 1.0123; X3 = -0.3406

To kaže, da je dovolj s petimi ponovitvami, da dobimo tri natančne decimale in da metoda hitro prenaša rešitev.

- Primer 4

S pomočjo daje algoritma Gauss-Seidel poiščite rešitev sistema 4 × 4 enačbe, ki se pojavi spodaj:

10 x1 - x2 + 2 x3 + 0 x4 = 6

-1 x1 + 11 x2 - 1 x3 + 3 x4 = 25

2 x1 - 1 x2 + 10 x3 - 1 x4 = -11

0 x1 + 3 x2 - 1 x3 + 8 x4 = 15

Za začetek metode uporabite to seme:

x1 = 0, x2 = 0, x3 = 0 in x4 = 0

Razmislite o 10 iteracijah in ocenite napako rezultata, v primerjavi s številko iteracije 11.

Rešitev

Slika 4. Rešitev sistema enačb razrešenega primera 4 z uporabo Smath Studio. Vir: f. Zapata.

V primerjavi z naslednjo iteracijo (številka 11) je rezultat enak. Največje razlike med obema iteracijama so vrstnega reda 2 × 10^-8, Kar pomeni, da ima prikazana rešitev natančnost vsaj sedem decimalk.

Reference

1. Iterativne metode rešitve. Gauss-Seidel. Okreval od: cimat.mx
2. Numerične metode. Gauss-Seidel. Obnovi se od: test.Cua.UAM.mx
3. Številčna: metoda Gauss-Seidel. Okrevano od: učite se v lineji.ti.Edu.co
4. Wikipedija. Metoda Gauss-Seidel. Pridobljeno iz: v. Wikipedija.com
5. Wikipedija. Metoda Gauss-Seidel. Okrevano od: je.Wikipedija.com