Ukrepi spremenljivosti

Slika 1.- Najbolj znani ukrepi spremenljivosti. Vir: f. Zapata.

Kaj so ukrepi spremenljivosti?

The Ukrepi spremenljivosti, Imenujejo se tudi disperzijski ukrepi, to so statistični kazalniki, ki kažejo, kako tesni ali oddaljeni so podatki njihove aritmetične srednje vrednosti. Če so podatki blizu povprečju, je porazdelitev koncentrirana in če so daleč, je potem razpršena porazdelitev.

Obstaja veliko ukrepov za spremenljivost, med najbolj znanimi je:

• Domet
• Povprečno odstopanje
• Odstopanje
• Standardni odklon

Ti ukrepi dopolnjujejo osrednje tendenčne ukrepe in so potrebni za razumevanje porazdelitve pridobljenih podatkov in izvleči čim več informacij.

Domet

Območje ali pot meri amplitudo nabora podatkov. Za določitev njegove vrednosti najdemo razliko med najvišjo vrednostjo x_Max in najmanj x vrednost_min:

R = x_Max - x_min

Če podatki niso ohlapni, vendar jih razvrstijo po intervalu, se obseg izračuna z razliko med zgornjo mejo zadnjega intervala in spodnjo mejo prvega intervala.

Kadar je obseg majhna vrednost, to pomeni, da so vsi podatki precej blizu drug drugemu, vendar velik razpon kaže, da je veliko spremenljivosti. Očitno je, da poleg zgornje meje in spodnje meje podatkov obseg ne upošteva vrednosti med njimi, zato ga ni priporočljivo uporabiti, kadar je številka podatkov velika.

Vendar je takojšen ukrep za izračun in ima enake podatkovne enote, zato ga je enostavno razlagati.

Primer ranga

Nato je seznam na voljo s številom ciljev, označenih med vikendom, v nogometnih ligah iz devetih držav:

Vam lahko služi: kakšni so delitve 30? (Pojasnilo)

40, 32, 35, 36, 37, 31, 37, 29, 39

To je nabor podatkov brez razvrščanja. Da bi našli domet, jih naročijo, da jih naročijo od najmanj do največjega:

29, 31, 32, 35, 36, 37, 37, 39, 40

Podatki z najvišjo vrednostjo so 40 ciljev, tisti z najnižjo vrednostjo pa 29 ciljev, zato je razpon:

R = 40–29 = 11 ciljev.

Lahko se šteje, da je obseg majhen v primerjavi z podatki o minimalni vrednosti, kar je 29 ciljev, zato je mogoče domnevati, da podatki nimajo velike variabilnosti.

Povprečno odstopanje

Ta ukrep spremenljivosti se izračuna s povprečjem absolutnih vrednosti odstopanj glede na povprečje. Označevanje povprečnega odstopanja kot d_M, Za podatke, ki niso združeni, se povprečno odstopanje izračuna z naslednjo formulo:

Kjer je n število razpoložljivih podatkov, x_Yo Predstavlja vsak podatki in X̄ je povprečje, ki se določi z dodajanjem vseh podatkov in delitvijo med n:

Povprečna odstopanje omogoča, da v povprečju vemo, koliko enot podatkov odstopa od aritmetične srednje vrednosti in ima prednost, da ima enake enote kot podatki, s katerimi deluje.

Primer srednjega odstopanja

Po podatkih območja je število označenih ciljev:

40, 32, 35, 36, 37, 31, 37, 29, 39

Če želite najti srednje D odstopanje_M Od teh podatkov je treba najprej izračunati aritmetično srednjo vrednost:

In zdaj, ko je znana vrednost X̄, nadaljujemo z iskanjem povprečnega odstopanja_M:

= 2.99 ≈ 3 cilji

Zato lahko rečemo, da se v povprečju podatki oddaljijo približno v 3 povprečnih ciljih, ki so 35 ciljev, in kot je navedeno.

Vam lahko služi: hiperbola

Odstopanje

Povprečno odstopanje je veliko tanjši ukrep spremenljivosti kot območje, vendar kot izračunamo z absolutno vrednostjo razlik med vsakim podatkom in povprečjem, ne ponuja večje vsestranskosti z algebrskega vidika.

Zato je varianta prednostna, kar ustreza povprečju kvadratne razlike vsakih podatkov s srednjo vrednostjo in se izračuna po formuli:

V tem izrazu² označuje varianco in kot vedno x_Yo predstavlja vsak od podatkov, x̄ je povprečje in n skupni podatki.

Pri delu z vzorcem namesto populacije je raje izračunati varianco, kot je ta:

Razlika s prejšnjo formulo je v tem, da je v imenovalcu n - 1 namesto n. Zgodi se, da odstopanje vzorca podcenjuje varianco populacije, iz katere je bila ekstrahirana, vendar ne, kadar je razdeljen na n - 1. V nekaterih besedilih se prikaže izraz z imenom kvazi-variza.

V vsakem primeru je značilno, da je odstopanje vedno pozitiven znesek, vendar je povprečje kvadratnih razlik, pomembno je upoštevati, da nima enakih enot kot tistih podatkov.

Primer variance

Za izračun variance podatkov primerov območja in povprečnega odstopanja se ustrezne vrednosti zamenjajo in navedena vsota. V tem primeru je izbran za delitev med N-1:

= 13.86

Standardni odklon

Varianca nima enake enote kot v študiji spremenljivke, na primer, če podatki prihajajo v metrih, varianca povzroči kvadratne metre. Ali v primeru ciljev, ki bi jih bilo v ciljih, kar nima smisla.

Vam lahko služi: kakšni so elementi prispodobe? (Deli)

Zato je določen standardni odklon, imenovan tudi Tipično odstopanje, Kot kvadratni koren variance:

S = √s²

Na ta način je merilo spremenljivosti podatkov v istih enotah kot te in nižja je vrednost S, bolj so razvrščeni podatki okoli povprečja.

Varianta in standardni odklon sta ukrepi spremenljivosti, ki jih je treba izbrati, kadar je aritmetična srednja vrednost osrednje težnje, ki najbolje opisuje vedenje podatkov.

In to je, da ima standardni odklon pomembno lastnost, znano kot Chebyshevovo izrek: vsaj 75% opazovanj je v intervalu, ki ga določa x̄ ± 2s. Z drugimi besedami, 75% podatkov je kvečjemu na razdalji, ki je enaka 2S v povprečju.

Prav tako je vsaj 89% vrednosti na razdalji 3s od povprečja, kar je mogoče razširiti, pod pogojem, da je na voljo veliko podatkov in sledijo običajni porazdelitvi.

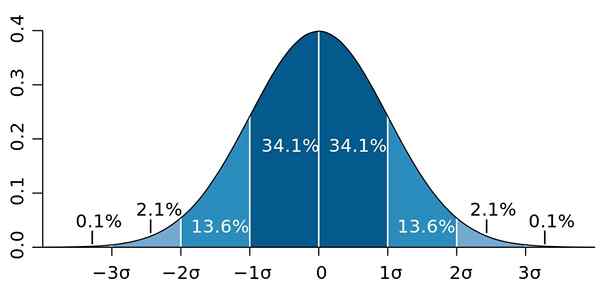
Slika 2.- Če podatki sledijo običajni porazdelitvi, 95.4 sta dva standardna odstopanja na obeh straneh povprečnega. Vir: Wikimedia Commons.

Primer standardnega odklona

Standardni odklon podatkov, predstavljenih v prejšnjih primerih, je:

S = √s² = √13.86 = 3.7 ≈ 4 cilji