Porazdeli f značilnosti in vaje rešene

The porazdelitev f o Fisher-Snedecor Distribucija je tisto, kar se uporablja za primerjavo odstopanj dveh različnih ali neodvisnih populacij, od katerih vsaka sledi normalni porazdelitvi.

Porazdelitev, ki sledi različici nabora vzorcev ene same običajne populacije, je porazdelitev JI-kvadrata (Χ²) stopnje N-1, če ima vsak od vzorcev niza N elemente.

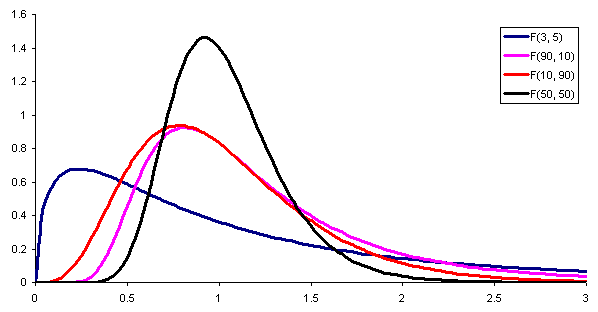
Slika 1. Tu je gostota verjetnosti porazdelitve F z različnimi kombinacijami parametrov (ali stopenj svobode) števca oziroma imenovala. Vir: Wikimedia Commons.

Za primerjavo odstopanj dveh različnih populacij je treba določiti a statistično, to pomeni pomožna naključna spremenljivka, ki omogoča razkritje, ali imata obe populaciji ali ne iste razlike.

Ta pomožna spremenljivka je lahko neposredno količina vzorčnih odstopanj vsake populacije, v tem primeru, če je omenjeni količnik blizu enoti, je dokazano, da imata obe populaciji podobne odstopanja.

[TOC]

Statistika F in njena teoretična porazdelitev

Naključna spremenljivka F ali statistična f, ki jo je predlagal Ronald Fisher (1890 - 1962), je tista, ki se pogosteje uporablja za primerjavo odstopanj dveh populacij in je opredeljena na naslednji način:

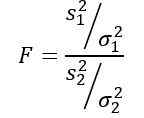
Biti s² Varianta vzorca in σ² Odstopanje prebivalstva. Za razlikovanje vsake od obeh skupin prebivalstva se uporabljata naročnina 1 oziroma 2.

Znano je, da je porazdelitev JI-kvadrata z (N-1) stopnjami svobode tista, ki sledi pomožni (ali statistični) spremenljivki, ki je opredeljena spodaj:

X² = (N-1) s² / σ².

Zato statistika F sledi teoretični porazdelitvi, ki jo daje naslednja formula:

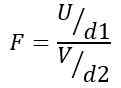
Biti Ali Porazdelitev JI-Square z D1 = n1 - 1 stopnje svobode za prebivalstvo 1 in V Porazdelitev JI-Square z D2 = n2 - 1 Stopnje svobode za prebivalstvo 2.

Vam lahko služi: vektorska algebra

Razmerje, opredeljeno na ta način, je nova porazdelitev verjetnosti, znana kot porazdelitev f z D1 stopnje svobode v števcu in D2 Stopnje svobode v imenovalcu.

Povprečna, moda in odstopanje distribucije f

Polovica

Povprečna porazdelitev F se izračuna na naslednji način:

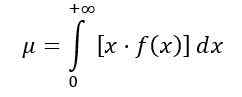
Ker je F (x) gostota verjetnosti porazdelitve F, ki je prikazana na sliki 1 za več kombinacij parametrov ali stopenj svobode.

Lahko napišete gostoto verjetnosti f (x), odvisno od γ funkcije (gama funkcija):

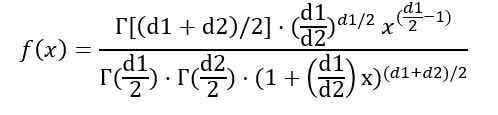
Ko je integral že naveden, je ugotovljeno, da je povprečje porazdelitve F s stopnjami svobode (D1, D2): IS: IS: IS:

μ = d2 / (d2 - 2) z d2> 2

Kjer je razvidno, da je zanimivo povprečje, ni odvisno od stopnje svobode D1 števca.

Moda

Po drugi strani pa je moda odvisna od D1 in D2 in jo daje:

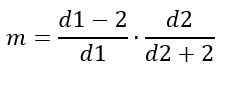
Za d1> 2.

Odstopanje distribucije f

Varianta σ² porazdelitve f se izračuna iz integrala:

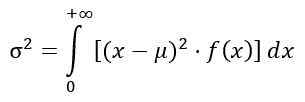
Pridobivanje:

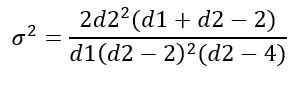
Upravljanje distribucije f

Tako kot druge nenehne porazdelitve verjetnosti, ki vključujejo zapletene funkcije, tudi upravljanje distribucije F izvaja tabele ali programska oprema.

Tabele za distribucijo f

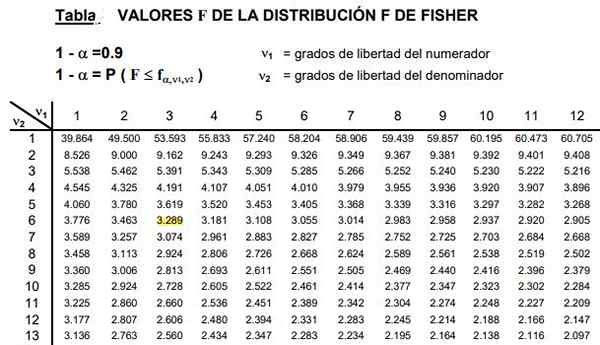Slika 2. Prikazan je del distribucijske tabele F, ki je običajno zelo obsežen, ker obstaja široka kombinacija možnih stopenj svobode D1 in D2.

Tabele vključujejo dva parametra ali stopnje svobode porazdelitve F, stolpec kaže na stopnjo svobode števca in vrstico stopnjo svobode imenovalca.

Vam lahko služi: neenakost trikotnika: demonstracija, primeri, rešene vaje

Slika 2 prikazuje del tabele distribucije F za primer a raven pomembnosti 10%, to je α = 0,1. Vrednost F je poudarjena, ko je d1 = 3 in d2 = 6 z stopnja zaupanja 1- α = 0,9, kar je 90%.

Programska oprema za distribucijo f

Kar zadeva programsko opremo, ki upravlja distribucijo f, je velika raznolikost, od preglednic kot Excel celo specializirani paketi, kot so Minitab, SPSS in R Če naštejem nekaj najbolj znanih.

Treba je opozoriti, da je programska oprema za geometrijo in matematiko Geogebra Ima statistično orodje, ki vključuje glavne distribucije, vključno z distribucijo F. Slika 3 prikazuje porazdelitev F za primer D1 = 3 in D2 = 6 stopnja zaupanja 90%.

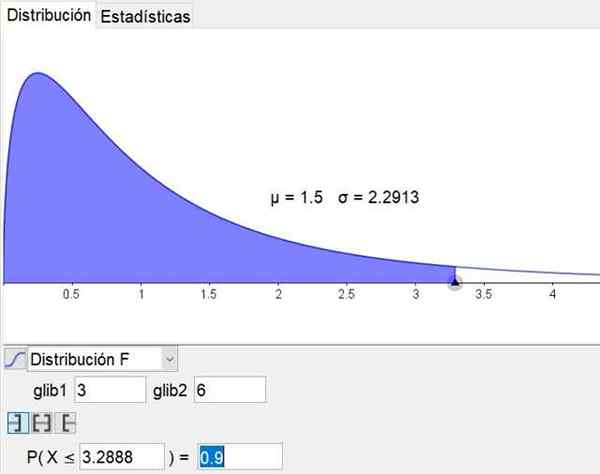Slika 3. Porazdelitev F je prikazana za primer D1 = 3 in D2 = 6 z 90 -odstotno stopnjo zaupanja, pridobljena s statističnim orodjem Geogebra. Vir: Geogebra.org

Rešene vaje

Vaja 1

Razmislite o dveh vzorcih populacije, ki imata enako populacijsko varianco. Če je vzorec 1 velikost N1 = 5 in vzorec 2 je velikost N2 = 10, določite teoretično verjetnost, da je razmerje med ustreznimi odstopanji manjše ali enako 2.

Rešitev

Ne pozabite, da je statistika F opredeljena kot:

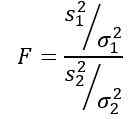
Vendar so nam povedali, da so razlike populacije enake, zato za to vajo velja:

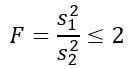
Ker želite vedeti teoretično verjetnost, da je to razmerje med vzorčnimi odstopanji manjše ali enako 2, moramo poznati območje pod porazdelitvijo F med 0 in 2, ki jo lahko dobimo s tabelami ali programsko opremo. Za to je treba upoštevati, da ima zahtevana porazdelitev f d1 = n1 - 1 = 5 - 1 = 4 in d2 = n2 - 1 = 10 - 1 = 9, torej porazdelitev f s stopnjami svobode (4, 9).

Lahko vam služi: niz moči: primeri in vaje

Z uporabo statističnega orodja Geogebra Ugotovljeno je bilo, da je to območje 0.82, zato je sklenjeno, da je verjetnost, da je razmerje med vzorčnimi odstopanji manjše ali enako 2, 82%.

Vaja 2

Obstajata dva procesa izdelave tankih listov. Spremenljivost debeline mora biti čim večja. Odvzetih je 21 vzorcev vsakega postopka. Vzorec procesa ima standardni odklon 1,96 mikronov, medtem ko ima postopek B standardni odklon 2,13 mikronov. Kateri od procesov ima nižjo spremenljivost? Uporabite 5 -odstotno stopnjo zavrnitve.

Rešitev

Podatki so naslednji: SB = 2,13 z NB = 21; SA = 1,96 z Na = 21. To pomeni, da morate sodelovati z porazdelitvijo F (20, 20) stopinj svobode.

Nična hipoteza pomeni, da je varianta populacije obeh procesov enaka, torej σa^2 / σB^2 = 1. Alternativna hipoteza bi pomenila različne odstopanja populacije.

Nato je pod predpostavko enakih odstopanj populacije statistika, izračunana kot: fc = (sb/sa)^2.

Ker je bila stopnja zavrnitve vzeta kot α = 0,05, potem α/2 = 0,025

Porazdelitev F (0.025; 20,20) = 0,406, medtem ko F (0.975; 20,20) = 2,46.

Zato bo ničelna hipoteza resnična, če bo izračunano F skladno: 0,406≤fc≤2,46. Sicer je ničelna hipoteza zavrnjena.

Kot fc = (2,13/1,96)^2 = 1,18 je sklenjeno, da je statistika FC v sprejemanju ničelne hipoteze z gotovostjo 95%. Z drugimi besedami z gotovostjo 95% oba proizvodna procesa imata enako varianco populacije.

Reference

1. F test za neodvisnost. Okreval od: saylordotorg.GitHub.Io.
2. Med val. Statistični podatki, ki se uporabljajo za zdravstvene vede: test F. Okreval od: Medwave.Cl.
3. Verjetnosti in statistike. Porazdelitev f. Pridobljeno iz: Verjetnosti Andestics.com.
4. Triola, m. 2012. Osnovna statistika. 11. Izdaja. Addison Wesley.
5. Ne. Porazdelitev f. Okrevano od: svetovalnega.Cuautitlan2.Ne.mx.
6. Wikipedija. Porazdelitev f. Okrevano od: je.Wikipedija.com