Tehtano povprečje, kako se izračuna, primeri in vaje

The Povprečna teža ali tehtana aritmetična srednja vrednost je osrednji ukrep tendenc, v katerem, na vsako vrednost x_Yo ki lahko vzame spremenljivko x, dodeljen je peso p_Yo. Kot rezultat, z oznako tehtanega povprečja s x_str, Imaš:

S povzetkom vsote je formula za tehtano povprečje:

Kjer n predstavlja količino vrednosti, izbranih iz spremenljivke x.

P_Yo, ki se imenuje tudi Faktor tehtanja, To je merilo pomembnosti, ki ga raziskovalec dodeli vsaki vrednosti. Ta dejavnik je samovoljni in vedno pozitiven.

Pri tem se tehtano povprečje razlikuje od preproste aritmetične srednje vrednosti, ker v tem vsaka od vrednosti x_n Ima enak pomen. Vendar v številnih aplikacijah raziskovalec morda meni, da so nekatere vrednosti pomembnejše od drugih in bodo dodelile težo v skladu z njihovimi merili.

Tu je najbolj znan primer: Recimo, da študent predstavi N Ocene v eni temi in vsi imajo enako težo v končni opombi. V tem primeru bo za izračun končne opombe dovolj, da naredimo preprosto povprečje, torej dodati vse kvalifikacije in rezultat razdelite z n.

Če pa ima vsaka dejavnost drugačno težo, ker nekatere ocenijo pomembnejšo ali bolj zapleteno vsebino, bo treba vsako oceno pomnožiti s svojo težo in nato dodati rezultate, da dobimo končno oceno. Videli bomo, kako izvesti ta postopek v razdelku Rešene vaje.

[TOC]

Primeri

Slika 1. Uteženo povprečje se uporablja pri izračunu indeksa cen potrošnikov, indikator inflacije. Vir: pxhere.

Primer zgoraj opisanih kvalifikacij je eden najbolj značilnih v smislu uporabe tehtanega povprečja. Druga zelo pomembna aplikacija v ekonomiji je Indeks cen potrošnikov tudi Indeks cen potrošnikov IPC, imenovan tudi družinska košara in to služi kot ocenjevalec inflacije v gospodarstvu.

Vam lahko služi: koti in trikotniki

V svoji izdelavi se upošteva vrsta predmetov, kot so hrana in brezalkoholne pijače, oblačila in obutev, zdravila, prevoz, komunikacija, izobraževanje, prosti čas in drugo blago in storitve.

Strokovnjaki vsakemu področju dodelijo uteži, glede na njihov pomen v življenju ljudi. Cene se zbirajo za uveljavljeno obdobje in z vsemi informacijami se izračuna IPC omenjenega obdobja, ki je lahko mesečno, dvomesečno, polletno ali letno, na primer.

Masno središče sistema delcev

V fiziki ima tehtano povprečje pomembno uporabo, ki je izračunati Masovni center sistema delcev. Ta koncept je zelo koristen pri delu z razširjenim telesom, v katerem je treba upoštevati njegovo geometrijo.

Masni center je opredeljen kot točka, na kateri je koncentrirana celotna masa podaljšanega predmeta. Na tej točki lahko sile na primer uporabimo kot težo in tako razložijo njihove premike prevajanja in vrtenja, z istimi tehnikami, s katerimi so delali, ko naj bi bili vsi predmeti delci.

Po preprostosti začne predpostavljati, da je razširjeno telo sestavljeno iz zneska N delcev, vsak od njih z maso m in svojo lokacijo v vesolju: koordinatna točka (x_Yo, in_Yo, z_Yo).

Biti x_Cm Koordinata x Iz centra CM, potem pa:

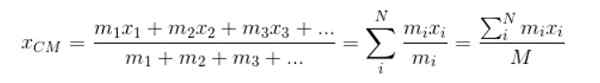
M predstavlja skupno maso sistema. Nadaljuje na enak način za iskanje koordinat in_Cm in z_Cm:

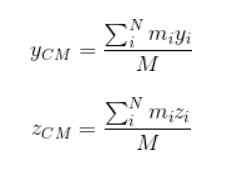
Faktor tehtanja v tem primeru je masa vsakega od delcev, ki predstavljajo razširjeni predmet.

Vam lahko služi: transcendentne funkcije: vrste, definicija, lastnosti, primeri

Pomembne značilnosti množičnega centra

Ko je število delcev zelo veliko, je neprekinjen predmet. V tem primeru je n → ∞ in vsoto nadomeščena z definiranim integralom, katerega omejitve je podana z velikostjo predmeta.

Pomembno je poudariti dejstvo, da na lokaciji množičnega centra ni nujno mase. Na primer v krofnem krofu središče mase bolj ali manj sovpada z geometrijskim središčem Rosquilla.

Slika 2. Masovno središče krofa, dokaj simetričen predmet, je v luknji. Vir: Pixabay.

Lokacija masnega središča ni odvisna od referenčnega sistema, ki se uporablja za določitev položajev delcev, saj je lastnost, ki je odvisna od same konfiguracije predmeta in ne od tega, kako je razvidno iz različnih referenčnih okvirjev.

Rešene vaje

- Vaja 1

V mnogih primerih učitelji vsaki ocenjevalni dejavnosti v svojem stolu dodelijo različne uteži ali odstotke. Tako imajo na primer naloge odstotek, druge različne izpite in končni izpit, ki je verjetno veliko večji.

Slika 3. Učitelji v svojih načrtih za ocenjevanje običajno dodelijo različne uteži ocenjevanju. Vir: Knjiga razreda Davida Mulderja prek Flickr.

Recimo, da so pri določenem predmetu ocenjevalne dejavnosti in njihove uteži naslednje:

-Hišne naloge: 20 %

-Kratki izpiti: 25 %

-Laboratorijska poročila: 25 %

-Končni izpit: 30 %

a) Kako učitelj izračuna končno oceno tega predmeta za vsakega učenca?

b) Predpostavimo, da so kvalifikacije določenega študenta na lestvici od 1 do 5, naslednje:

-Naloge: 5.0 točk

-Kratki izpiti: 4.7 točk

-Laboratorijska poročila: 4.2 točki

-Končni izpit: 3.5 točk

Lahko vam služi: Enegon: Lastnosti, kako narediti enegon, primeri

Poiščite končno opombo študenta v tej temi.

Rešitev

a) Vsaka ocena ima drugačno težo, ki jo je učitelj dodelil glede na njihovo zapletenost in lastnimi merili. Na ta način se končna ocena neposredno izračuna kot:

Dokončno = (x20 % naloge + kratki izpiti x25 % + poročila x25 % + končni izpit x30 %) / 100

b) dokončno = (5.0 x 0.2) + (4.7 x 0.25) + (4.2 x 0.25) + (3.5 x 0.3) točke = 4.275 točk ≈ 4.3 točke

- Vaja 2

Lastniki trgovine z oblačili so kupili kavbojke od treh različnih dobaviteljev.

Prva prodana 12 enot po ceni 15 €, drugi 20 enot pri 12.80 € in tretjino kupil veliko od 80 enot pri 11.50 €.

Kakšna je povprečna cena, ki jo plačajo lastniki trgovine za vsakega kavboja?

Rešitev

x_str = (12 x 15 + 20 x 12.80 +80 x 11.50) / (12+20+80) € = 12.11 €

Vrednost vsakega kavboja je 12.11 €, ne glede na to, da nekateri stanejo malo več, drugi pa malo manj. Bilo bi popolnoma enako, če bi lastniki trgovine kupili 112 kavbojk od enega samega dobavitelja, ki bi jih prodal v 12.11 € kos.

Reference

1. Arvelo, a. Ukrepi osrednje težnje. Pridobljeno od: franrarvelo.WordPress.com
2. Mendenhall, w. 1981. Statistični podatki za upravo in ekonomijo. 3. mesto. izdaja. Uredniška skupina Iberoamerica.
3. Moore, d. 2005. Uporabljena osnovna statistika. 2. mesto. Izdaja.
4. Triola, m. 2012. Osnovna statistika. 11. Ed. Pearson Education.
5. Wikipedija. Povprečna teža. Pridobljeno iz: v.Wikipedija.org