Lastnosti ortogonalne matrice, demonstracije, primeri

Ga imate Ortogonalna matrica Ko omenjena matrica, pomnožena s svojim prenosom, ima za posledico matriko identitete. Če je inverzna matrika enaka prenesenemu, je originalna matrica pravokotna.

Ortogonalne matrike so značilne, da je število vrstic enako številu stolpcev. Poleg tega so vektorji vrstic enotni ortogonalni vektorji in tudi izpuščaji prenosnih vektorjev so tudi.

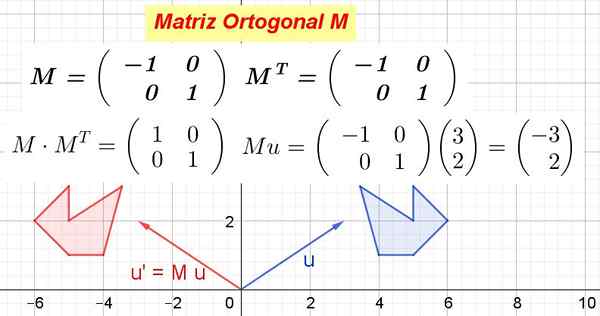Slika 1. Primer ortogonalne matrice in kako preoblikuje geometrijske predmete. (Pripravil Ricardo Pérez)

Ko pravokotna matrika pomnoži vektorji vektorskega prostora Izometrična transformacija, to pomeni preobrazba, ki ne spreminja razdalj in ohranja kote.

Tipičen predstavnik ortogonalnih matric je Rotacijske matrike. Preoblikovanja ortogonalnih matric na vektorskem prostoru se imenujejo Ortogonalne preobrazbe.

Geometrijske transformacije vrtenja in odsev točk, ki jih predstavljajo kartezijanski vektorji. Zaradi tega se ortogonalne matrike pogosto uporabljajo pri računski grafični obdelavi.

[TOC]

Lastnosti

Matrika M Je ortogonalno, če ga pomnoži prenos M^T Rezultat matrike identitete Yo. Podobno je produkt prenosa ortogonalne matrice z izvirno matrico matrice identitete:

M m^T = M^T M = i

Zaradi prejšnje izjave je prenos ortogonalne matrice enak njegovi obratni matriki:

M^T = M^-1.

Nabor pravokotnih matric dimenzij n x n Tvorijo pravokotno skupino Ali (n). In podskupino Ali (n) ortogonalnih matric z določitvijo +1 Posebne matrike skupine (n). Matrice skupine Vaš (n) So matrice, ki proizvajajo linearne rotacijske transformacije, znane tudi kot Skupina rotacij.

Demonstracija

Dokazali bomo, da je matrica pravokotna, če in samo, če so vektorji vrstic (ali vektorjev stolpcev) pravokotni drug do drugega in norme 1.

Vam lahko služi: Bayesovi teorem

Predpostavimo, da so vrste ortogonalne matrice n x n n n ortonormalni vektorji dimenzije n. Če ga označuje v1, v2,.. ., vn N vektorji so izpolnjeni:

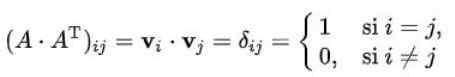
Kjer je očitno, da je niz vektorjev vrstic niz ortogonalnih vektorjev z normo.

Primeri

Primer 1

Pokažite, da je matrika 2 x 2, ki jo ima vektor v svoji prvi vrsti V1= (-1 0) in v svoji drugi vrstici vektor V2= (0 1) je pravokotna matrica.

Rešitev: Matrica je zgrajena M in njegovo prenos se izračuna M^T:

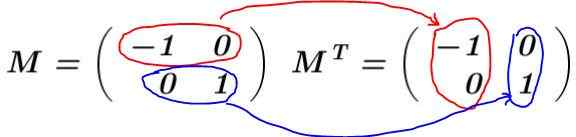
V tem primeru matrika M Gre. Pomnoži M za prenos M^T:

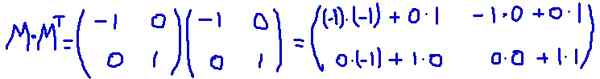
Preverjeno je, da M M^T Je enak matriki identitete:

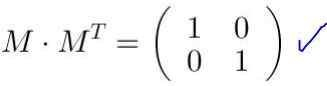
Ko je matrica M Pomnoži se s koordinatami vektorja ali točke, dobimo nove koordinate, ki ustrezajo transformaciji, ki jo matrika naredi na vektorju ali točki.

Slika 1 prikazuje, kako M Preoblikuje vektor ali v ali In tudi všeč M Preoblikujte modri poligon v rdeči poligon. Kot M Je pravokotna, potem je ortogonalna preobrazba, ki ohranja razdalje in kote.

Primer 2

Predpostavimo, da imate v reaisu 2 x 2 matrico, ki je navedena z naslednjim izrazom:

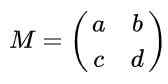
Poiščite resnične vrednosti do, b, c in d tako da matrica M Biti pravokotna matrica.

Rešitev: Po definiciji je matrika pravokotna, če se pomnoži s prenosom kot rezultat, matrika identitete. Če se spomnimo, da je prenesena matrica pridobljena iz izvirnika, je izmenjava vrstic po stolpcih naslednja enakost:

Lahko vam služi: domena in protislovje funkcije (s primeri)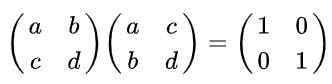

Izvajanje množenja matrice je:

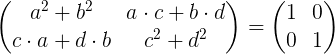
Enako elementov leve matrice z elementi matrike identitete na desni strani dobimo sistem štirih enačb s štirimi neznanimi A, B, C in D.

Za A, B, C in D predlagamo naslednje izraze, ki temeljijo na trigonometričnih razlogih sinus in kosinus:

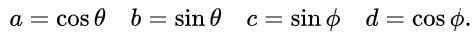
S tem predlogom in zaradi temeljne trigonometrične identitete sta prva in tretja enačba v enakosti matričnih elementov samodejno izpolnjena. Tretja in četrta enačba sta enaka in v matrični enakosti po zamenjavi predlaganih vrednosti je takšna:

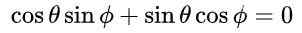
ki vodi do naslednje rešitve:

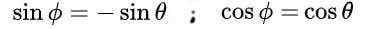
Končno dobimo naslednje rešitve za pravokotno matrico M:

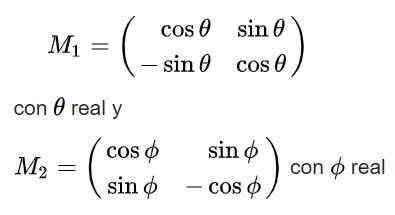
Upoštevajte, da ima prva od rešitev determinant +1, tako da spada v skupino ITS (2), druga rešitev pa determinant -1 in zato ne pripada tej skupini.

Primer 3

Glede na naslednjo matrico poiščite vrednosti A in B, da imata pravokotno matrico.

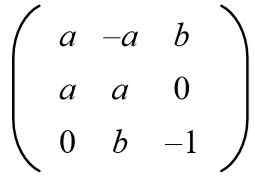
Rešitev: Da bi bila dana matrika pravokotna, mora biti izdelek s prehodom matrica identitete. Nato je narejen matrični produkt matrice, ki je bila dana s prenosno matrico, ki daje naslednji rezultat:

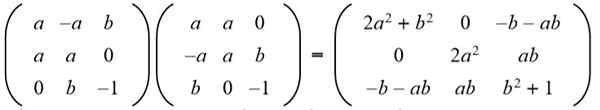
Nato se rezultat ujema z identitetno matrico 3 x 3:

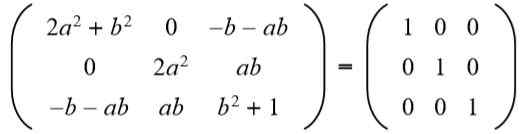
V drugi vrstici tretji stolpec imate (A b = 0), ampak do Ne more biti nič, ker če je tako, enakost elementov druge vrstice in drugega stolpca ne bi bila izpolnjena. Potem nujno B = 0. Zamenjava b Za vrednost 0 imamo:

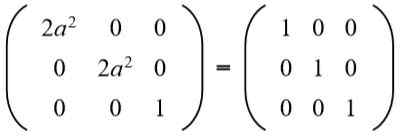
Potem je enačba rešena: 2a^2 = 1, katerih rešitve so: +½√2 in -½√2.

Vam lahko služi: vrste kotov, značilnosti in primerov

Jemanje pozitivne rešitve do Rezultat je naslednja pravokotna matrika:

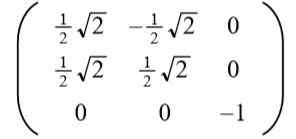
Bralec zlahka preveri, ali so vektorji vrstic (in tudi vektorjev stolpcev) pravokotni in enota, torej ortonormalna.

Primer 4

Dokažite, da je matrica Do katerih vrstice so V1 = (0, -1 0), V2 = (1, 0, 0) in V3 = (0 0 -1) To je pravokotna matrica. Poleg tega poiščite, kako se pretvorijo vektorji kanonične baze I j k Do vektorjev U1, U2 in U3.

Rešitev: Ne pozabite, da je element (i, j) matrice, pomnoženo s prehodom, skalarni produkt vektorja vrstice (i) s stolpcem (j) prenos. Poleg tega je ta izdelek enak delti Kroneckerjeve, če je matrica pravokotna:

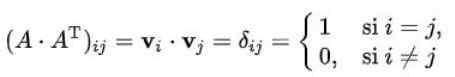
V našem primeru je tako:

V1 • v1 = 0x0 + (-1) x (-1) + 0x0 = 1

V2 • v2 = 1 × 1 + 0x0 + 0x0 = 1

V3 • v3 = 0x0 + 0x0 + (-1) x (-1) = 1

V1 • v2 = 0x1 + (-1) x0 + 0x0 = 0

V2 • v1 = 1 × 0 + 0x (-1) + 0x0 = 0

V2 • v3 = 1 × 0 + 0x (0) + 0x (-1) = 0

V3 • v2 = 0x1 + 0x (0) + (-1) x0 = 0

V1 • v3 = 0x0 + (-1) x (0) + 0x (-1) = 0

V3 • v1 = 0x0 + 0x (-1) + (-1) x0 = 0

S tem, kar je dokazano, da gre za pravokotno matrico.

Poleg tega u1 = a i = (0, 1, 0); U2 = a j = (-1, 0, 0) in končno U3 = a k = (0, 0, -1)

Reference

1. Anthony Nicolaides (1994) Determinants & Matrices. Pass publikacija.
2. Birkhoff in Maclane. (1980). Sodobna algebra, ed. Vicens-Vives, Madrid.
3. Casteleiro Villalba m.  (2004) Uvod v linearno algebro. ESIC uvodnik.
4. Dave Kirkby (2004) Maths Connect. Heinemann.
5. Jenny Olive (1998) Matematika: Vodnik za preživetje študenta. Cambridge University Press.
6. Richard J. Brown (2012) 30-sekundna matematika: 50 najbolj razširjenih teorij v matematiki. Ivy Press Limited.
7. Wikipedija. Ortogonalna matrica. Okrevano od: je.Wikipedija.com
8. Wikipedija. Ortogonalna matrica. Pridobljeno iz: v.Wikipedija.com