Razlaga teorema prekrivanja, aplikacije, rešene vaje

On Teorem superpozicije, V električnih tokokrogih ugotovi, da je napetost med dvema točkama ali tokom skozi njih algebrska vsota napetosti (ali tokov, če je tako) zaradi vsakega vira, kot da vsak deluje v a v a dobro neodvisno.

Ta teorem omogoča analizo linearnih vezij, ki vsebujejo več kot en neodvisni vir, saj je treba samo ločeno izračunati prispevek vsakega.

Linearna odvisnost je odločilna, da se teorem uporabi. Linearno vezje je, da je odziv neposredno sorazmeren.

Na primer, zakon OHM, ki se uporablja za električno odpornost V = i.R, kje V To je napetost, R je odpor in Yo To je tok. Nato je linearna odvisnost od napetosti in toka v uporu.

V linearnih vezjih se uporablja načelo superpozicije ob upoštevanju naslednjega:

-Vsak neodvisni vir napetosti je treba obravnavati ločeno in za to je treba izklopiti vse ostale. Dovolj je, da na 0 v vse tiste, ki niso v analizi, ali jih v shemi nadomestijo s kratkim stikom.

-Če je vir, je treba odpreti vezje.

-Ko upoštevamo notranji upor tako tokov in napetostnih virov, morajo ostati na svojem mestu, saj so del preostalega vezja.

-Če obstajajo odvisni viri, morajo biti tako, kot se pojavlja v vezju.

[TOC]

Prijave

Teorem prekrivanja se uporablja za pridobivanje enostavnejših in lažjih vezij za ravnanje. Vendar je treba upoštevati, da velja samo za tiste z linearnimi odzivi, kot je navedeno na začetku.

Potem ga ni mogoče neposredno uporabiti za izračun moči na primer, saj je moč povezana s tokom do:

P = i² R

Ker je tok kvadrat, odgovor ni linearni. Prav tako ni uporabna za magnetna vezja, v katerih transformatorji posredujejo.

Vam lahko služi: dinamična elektrika

Po drugi strani pa teorem superpozicije ponuja priložnost, da pozna učinek, ki ga ima vsak vir na vezju. In seveda ga je mogoče s svojo uporabo v celoti rešiti, to je poznati tokove in napetosti skozi vsak upor.

Teorem prekrivanja lahko uporabimo tudi v povezavi z drugimi teoremi vezja, na primer Thévenin, za reševanje bolj zapletenih konfiguracij.

V izmeničnem toku je uporaben tudi teorem. V tem primeru sodelujemo z impedancami namesto z upori, dokler lahko izračunamo skupni odziv vsake frekvence neodvisnosti.

Nazadnje je v elektronskih sistemih teorem uporaben tako za neposredno kot za nadomestno analizo toka, ločeno.

Koraki za uporabo teorema o prekrivanju

-Deaktivirajte vse neodvisne vire po navodilih na začetku, razen tiste, ki jo je treba analizirati.

-Določite izhod, bodisi napetost ali tok, ki proizvaja ta en vir.

-Ponovite dva koraka, opisani za vse druge vire.

-Izračunajte algebrsko vsoto vseh prispevkov, ki jih najdemo v prejšnjih korakih.

Rešene vaje

Spodnji primeri razjasnijo uporabo teorema v nekaterih preprostih vezjih.

- Primer 1

V vezju, prikazanem na naslednji sliki, poiščite tok, ki prečka vsak upor skozi teorem prekrivanja.

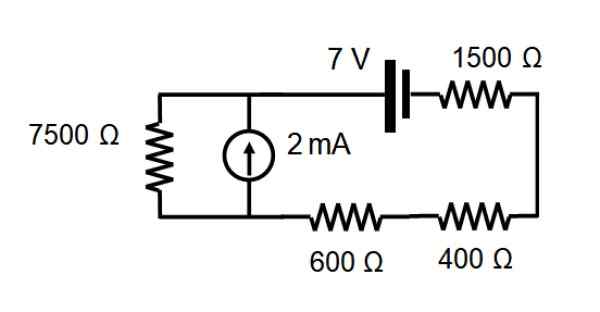
Rešitev

Prispevek vira napetosti

Za zagon trenutnega vira se odpravi, s katerim na ta način ostane vezje:

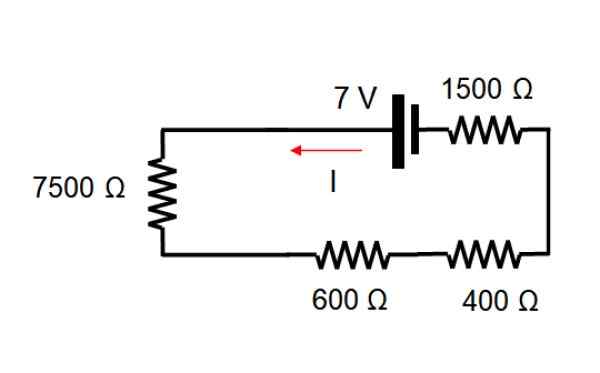
Enakovredna odpornost je dodajanje vrednosti vsakega upora, saj so vsi v seriji:

7500 +600 +400 +1500 Ω = 10.000 Ω

Uporaba Ohmovega zakona V = i.R In čiščenje toka:

I = v / r = 7/10.000 a = 0.0007 a = 0.7 Ma

Ta tok je enak za ves odpor.

Vam lahko služi: Millikan Experiment: postopek, razlaga, pomen

Prispevek trenutnega vira

Vir napetosti se takoj odpravi, da deluje samo s trenutnim virom. Nastalo vezje je prikazano spodaj:

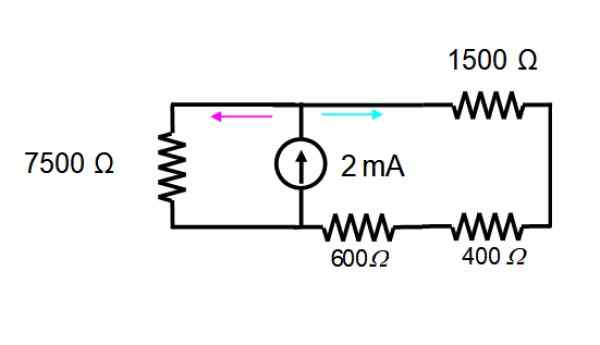
Odpornosti v mreži na desni so serije in jih lahko nadomesti le ena:

600 +400 + 1500 Ω = 2500 Ω

Nastalo vezje je takšno:

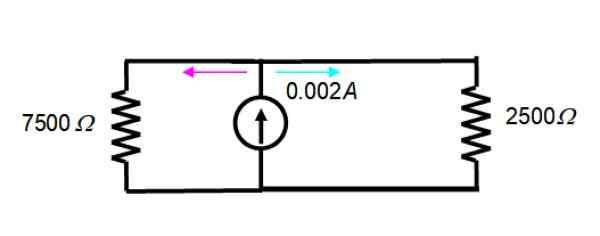
Tok 2 Ma = 0.002 A je razdeljen med dve upori slike, zato je enačba trenutnega delitve veljavna:

Yo_x = (R_Eq/R_x) Yo_T

Kje Yo_x je tok v odpornosti R_x, R_Eq simbolizira enakovredno odpornost in Yo_T je skupni tok. Potrebno je najti enakovredno odpornost med njimi, vedoč, da:

1/r_Eq = (1/ r₁) + (1/ r₂)

Zato:

1/r_Eq = (1/7500) + (1/2500) = 1/1875 → R_Eq = 1875 Ω

Za to drugo vezje tok, ki poteka skozi upor 7500 Ω, nadomešča vrednosti v enačbi toka:

Yo_{7500 Ω} = (1875/7500). 0.002 a = 0.0005 A = 0.5 Ma

Medtem ko je tisti, ki prehaja skozi upor 2500 Ω:

Yo_{2500 Ω} = 2 Ma - 0.5 Ma = 1.5 Ma

Aplikacija teorema Superpozicije

Zdaj se uporablja teorem prekrivanja za vsak upor, začenši s 400 Ω:

Yo_{400 Ω} = 1.5 Ma - 0.7 ma = 0.8 ma

Pomembno: Za to upor se tokovi odštejejo, ko krožijo v nasprotni smeri, kot je razvidno iz skrbnega opazovanja figur, pri katerih imajo čutila tokov različne barve.

Ta isti tok gre enako upornosti 1500 Ω in 600 Ω, saj so vsi v seriji.

Nato se teorem uporabi za iskanje toka skozi upor 7500 Ω:

Yo_{7500 Ω} = 0.7 Ma + 0.5 Ma = 1.2 ma

Pomembno: V primeru upora 7500 Ω opazite, da se tokovi dodajo, ker v obeh vezjih krožijo v isti smeri, ko gredo skozi to upornost. Spet je treba natančno opazovati čutila tokov.

Vam lahko služi: relativna napaka: formule, kako se izračuna, vaje

- Vaja 2

Poiščite tok in napetost skozi upor 12 Ω skozi teorem prekrivanja.

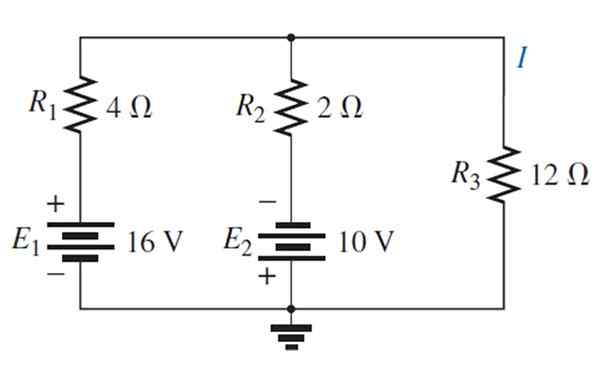
Rešitev

Vir E je zamenjan₁ S kratkim krogom:

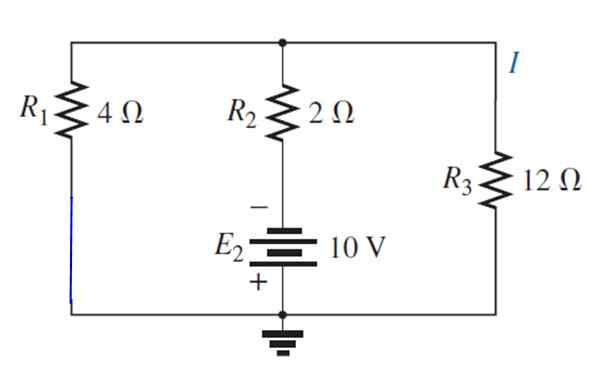
Nastalo vezje je narisano na naslednji način, da se zlahka vizualizirajo upori, ki ostanejo vzporedno:

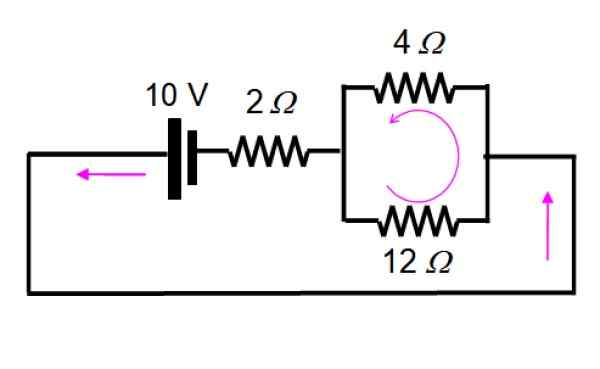
In zdaj je rešena z uporabo serij in vzporednih:

1/r_Eq = (1/12) + (1/4) = 1/3 → R_Eq = 3 Ω

Ta odpor je po drugi strani z upornikom 2 Ω, Zato je skupna odpornost 5 Ω. Skupni tok je:

I = v / r = 10 V / 5 ω = 2 a

Ta tok je razdeljen kot:

Yo_12Ω = (3/12) 2 a = 0.5 a

Zato je napetost:

V_12Ω = 0.5 a × 12 Ω = 6 V

Zdaj je vir aktiviran₁:

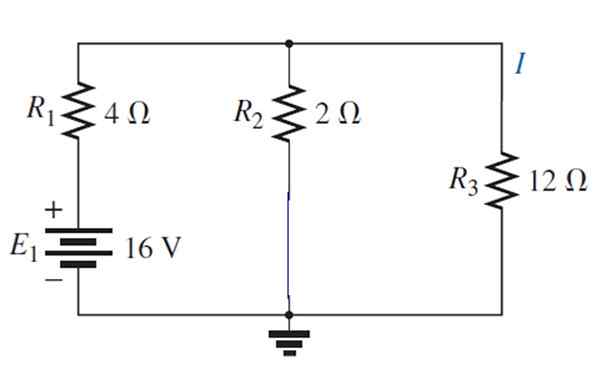
Nastalo vezje je mogoče narisati na ta način:

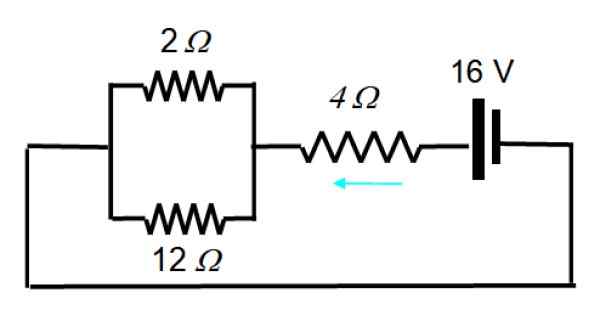
1/r_Eq = (1/12) + (1/2) = 7/12 → R_Eq = 12/7 Ω

In v seriji z 4 Ω To je enakovredna odpornost 40/7 Ω. V tem primeru je skupni tok:

I = v/r = 16 V/(40/7) Ω = 14/5 a

Delilnik napetosti s temi vrednostmi je ponovno uporabljen:

Yo_12Ω = ((12/7)/12) (14/5) a = 0.4 a

Nastali tok je: 0.petdeset.4 a = 0.1 a. Upoštevajte, da so bili odšteti, ker tok vsakega vira daje drugačen pomen, kot je razvidno iz prvotnega vezja.

Napetost skozi upor je:

V_12Ω = 0.4 a × 12 Ω = 4.8 v

Končno je skupna napetost: 6 V-4.8 V = 1.2 v

Reference

1. Aleksander, c. 2006. Temelji električnega vezja. 3. mesto. Izdaja. MC Graw Hill.
2. Boylestad, r. 2011. Uvod v analizo vezja. 2. mesto. Izdaja. Pearson.
3. Dorf, r. 2006. Uvod v električne kroženja. 7. Izdaja. John Wiley & Sons.
4. Edminister, j. Devetnajst devetdeset šest. Električna vezja. Serija Schaum. 3. mesto. Izdaja. MC Graw Hill
5. Wikipedija. Trenutni delitelj. Okrevano od: je.Wikipedija.org.