Matematika

De Morgan zakoni

De Morgan zakoni

Pojasnjujemo, kaj so Morganovi zakoni, jih pokažemo in damo primere

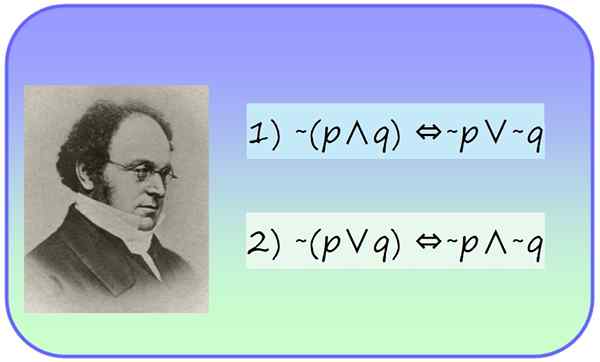Slika 1.- Morganski matematik Augustus (1806-1871) in njegovi zakoni o logiki predloga. Vir: f. Zapata.

Kaj so zakoni De Morgan?

Zakoni De Morgana sta dva logična zakona, ki pripadata logiki predloge, ki jo je oblikoval angleški matematik Augustus iz Morgana (1806-1871). V zvezi z sestavljenim logičnim predlogom vzpostavijo naslednje:

  1. Nasprotno od veznika je enakovredno ločenosti, ki je nastala z nasprotji ali zanikanjem predlogov, ki sestavljajo veznik.
  2. Zavrnitev ločenosti se lahko izrazi kot veznik, ki ga sestavljajo nasprotja ali zanikanja predlogov, vključenih v disjunko.

V zapisu predloge logike so zakoni De Morgan izraženi na kompakten in bolj formalni način:

  1. ∼ (p ∧ q) ⇔ ∼P ∨q
  2. ∼ (p ∨ q) ⇔ ∼P ∧q

Tisti zakoni izražajo, da je bodisi pri zavrnitvi veznika bodisi ločeno, rezultat je enakovreden zanikanju vsakega od sodelujočih predlogov ločeno in vlaganje priključka, ki jih povezuje.

Za boljše razumevanje zakonov De Morgana je treba pregledati pomen predlogov in simbolov, ki se uporabljajo v logiki predloga.

Logična zapis

Osnovno orodje predloga logike so predloge. Logična predlog je izjava, ki prizna resnična vrednost, Ali je resnično ali napačno, ne pa oboje hkrati. V tem dvoumnosti ni dovoljeno, to je nedvomno.

Predlog je označen z malimi črkami, kot v naslednjih primerih:

  • V: Mexico City je glavno mesto Mehike (resnično).
  • V: Z dodajanjem 2 in 3, 4 (false) dobimo.
  • O: Vsi sesalci so kopenske živali (lažne).
Vam lahko služi: Heptagon

Obstajajo tudi bolj zapleteni predlogi, ki so strukturirani z uporabo preprostih predlogov, kot so ta:

  • V: Carlos bo šel v kino, če ne bo deževalo.
  • V: ANA je kemik ali morski biolog.
  • O: Juan gre na večerjo ali Pedro si bo ogledal igro na televiziji.

Logični konektorji

Logični konektorji so simboli, ki se uporabljajo za povezovanje preprostih predlogov in tako gradijo bolj zapletene predloge. V predlogirani logiki ima vsak od njih poseben pomen.

Najbolj uporabljeni konektorji so povezava, disjunkcija, ekskluzivna ločitev, zanikanje, pogojnost in dvo-kondicioniranost.

Veznik

Povezava je označena z obrnjenim pismom "V". Kompozitni predlog skozi konjunkcijo je simbolizirano p ∧ q, kot sledi:

  • P ∧ Q: Mexico City je glavno mesto Mehike in je v Severni Ameriki.

Tukaj je enostavno ugotoviti, da je P "Mexico City glavno mesto Mehike" in Q je "v Severni Ameriki".

Disjunkcija

Razlikujejo dve vrsti disjuncije: šibka in ekskluzivna. A šibka ločitev Simbolizira ga ∨ in v logičnem zapisu bi bil p ∨ q. Primer tovrstne disjuncije je:

  • P ∨ Q: Juan je nogometaš ali je Juan teniški igralec.

Namesto tega ekskluzivna disjunkcija Simbolizira se z znakom ⊻ in pomeni, da je treba na primer izključiti eno od predlogov:

P ⊻ Q: Alicia je stara 20 let ali Alicia je stara 22 let.

Razlika med obema vrstama je jasna, v ekskluzivni ločitvi je ena od predlogov izključena, saj če je Alicia star 20 let, ne more biti 22 in obratno. Po drugi strani pa je Juan v šibki disjunciji hkrati lahko nogometaš in teniški igralec.

Zanikanje

Z vložitvijo simbola ∼ Predlog je to zavrnjeno, kot v:

  • V: ∼ (Veracruz je prestolnica Mehike).

To se bere kot "Veracruz ni glavno mesto Mehike". Drugi načini izražanja zanikanja, razen "ne", so s stavki, kot so "lažni", "je laž, ki" in "ni res, da".

Vam lahko služi: linearna interpolacija

Pogoj

Gre za sestavljene predloge, ki običajno uporabljajo besedi "da" in "potem ...", da povežejo dve predlogi, v katerih obstaja pogojnost oz posledice. Del predloga, ki je zapisan takoj po "da" je antecedent val hipoteza predloga in kaj je po izrazu "potem je" zaključek tudi posledično.

Simbol, ki se uporablja za pogojnost, je puščica od leve proti desni "→", zato je pogoj med dvema predlogoma predstavljena kot P → Q, ki se lahko prebere kot "Če je P, potem Q". Na primer:

P → V: Če bo popoldne deževalo, potem ne bom igral tenisa.

Dvo-kondicioniranje

Pri tej vrsti predloga se uporablja stavek "da in samo, če" za povezovanje dveh predlogov, imenovanih prvi in ​​drugi dvokostni član. Uporabljeni simbol je dvosmerna puščica "↔".

Oba predloga, povezana z "da, in samo, če" se imenujeta najprej in drugi član in dvo-kondicionalnost dveh predlogov P in Q ostaja kot p ↔ q. Na primer:

P ↔ Q: Marija rada vozi s kolesom, če in samo, če je dan sončen.

Demonstracija zakonov De Morgana

Zakoni De Morgana so del logičnih enakovrednosti in jih je mogoče dokazati s tabelami resnice, ki se uporabljajo za poznavanje resnice (resnične ali napačne) vrednosti predloga.

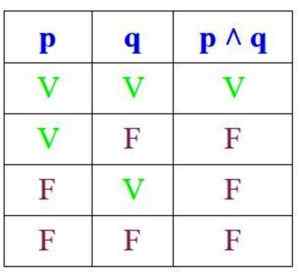
Ker je konjunkcija resnična le, kadar sta P in Q resnični, je njegova tabela resnice:

Po drugi strani pa je v disjunciji ta predlog resničen, če sta p in q resnična ali če je vsaj eden od njih, vendar je napačno, če sta oboje:

Vam lahko služi: permutacije brez ponovitve: formule, demonstracije, vaje, primeri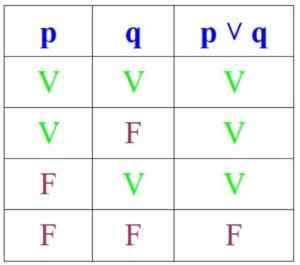

Zdaj zanikanje resnico spremeni v lažno in obratno. V tem primeru so vrednosti resnice ∼ (p ∧ q) in ∼ (p ∨ q) nasprotno od vrednosti resnice (p ∧ q) in (p ∨ q):

In preveriti je treba, da se ti rezultati pridobijo pri izvajanju ustreznih tabel resnice (∼ P ˅ ∼ Q) in (∼ P ˄ ∼ Q):

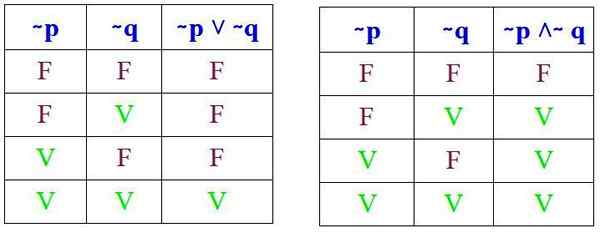
In v resnici pri primerjavi ustreznih tabel resnice opažamo, da so zakoni De Morgan izpolnjeni. Zdaj bosta vidna dva primera njene prijave.

Rešen primer 1

Uporabite zakone De Morgan, da najdete enakovreden izraz: ∼ (∼P ˅ ∼Q)

  • Rešitev

Dani izraz primerjamo ∼ (∼P ˅ ∼Q) z Morganovim zakonom:

∼ (p ∨ q) ⇔ ∼P ∧q

In opazimo, da je zanikanje že zunaj oklepaja v obeh primerih, zato se upoštevajo navodila zakona: zavrne ∼P, zanika ∼Q in se priključek spremeni:

∼ (∼P ˅ ∼Q) ⇔ ∼ (∼P) ∧ ∼ (∼Q) ⇔ p ∧ q

Rešen primer 2

Določite enakovredni izraz ∼ [∼P ˄ ∼ (∼Q)] ≡

  • Rešitev

Prvič, zanikanje ∼Q je poenostavljeno:

∼ [∼P ˄ ∼ (∼Q)] ⇔ ∼ [∼P ˄ q]

Ker je zunaj nosilca že zanikanje, se dobljeni izraz primerja z Morganovim zakonom: ∼ (p ∧ q) ⇔ ∼P ∨q

Če želite rešiti ∼ [∼P ˄ Q], morate zanikati ∼P, zavrniti Q in spremeniti priključek:

∼ [∼P ˄ Q] ⇔∼ (∼P) ∨ ∼Q ⇔ P ˅ ˅ ∼Q

Reference

  1. Becerra, j.M.  Unam Logic Notes.
  2. Briljantno. Iz Morganovih zakonov. Okreval od: briljantno.org.
  3. Vadnice za elektroniko. Po Morganovi teoremu. Okrevano od: elektronike-tormales.Ws.
  4. López, f. Uvod v matematično logiko. Obnovil od: YouTube.com
  5. Muñoz, c. Uvod v logiko. Pridobljeno iz: spletnih mest.UCM.je.