BIOT-SAVART LAZNI FORMURA, PREDSTAVITEV

The Zakon o Biot-Savart vzpostavi razmerje med magnetnim poljem DB  na točki P, ki jo proizvaja tanka žica, ki prevaža tok I in katerih diferencialna dolžina je Ds. Ta zakon se uporablja za iskanje magnetnega polja trenutnih distribucij prek Načelo superpozicije. 

To pomeni, da moramo za izračun skupnega magnetnega polja v točki P dodati vse prispevke, ki jih vsak diferencialni del Ds žice prispeva. In ta vsota se izvede prek integrala, ki se izvaja v celotni porazdelitvi toka.

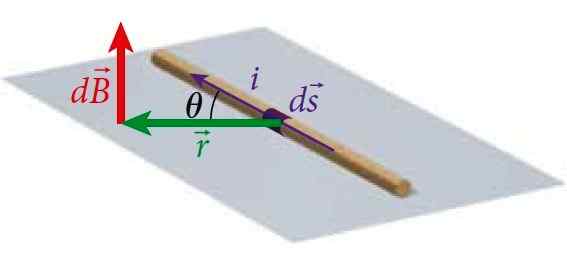
Slika 1. Žični segment prevaža tok I, ki proizvaja magnetno polje v točki P na določeni razdalji od žice, ki ga izračuna zakon o Biot-Savart. Vir: Bauer, W. Fizika za inženiring in znanosti.

Na ta način lahko izračunate polje, ki proizvaja žice s tokom različnih geometrij.

Zakon Biot-Savart je poimenovan po dveh francoskih fizikih, ki sta ga odkrila leta 1820: Jean Marie Biot (1774-1862) in Felix Savart (1791-1841). Da bi to dosegli, so morali preučiti intenzivnost in obliko magnetnega polja, ki ga povzročajo številne porazdelitve tokov.

[TOC]

Formula

Matematični izraz zakona o Biot-Savart je naslednji:

Ohranja analogije z enakovrednim za izračun električnega polja: Coulombov zakon, le da je magnetno polje DB v P je pravokotno do letala, kjer se nahaja žica. To lahko vidimo na sliki 1.

Prejšnji izraz lahko zapišemo tudi na naslednji način:

V obeh izrazih, r Je vektor položaja, usmerjen iz toka ID -jas do točke, ko želite izračunati polje.

Vam lahko služi: ohranjanje linearnega zagona: načelo, primeri, vaje.

S svojim delom, r Z naglasom Circusflejo je enotni vektor, ki je usmerjen v isto smer in smer, vendar z modulom, ki je enak 1. Vektor r Predstavljen je na naslednji način:

Zaradi tega z zamenjavo v prejšnji enačbi -tistega, ki ima r³ V imenovalcu- izraz r je takoj dosežen² V imenovalniku.

Poleg zgoraj omenjenih vektorjev formula vsebuje konstanto μ_tudi, KLIČITE Vakuumska prepustnost in čigar vrednost je:

μ_tudi = 4π x10^-7 T.m/ a.

Če želimo izračunati vektor magnetnega polja, je treba integrirati vso trenutno porazdelitev, za katero potrebujemo podatke o njegovi geometriji:

Vektorski izdelek in pravilo desne roke

Zakon o Biot-Savart vključuje vektorski izdelek med vektorji IDs in r. Rezultat vektorskega izdelka med dvema vektorjem je tudi vektor.

V tem primeru modul ID vektorskega izdelkas x r IS: (IDS) ⋅R⋅senθ, kjer je θ kot med IDs in r, kot je prikazano na sliki 1.

Na ta način je velikost polja DB Daje ga:

Smer in pomen je mogoče določiti s pravilom desne roke, kar je prikazano na tej sliki:

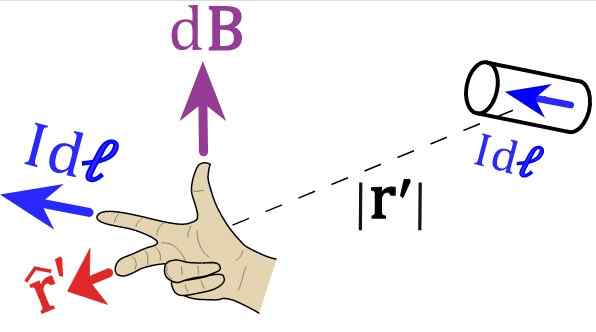Slika 2. Pravilo desnega roka za zakon o bit-Savart. Vir: Wikimedia Commons.

Bralca povabimo, da postavi desno roko po vektorjih slik 1 in 2. Za sliko 1 mora kazalec kazalec usmeriti v levo, po ID -jus ali idl, Srednji prstni točke glede na vektor r enotna.

In končno je palec usmerjen in to je smer magnetnega polja.

Vam lahko služi: elipsoid: značilnosti in primeri

Demonstracija zakona o Biot-Savart

Zakon o Biot-Savart je izjemno eksperimentalno, kar pomeni, da njegova formulacija izvira iz številnih opažanj o obnašanju magnetnega polja, ki ga proizvajajo trenutne žice.

Opazovanja biot in savart

To so bila opažanja francoskih znanstvenikov o magnetnem polju DB:

-Velikost dB je obratno sorazmerno r².

-Prav tako je neposredno sorazmerna z velikostjo trenutnega elementa, ki se imenuje IDs In tudi do sena θ, kjer je θ kot med vektorji ds in r.

-dB je pravokotno na obe IDs -smer toka r.

-Raznoliko dB je tangencialna za radijski krog r Žica -cent. Z drugimi besedami, polje B, ki ga ustvari trenutni segment, je sestavljeno iz koncentričnih okoliščin za neplodne.

-Pomen, v katerem se vrti B Daje ga pravi pravilo: desni palec je usmerjen v smer toka, preostali štirje prsti.

Vsa ta opažanja so združena v matematičnem izražanju predhodno opisanega zakona.

Prijave za zakonodajo Biot-Savart

Ko ima trenutna porazdelitev visoko simetrijo, je mogoče enostavno rešiti integral, poglejmo nekaj primerov:

Pravokotna in tanka žica

Praktilinearna žica dolžine L prevaža tok I, kot je tisti, ki se pojavi na sliki.

Ponazarja potrebno geometrijo za izračun polja. To je pravokotno na list papirja, odhaja do ravnine, če tok teče od leve proti desni, in drugače (preverite s pravilom desne roke).

Vam lahko služi: paramagnetizem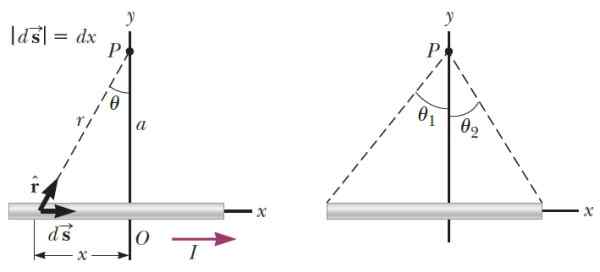Slika 3.- Na levi strani je geometrija, potrebna za izračun magnetnega polja, ki proizvaja tanek žični segment v točki P. Na desni koti, ki določajo položaj P glede na konce segmenta. Vir: Serway, r. Fizika za znanost in inženiring.

Biti k  Enotni vektor v smeri, pravokoten na ravnino, po izvedbi procesa integracije je magnetno polje, ki ga žice proizvaja v p,::

Krožna spira

Radijska krožna zanka do Prevaža tok, kot je prikazano na sliki, in ustvari magnetno polje DB -V temno zeleni točki P na osni osi, na daljavo x iz centra.

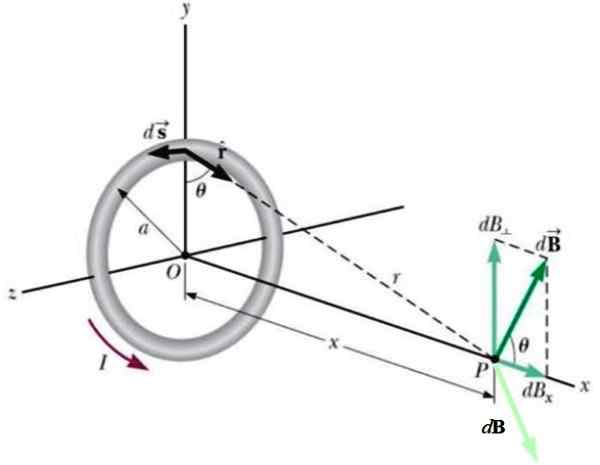Slika 4.- Geometrija za izračun polja, ki ga proizvaja krožna lopatica v točki P na osni osi. Vir: Wikimedia Commons.

Drug trenutni element, ki se nahaja na nasprotni strani, bi prispeval še en prispevek k DB (svetlo zelena), tako da je navpična komponenta preklicana s prvim.

Rezultat tega je, da je neto magnetno polje vodoravno, zato je vključeno le v te komponente, kar ima za posledico:

Vaja rešena

Obstaja izjemno dolga žica, ki prenaša tok 2 za pretok, kot je prikazano na sliki. Izračunajte velikost magnetnega polja na radialni razdalji 5 cm od žice.

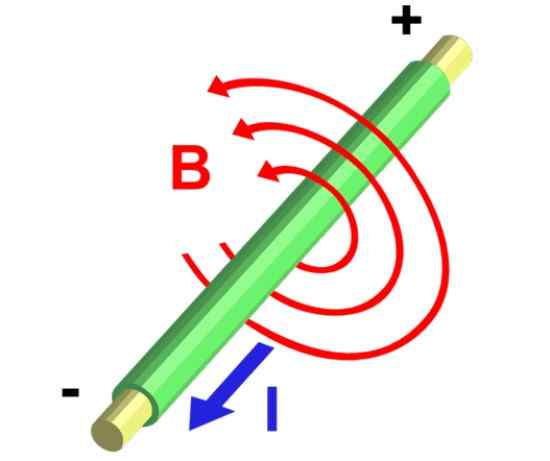Slika 5.- Magnetne poljske črte pravokotnega žičnega segmenta, ki prevaža tok. Vir: Wikimedia Commons.

Rešitev

Ker gre za zelo dolgo žico, lahko vzamemo izraz za pravokotni segment in naredimo θ₁= 0 ° in θ₂ = 180 ° za omejene kote. To je dovolj, da dolžina žice shrani neskončnost.

Na ta način bomo imeli polje:

Ki poenostavi:

Zdaj nadomestimo vrednosti izjave:

I = 2 a

R = 5 x10^-2 m

μ_tudi= 4π x10^-7 T.m/ a

Smer in občutek B Prikazani so na sliki 5, kjer je bila smer, ki zapusti list k.

Reference

1. Bauer, w. 2011. Fizika za inženiring in znanosti. Zvezek 1. MC Graw Hill.
2. Figueroa, d. 2005. Serija: Fizika za znanost in inženiring. Zvezek 6. Elektromagnetizem. Uredil Douglas Figueroa (USB).
3. Giancoli, d.  2006. Fizika: načela z aplikacijami. 6. Ed Prentice Hall.
4. Resnick, r. 1999. Fizično. Vol. 1. 3. izd. v španščini. Continental uredništvo s.Do. od c.V.
5. Sears, Zemansky. 2016. Univerzitetna fizika s sodobno fiziko. 14. Ed. Zvezek 1.
6. Serway, r., Jewett, J. 2008. Fizika za znanost in inženiring. Zvezek 2. 7. Ed. Cengage učenje.